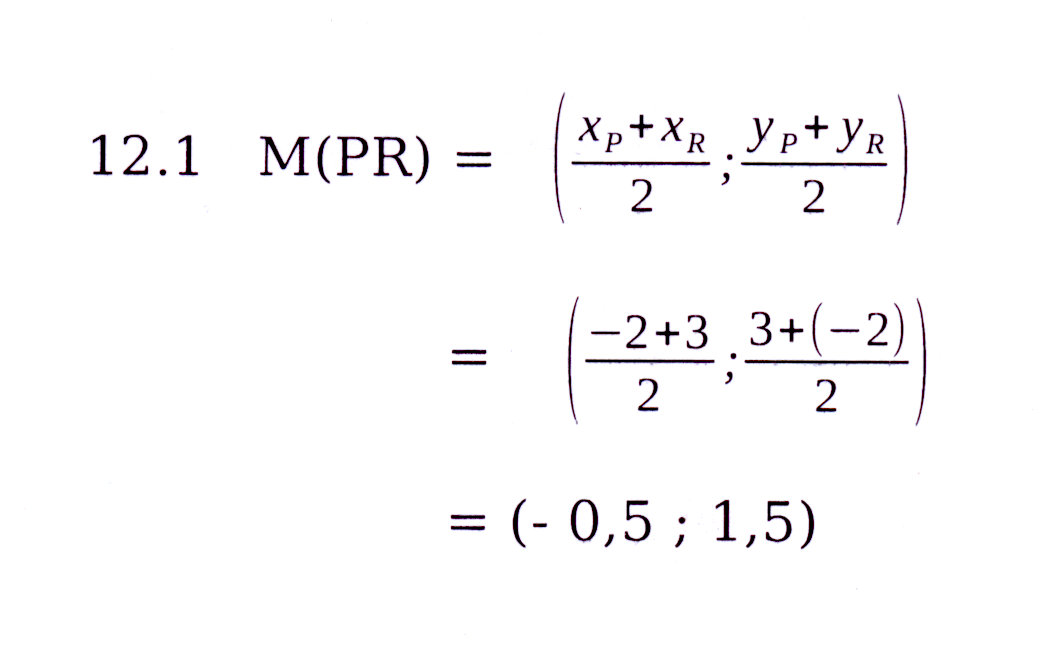WISKUNDE
GRAAD 10
NOG OEFENINGE
Toepassings : antwoorde.To
GRAAD 10
NOG OEFENINGE
Toepassings : antwoorde.To
MATHEMATICS
GRADE 10
MORE EXERCISES
Applications : answers.
GRADE 10
MORE EXERCISES
Applications : answers.
—————————————
1.1 d(AB) = √((xB − xA)2 + (yB − yA)2)
—————————————
= √((1 − (−5)2 + (−1 − 5)2)
—————
= √36 + 36
——
= √72 = 8,49
yB − yA −1 − 5
1.3 m(AB) = ────── = ──────
xB − xA 1 − (−5)
−6
= ── = −1
6
m(AB) × m(CD) = −1 × 1
= −1
∴ AB ⊥ CD
yD − yC 2 − 7
m(CD) = ────── = ──────
xD − xC −2 − 3
−5
= ─── = 1
−5
—————————————
1.4 d(AC) = √((xC − xA)2 + (yC − yA)2)
—————————————
= √((3 − (−5))2 + (7 − 5)2)
————— ——
= √64 + 4 = √68
∴ AC = BC en dus / and therefore
ΔABC is 'n gelykbeninge driehoek.
ΔABC is an isosceles triangle.
—————————————
1.5 d(AB) = √((xB − xA)2 + (yB − yA)2)
—————————————
= √((3 − 1)2 + (7 − (−1))2)
————— ——
= √4 + 64 = √68
—————————————
2.1.2 d(AB) = √((xB − xA)2 + (yB − yA)2)
—————————————
= √((−7 − (−3))2 + (5 − (−2))2
————— ——
= √16 + 49 = √65
2.2 M is die middelpunt van BC. A en M het
dieselfde x-koördinate sodat AM // Y-as.
Net so, BC // X-as en dus AM ⊥ BC
Dus, AM is die middelloodlyn van BC.
M is the midpoint of BC. A and M have the
same x-coordinate so that AM // Y-axis.
Similarly, BC // X-axis and thus AM ⊥ BC
Thus, AM is the perpendicular bisector of BC.
———————————
2.3 d(AC) = √((1 − (−3))2 + (−2 − 5)2
————— ——
= √(16 + 49) = √65
AB = AC en dus is ∠ABC = ∠ACB.
Vr. / Qu. 2.3
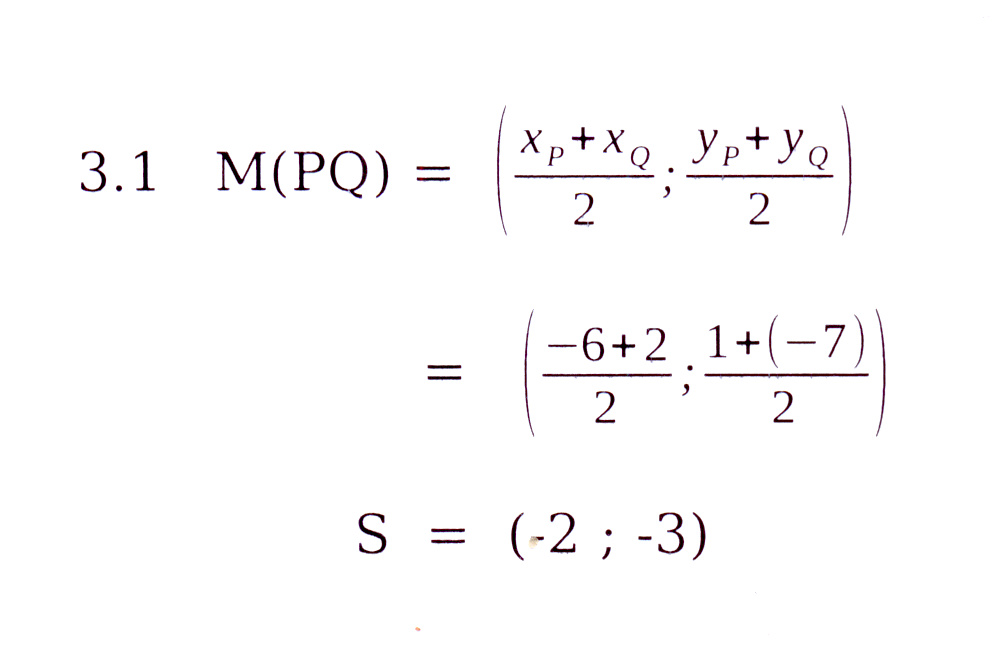
−7 − (−1) −6
3.3 m(RQ) = ────────= ───
2 − 8 −6
= 1
y Q − yP −7 − 1
3.4 m(PQ) = ─────── = ──────
xQ − xP 2 − (−6)
− 8
= ── = −1
8
m(PQ) × m(RQ) = −1 × 1 = −1
∴ PQ ⊥ RQ en ΔPQR is 'n reghoekige driehoek.
∴ PQ ⊥ RQ and ΔPQR is a rightangled triangle.
3.2 Mediaan halveer teenoorstaande sy. /
Median bisects opposite side.
S is the midpoint. / die middelpunt.
yS − yR −3 − (−1)
m(RS) = ───── = ──────
xS − xR −2 − 8
−2
= ─── = 0,2
−10
By / At R : y − yR = m(x − xR)
1
y − (−1) = ── (x − 8)
5
1 13
y = ── x − ──
5 5
OF / OR x − 5y − 13 = 0
yL − yK yM − yL yM − yK
m(KL) = ─────── m(LM) = ─────── m(KM) = ───────
xL − xK xM − xL xM − xK
−5 − 9 −1 − (−5) −1 − 9
= ─────── = ─────── = ───────
−5 − 2 −13 − (−5) −13 − 2
− 14 4 1 − 10 2
= ──── = 2 = ──── = − ── = ──── = − ──
−7 −8 2 −15 3
m(KL) × m(LM) = 2 × −0,5 = − 1
∴ KL ⊥ LM sodat ∠KLM = 90° en ΔKLM 'n reghoekige driehoek is. /
∴ KL ⊥ LM so that ∠KLM = 90° and ΔKLM is a right-angled triangle.
Bereken die gradiënte van die sye DE en EF
om aan te toon dat DE⊥EF en dus is ∠DEF = 90°.
yE − yD 5 − 9
m(DE) = ─────── = ───────
xE − xD −3 − 5
− 4 1
= ─── = ──
− 2 2
1
m(DE) × m(EF) = ── × −2
2
= − 1
Calculate the gradients of sides DE and EF
to show that DE⊥EF and thus ∠DEF = 90°.
yF − yE 1 − 5
m(EF) = ─────── = ───────
xF − xE −1 − (−3)
− 4
= ── = −2
2
∴ KL ⊥ LM sodat ∠KLM = 90° en ΔKLM 'n reghoekige driehoek is. /
∴ KL ⊥ LM so that ∠KLM = 90° and ΔKLM is a right-angled triangle.
Vraag / Question 5.
∴ KL ⊥ LM so that ∠KLM = 90° and ΔKLM is a right-angled triangle.
Bereken die lengte van elke sy om te bepaal watter twee sye ewe lank is. /
Calculate the length of each side to determine which two sides have the same length.
────────────── ────────────── ──────────────
d(AB) = √ (xB − xA)2 + (yB − yA)2 d(BC) = √ (xC − xB)2 + (yC − yB)2 d(AC) = √ (xC − xA)2 + (yC − yA)2
──────────────── ───────────────── ─────────────────
= √ (1 − (−6))2 + (−3 − 7)2 = √ (−9 − 1)2 + (−10 − (−3))2 = √ (−9 − (−6))2 + (−10 − 7)2
──────── ──── ──────── ─── ──────── ────
= √ (49 + 100) = √ 149 = √ (100 + 49) = √ 149 = √ (9 + 289) = √ 298
d(AB) = d(BC) en dus is ΔABC 'n gelykbenige driehoek. / and therefore ΔABC is an isosceles triangle.
As ∠QPR = ∠PRQ, dan moet QP = QR. Bereken
dus die lengte van hierdie twee sye.
—————————————
d(QP) = √((xP − xQ)2 + (y − yQ)2)
—————————————
= √((−3 − (−7))2 + (−2 − 7))2
————— ——
= √16 + 81 = √97
QP = QR en dus is ∠QPR = ∠PRQ.
If ∠QPR = ∠PRQ, then QP must be equal
to QR. Calculate the lenghts of these two sides.
—————————————
d(QR) = √((xR − xQ)2 + (yR − yQ)2)
—————————————
= √((2 − (−7))2 + (3 − 7)2)
————— ——
= √81 + 16 = √97
QP = QR and thus ∠QPR = ∠PRQ.
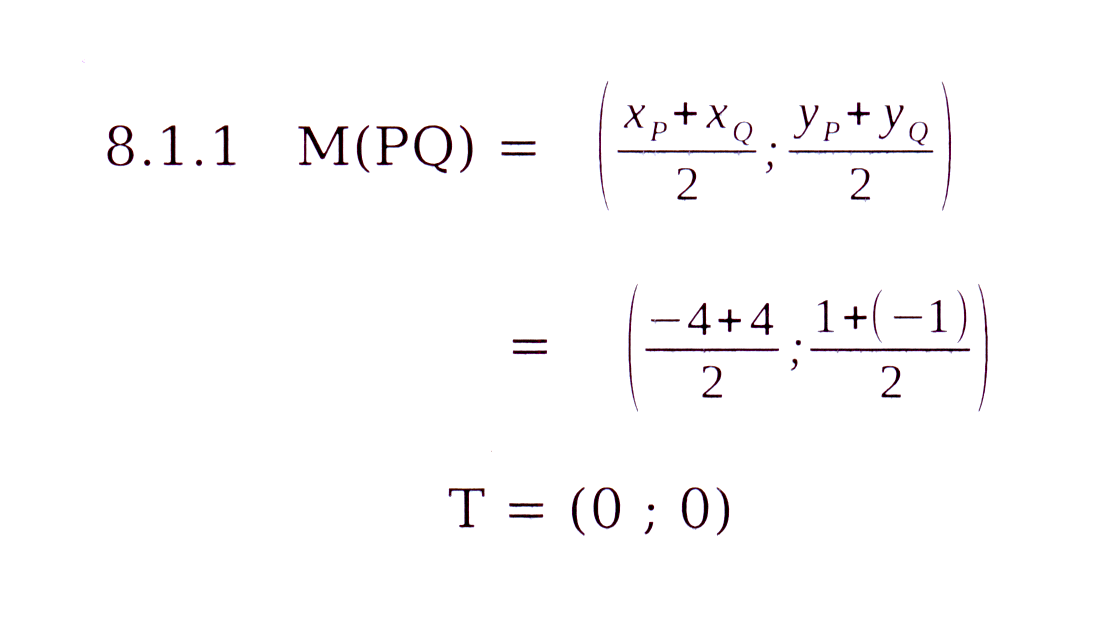
yR − yP −8 − 1
8.1.3 m(PR) = ─────── = ───────
xR − xP 5 − (−4)
− 9
= ─── = −1
9
8.3 Oppervlakte van ΔPQR = ½bh. Bereken dus
die lengtes van QS en PR.
—————————————
d(QS) = √((xS − xQ)2 + (yS − yQ)2)
—————————————
= √((1 − 4)2 + (−4 − (−1))2)
——— ——
= √9 + 9 = √18
Oppervlakte / Area ΔPQR = 0,5 × b × h
—— ——
= 0,5 × √18 × √162
= 27 eenhede2 / units2
yS − yR −4 − (−8)
8.1.2 m(RS) = ─────── = ───────
xS − xR 1 − 5
4
= ─── = −1
−4
By / At R : y − yR = m(x − xR)
y − (−8) = −1(x − 5)
y = −x − 3
yS − yQ −4 − (−1)
8.2 m(QS) = ─────── = ───────
xS − xQ 1 − 4
−3
= ─── = 1
−3
m(QS) × m(PR) = 1 × − 1 = −1
∴ QS ⊥ PR
Area of ΔPQR = ½bh. Thus, calculate the
lengths of QS and PR.
—————————————
d(PR) = √((xR − xP)2 + (yR − yP)2)
—————————————
= √((5 − (−4))2 + (−6 − 1)2 )
————— ——
= √81 + 81 = √162
9.1 CD ⊥ AB as / if m(CD) × m(AB) = −1
yD − yC 1 − (−2)
m(CD) = ─────── = ───────
xD − xC −3 − 3
3 1
= ─── = − ──
−6 2
1
m(CD) × m(AB) = − ── × 2
2
= −1
∴ CD ⊥ AB
Die swaartelyn / mediaan van B na AC halveer AC.
Bereken dus die koördinate van P, die middelpunt
van AC.
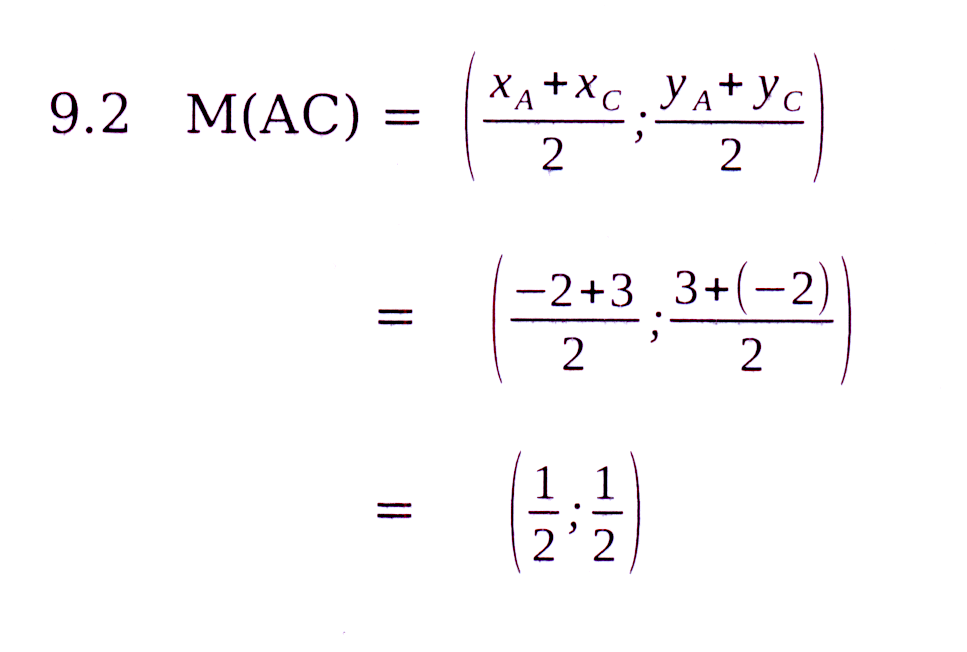
By / At B : y − yB = m( x − xB )
1
y − (−1) = ── ( x − (−4))
3
1 1
y = ── x + ── OF / OR 3y = x + 1
3 3
The median from B to AC bisects AC.
Thus, calculate the coordinates of P, the midpoint of AC.
Bereken die gradiënt van BP. /
Calculate the gradient of BP.
yP − yB 0,5 − (−1)
m(BP) = ─────── = ───────
xP − xB 0,5 − (−4)
1,5 1
= ─── = ──
4,5 3
9.3 CD ⊥ AB . . . (9.1) en
die oppervlakte van ΔABC = 0,5 × AB × CD.
Bereken dus die lengtes van AB en CD.
—————————————
d(AB) = √((xB − xA)2 + (yB − yA)2)
—————————————
= √((−4 − (−2))2 + (−1 − 3)2 )
———— ——
= √4 + 16 = √20
Oppervlakte / Area ΔABC = 0,5 × b × h
—— ——
= 0,5 × √20 × √45
= 15 eenhede2 / units2
CD ⊥ AB . . . (9.1) and
the area of ΔABC = 0,5 × AB × CD.
Therefore, calculate the lengths of AB and CD.
—————————————
d(CD) = √((xD − xC)2 + (yD − yC)2)
—————————————
= √((3 − (−3))2 + (−2 − 1)2 )
————— ——
= √36 + 9 = √145
yB − yA 1 − 4
10.1 m(AB) = ─────── = ───────
xB − xA −4 − (−1)
−3
= ─── = 1
−3
m(AB) = m(CD) en dus / and therefore AB || CD
yD − yC 1 − (−2)
m(CD) = ─────── = ───────
xD − xC 2 − (−1)
3
= ─── = 1
3
—————————————
10.2 d(AB) = √((xB − xA)2 + (yB − yA)2)
—————————————
= √((−4 − (−1))2 + (1 − 4)2 )
——— ——
= √9 + 9 = √18
d(AB) = d(CD) en dus / and therefore AB = CD
—————————————
d(CD) = √((xD − xC)2 + (yD − yC)2)
—————————————
= √((2 − (−1))2 + (1 − (−2))2 )
——— ——
= √9 + 9 = √18
yC − yB −2 − 1
10.3 m(BC) = ─────── = ───────
xC − xB −1 − (−4)
−3
= ─── = −1
3
m(AB) × m(BC) = 1 × −1
= −1
∴ AB ⊥ BC sodat / so that ∠ABC = 90°
—————————————
10.4 d(BC) = √((xC − xB)2 + (yC − yB)2)
—————————————
= √((−1 − (−4))2 + (−2 − 1)2 )
——— ——
= √9 + 9 = √18
∴ AB = BC = CD en / and ∠ABC = 90°
sodat / so that
ABCD 'n vierkant is. / is a square.
yN − yK 3 − 5
11.1 m(KN) = ─────── = ───────
xN − xK 3 − 1
−2
= ─── = −1
2
m(KN) = m(LM) sodat / so that KN || LM
yM − yL −3 − (−1)
m(LM) = ─────── = ───────
xM − xL −1 − (−3)
−2
= ─── = −1
2
—————————————
11.2 d(KN) = √((xN − xK)2 + (yN − yK)2)
—————————————
= √((3 − 1)2 + (3 − 5)2 )
——— —
= √4 + 4 = √8
d(KN) = d(LM) en dus / and therefore KN = LN.
—————————————
d(LM) = √((xM − xL)2 + (yM − yL)2)
—————————————
= √((−1 − (−3))2 + (−3 − (−1))2 )
——— —
= √4 + 4 = √8
11.3 KN = LM en KN || LM sodat
KLMN 'n parallelogram is.
KLMN is 'n reghoek as enige hoek, en
dus al vier hoeke, 'n regte hoek is.
Bepaal of enige hoek bv. ∠KLM 'n
regte hoek is. Is KL ⊥ LM?
yL − yK −1 − 5
m(KL) = ─────── = ───────
xL − xK −3 − 1
−6
= ─── = 1,5
−4
m(KL) × m(LM) = 1,5 × −1 = −1,5 ≠ −1
KN = LM and KN || LM so that
KLMN is a parallelogram.
KLMN is a rectangle if any angle, and
therefore all four angles, is a right angle.
Determine whether any angle, say
∠KLM is a right angle. Is KL ⊥ LM?
yM − yL −3 − (−1)
m(LM) = ─────── = ───────
xM − xL −1 − (−3)
−2
= ─── = −1
2
—————————————
12.2 d(QM) = √((xM − xQ)2 + (yM − yQ)2)
—————————————
= √((−0,5 − (−4))2 + (1,5 − 1)2 )
——— —
= √4 12,25 + 0,25 = √12,5
—————————————
d(MS) = √((xS − xM)2 + (yS − yM)2)
—————————————
= √((3 − (−0,5))2 + (32 − 1,5)2 )
——— —
= √12,25 + 0,25 = √12,5
d(QM) = d(MS) en dus / and therefore QM = MS.
yR − yQ −2 − 1
12.3 m(QR) = ─────── = ───────
xR − xQ −3 − (−4)
−3
= ─── = −3
1
2
m(QR) × m(RS) = −3 × ── = −2 ≠ −1
3
∴ ∠QRS ≠ 90°
yS − yR 2 − (−2)
m(RS) = ─────── = ───────
xS − xR 3 − (−3)
4 2
= ─── = ──
6 3
12.4 M is die middelpunt van PR (12.1) en
QM = MS (12.2)
sodat PQRS 'n parallelogram is want die
hoeklyne halveer mekaar in M.
∠QRS ≠ 90° (12.3) en dus is
PQRS nie 'n reghoek nie.
M is the midpoint of PR (12.1) and
QM = MS (12.2)
so that PQRS is a parallelogram because
the diagonals bisect one another in M.
∠QRS ≠ 90° (12.3) and thus PQRS
is not a rectangle.
—————————————
13.3 d(BC) = √((xC − xB)2 + (yC − yB)2)
—————————————
= √((3 − (−6))2 + (−1 − 1)2 )
———— ——
= √81 + 4 = √85
—————————————
13.4 d(AD) = √((xD − xA)2 + (yD − yA)2)
—————————————
= √((7 − (−2))2 + (2 − 42 )
———— ——
= √81 + 4 = √85
d(AD) = d(BC) en dus is / and therefore AD = BC
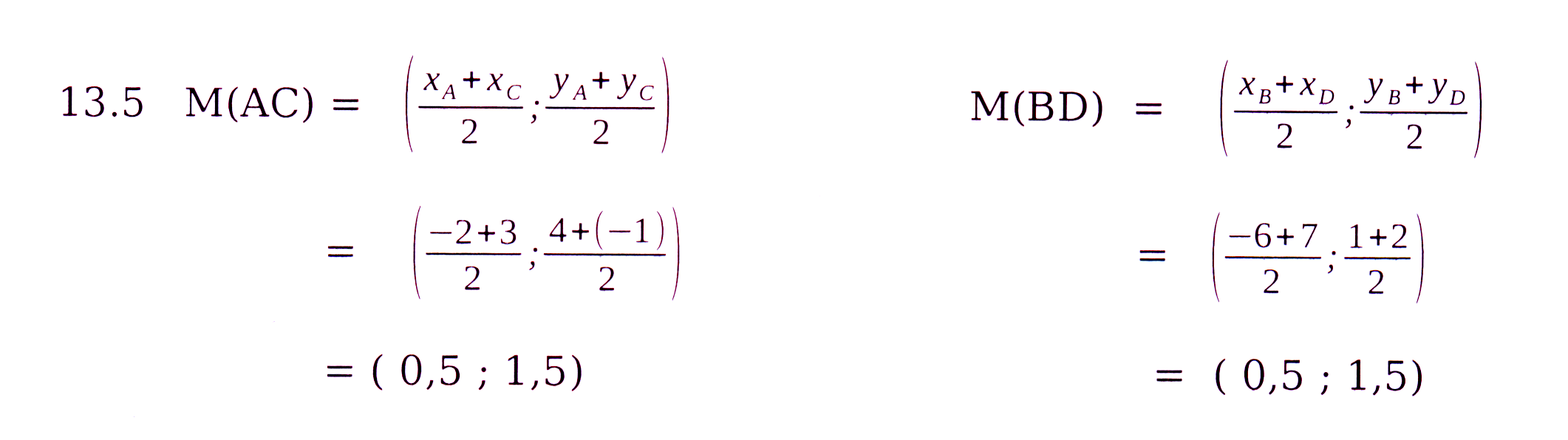
AC en BD het dieselfde middelpunt en dus halveer hulle mekaar. /
AC and BD have the same mipoint and therefore they bisect one another.
Vr. / Qu. 13.5
13.6 Een paar ooreenstemmend sye, AC en BD, is eweeydig aan mekaar (13.1 en 13.2) en is ewe lank (13.3 en 13.4)
Die hoeklyne, AC en BD, halveer mekaar in M (13.5)
One pair of opposite sides, AC and BD, are parallel (13.1 and 13.2) equal (13.3 and 13.4)
The diagonals, AC and BD, bisect each other in M (13.5)
14. As PS || QR dan is m(PS) = m(QR) / If PS || QR then m(PS) = m(QR)
yS − yP yR − yQ a − 2 2 − (−1)
─────── = ─────── : ─────── = ───────
xS − xP xR − xQ 2 − (−2) 4 − 1
a − 2 3
─────── = ─────── = 1
4 3
a − 2 = 4
a = 6
15.1 Bepaal die lengte van elke sy. / Determine the length of each side.
————————————— ————————————— —————————————
d(KL) = √((xL − xK)2 + (yL − yK)2) d(KM) = √((xM − xK)2 + (yM − yK)2) d(LM) = √((xM − xL)2 + (yM − yL)2)
————————————— ————————————— —————————————
= √((2 − (−2))2 + (6 − 3)2 ) = √((5 − (−2))2 + (2 − 3)2 ) = √((5 − 22 + (2 − 6)2 )
———— —— ———— —— ———— ——
= √16 + 9 = √25 = 5 = √49 + 1 = √50 = √9 + 16 = √25 = 5
d(KL) = d(LM) = 5 en dus / and therefore KL = LM.
∴ ∠LKM = ∠LMK en dus moet / and therefore ∠KLM = 90°
yL − yK 6 − 3
m(KL) = ─────── = ───────
xL − xK 2 − (−2)
3
= ───
4
3 4
m(KL) = m(LM) = ── × − ── = −1
4 3
∴ KL ⊥ LM
KL = LM en / and KL ⊥ LM
ΔKLM is 'n gelykbenige, reghoekige driehoek.
Vr. / Qu. 15.1
m(KL) = ─────── = ───────
xL − xK 2 − (−2)
3
= ───
4
3 4
m(KL) = m(LM) = ── × − ── = −1
4 3
∴ KL ⊥ LM
KL = LM en / and KL ⊥ LM
ΔKLM is 'n gelykbenige, reghoekige driehoek.
yM − yL 2 − 6
m(LM) = ─────── = ───────
xM − xL 5 − 2
−4 4
= ─── = − ──
3 3
ΔKLM is an isosceles, right-angled triangle.
m(LM) = ─────── = ───────
xM − xL 5 − 2
−4 4
= ─── = − ──
3 3
ΔKLM is an isosceles, right-angled triangle.
15.2 Oppervlakte / Area ΔKLM = ½bh = ½ × KL × LM
= ½ × KL × LM = ½ × 5 × 5 eenhede2 / units2
= 12,5 eenhede2 / units2
16.2 As PQRS 'n parallelogram is, is T ook
die middelpunt van QS. /
If PQRS is a parallelogram, T is also the
midpoint of QS.
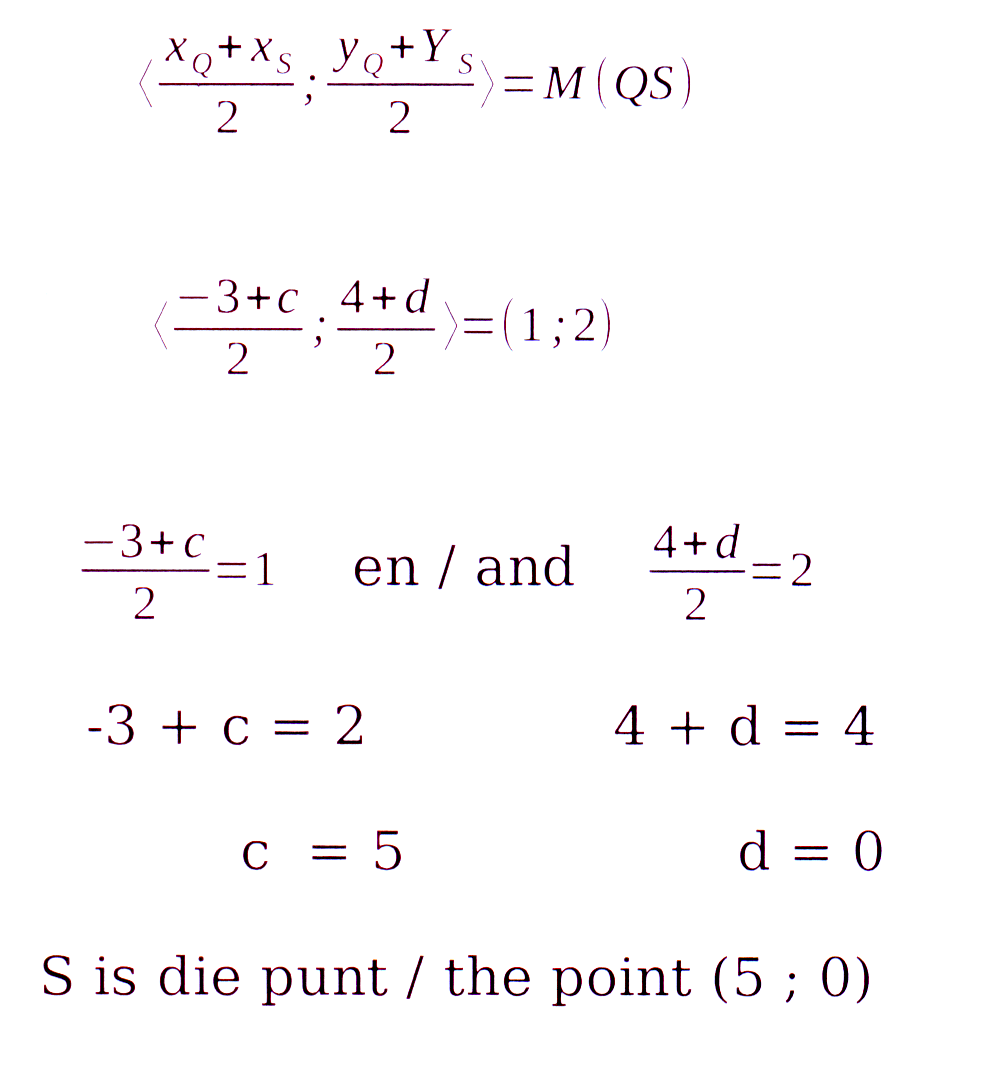
16.3 Hoeklyne PR en QS halveer mekaar in T
sodat PQRS 'n parallelogram is.
PQRS sal 'n reghoek wees as die
binnehoeke regte hoeke is.
As een hoek 'n reghoek is, is al die
ander binnehoeke ook regte hoeke.
Bewys dat ∠QPS = 90° deur aan te
toon dat m(PQ) X m(PS) = −1
Diagonals PR and QS bisect one another in T
and thus PQRS is a parallelogram.
PQRS will be a rectangle if the interior angles
are right angles.
If one angle is a right angle, the other angles will
also be right angles.
Prove that ∠QPS = 90° by showing that
m(PQ) X m(PS) = −1
yQ − yP yS − yP
m(PQ) × m(PS) = ─────── × ───────
xQ − xP xS − xP
4 − 6 0 − 6
= ─────── × ───────
−3 − 3 5 − 3
−2 −6
= ─── × ───
−6 2
= −1
Vraag / Question 16.3
ABCD is 'n trapesium as twee sye ewewydig
is aan mekaar.
Toets dus of AB || CD of AD || BC.
AB || CD as m(AB = m(CD) en
AD || BC as m(AD) = m(BC)
yB − yA 16 − 1
m(AB) = ─────── = ───────
xB − xA 4 − (−2)
5
= ───
2
ABCD is a trapezium if two sides are parallel.
Determine whether AB || CD or AD || BC.
AB || CD if m(AB = m(CD) and
AD || BC if m(AD) = m(BC)
5x − 2y − 20 = 0
2y = 5x − 20
5 5
y = ── x − 4 ∴ m(CD) = ──
2 2
∴ m(AB) = m(CD)
∴ AB || CD en dus is ABCD 'n trapesium. / and therefore ABCD is a trapezium.
Vraag / Question 17
∴ AB || CD en dus is ABCD 'n trapesium. / and therefore ABCD is a trapezium.
PQ en QR is twee aanliggende sye van 'n reghoek
as PQ ⊥ QR.
PQ ⊥ QR as m(PQ) × m(QR) = − 1.
Bepaal dus m(PQ) en m(QR) en beken die produk.
yQ − yP −2 − 13
m(PQ) = ─────── = ───────
xQ − xP 2 − (−4)
−5
= ───
2
as PQ ⊥ QR.
PQ ⊥ QR as m(PQ) × m(QR) = − 1.
Bepaal dus m(PQ) en m(QR) en beken die produk.
yQ − yP −2 − 13
m(PQ) = ─────── = ───────
xQ − xP 2 − (−4)
−5
= ───
2
PQ and QR are two adjacent sides of a rectangle
if PQ ⊥ QR.
PQ ⊥ QR if m(PQ) × m(QR) = − 1.
Thus, determine m(PQ) and m(QR) and calculate
the product.
2x − 5y − 5 = 0
5y = 2x − 5
2 2
y = ── x − 1 ∴ m(QR) = ──
5 5
if PQ ⊥ QR.
PQ ⊥ QR if m(PQ) × m(QR) = − 1.
Thus, determine m(PQ) and m(QR) and calculate
the product.
2x − 5y − 5 = 0
5y = 2x − 5
2 2
y = ── x − 1 ∴ m(QR) = ──
5 5
5 2
∴ m(PQ) × m(QR) = − ── × ── = − 1 ∴ PQ is loodreg op QR. / PQ is perpendicular to QR.
2 5
∴ PQ en QR kan die aanliggende sye van 'n reghoek wees. / PQ and QR can be adjacent sides of a rectangle.
Vraag / Question 18
∴ m(PQ) × m(QR) = − ── × ── = − 1 ∴ PQ is loodreg op QR. / PQ is perpendicular to QR.
2 5
∴ PQ en QR kan die aanliggende sye van 'n reghoek wees. / PQ and QR can be adjacent sides of a rectangle.