WISKUNDE
GRAAD 10
NOG OEFENINGE
Driehoeke en ewewydige lyne.
GRAAD 10
NOG OEFENINGE
Driehoeke en ewewydige lyne.
MATHEMATICS
GRADE 10
MORE EXERCISES
Triangles and parallel lines.
GRADE 10
MORE EXERCISES
Triangles and parallel lines.
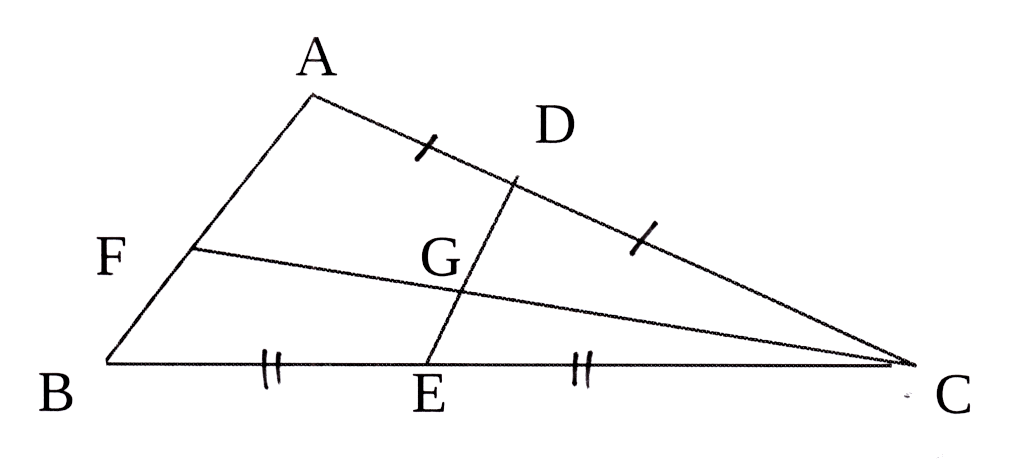
In meegaande skets is AD = DC en DE
halveer BC.
Gebruik die figuur en bewys, met redes, dat
FG = GC
In the accompanying diagram AD = DC and
DE bisects BC.
Use the diagram to prove, giving reasons, that
FG = GC
halveer BC.
Gebruik die figuur en bewys, met redes, dat
FG = GC
In the accompanying diagram AD = DC and
DE bisects BC.
Use the diagram to prove, giving reasons, that
FG = GC
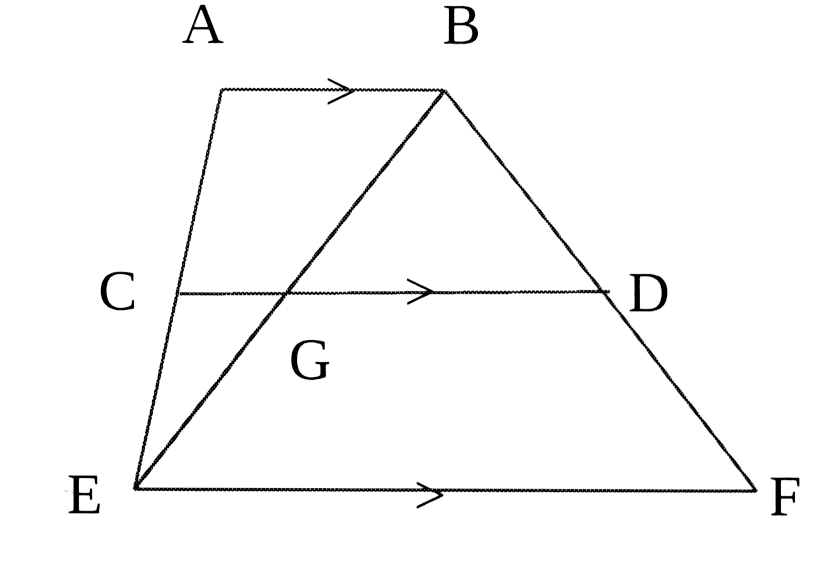
In meegaande skets is AB || CD || EF
en C is die middelpunt van AE.
Bewys, met redes, dat
2.1 BG = EG
2.2 BD = DF
2.3 CD = ½(AB + EF)
In the accompanying diagram AB || CD || EF
and C is the midpoint of AE.
Prove, giving reasons, that
2.1 BG = EG
2.2 BD = DF
2.3 CD = ½(AB + EF)
en C is die middelpunt van AE.
Bewys, met redes, dat
2.1 BG = EG
2.2 BD = DF
2.3 CD = ½(AB + EF)
In the accompanying diagram AB || CD || EF
and C is the midpoint of AE.
Prove, giving reasons, that
2.1 BG = EG
2.2 BD = DF
2.3 CD = ½(AB + EF)
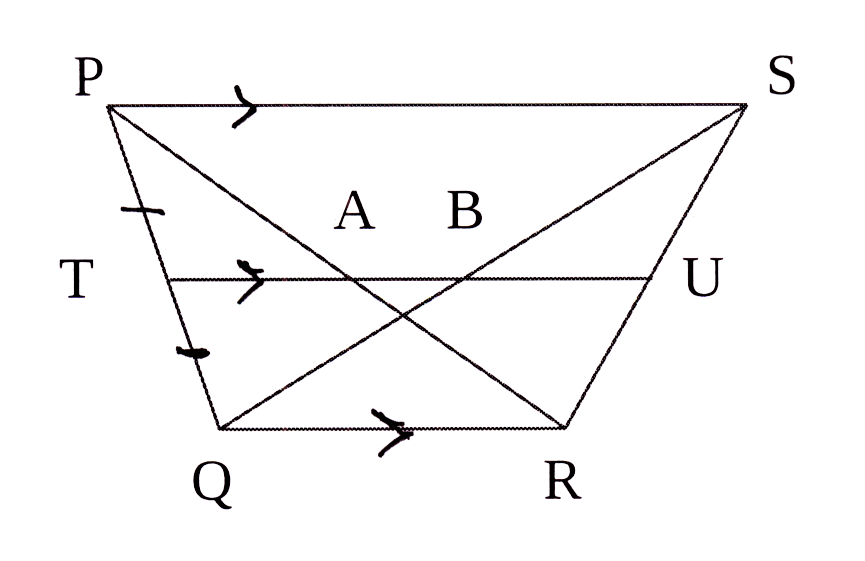
In meegaande skets is PS || TU || QR
en PT = TQ. Hoeklyne PR en QS sny TU in
A en B onderskeidelik.
Bewys, met redes, dat
3.1 TA = BU
3.2 AB = ½(PS − QR)
In the accompanying diagram PS || TU || QR
and PT = TQ. Diagonals PR and QS
intersect TU in A and B respectively.
Prove, giving reasons, that
3.1 TA = BU
3.2 AB = ½(PS − QR)
en PT = TQ. Hoeklyne PR en QS sny TU in
A en B onderskeidelik.
Bewys, met redes, dat
3.1 TA = BU
3.2 AB = ½(PS − QR)
In the accompanying diagram PS || TU || QR
and PT = TQ. Diagonals PR and QS
intersect TU in A and B respectively.
Prove, giving reasons, that
3.1 TA = BU
3.2 AB = ½(PS − QR)
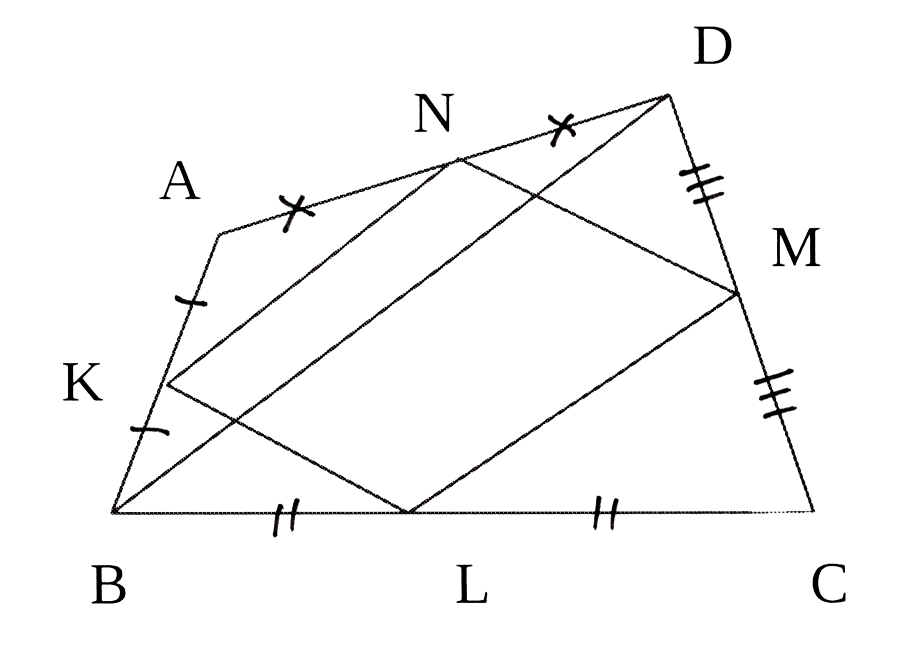
In meegaande skets is K, L, M en N die
middelpunte van AB, BC, CD en DA
onderskeidelik. BD is 'n hoeklyn.
Bewys, met redes, dat
4.1 KN || LM
4.2 KLMN is 'n parallelogram.
4.3 KL + LM + MN + NK = AC + BD
In the accompanying diagram K, L, M and N
are the midpoints of AB, BC, CD and DA
respectively. BD is a diagonal.
Prove, giving reasons, that
4.1 KN || LM
4.2 KLMN is a parallelogram.
4.3 KL + LM + MN + NK = AC + BD
middelpunte van AB, BC, CD en DA
onderskeidelik. BD is 'n hoeklyn.
Bewys, met redes, dat
4.1 KN || LM
4.2 KLMN is 'n parallelogram.
4.3 KL + LM + MN + NK = AC + BD
In the accompanying diagram K, L, M and N
are the midpoints of AB, BC, CD and DA
respectively. BD is a diagonal.
Prove, giving reasons, that
4.1 KN || LM
4.2 KLMN is a parallelogram.
4.3 KL + LM + MN + NK = AC + BD
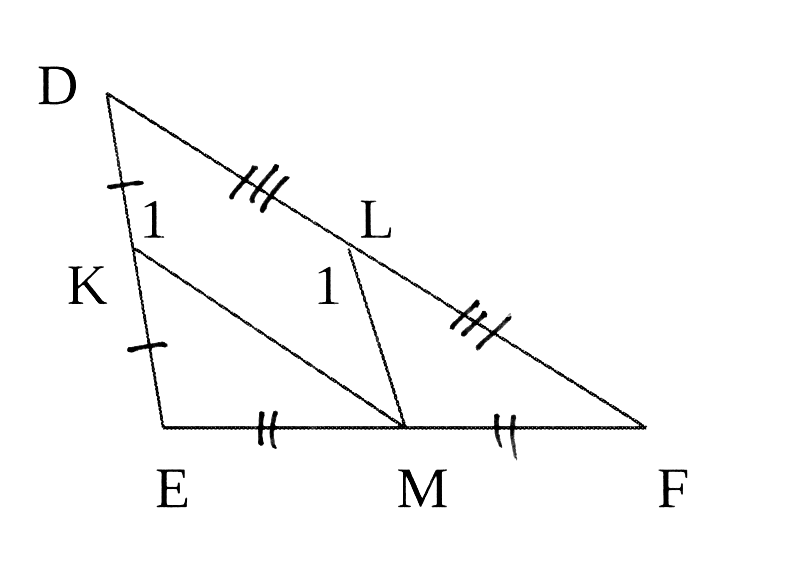
In meegaande skets is K, L en M die
middelpunte van DE, DF en EF
onderskeidelik. KM en LM is verbind.
Bewys, met redes, dat ∠K1 = ∠L1
In the accompanying diagram K, L and M
are the midpoints of DE, DF and EF
respectively. Lines KM and LM are drawn.
Prove, giving reasons, that ∠K1 = ∠L1
middelpunte van DE, DF en EF
onderskeidelik. KM en LM is verbind.
Bewys, met redes, dat ∠K1 = ∠L1
In the accompanying diagram K, L and M
are the midpoints of DE, DF and EF
respectively. Lines KM and LM are drawn.
Prove, giving reasons, that ∠K1 = ∠L1
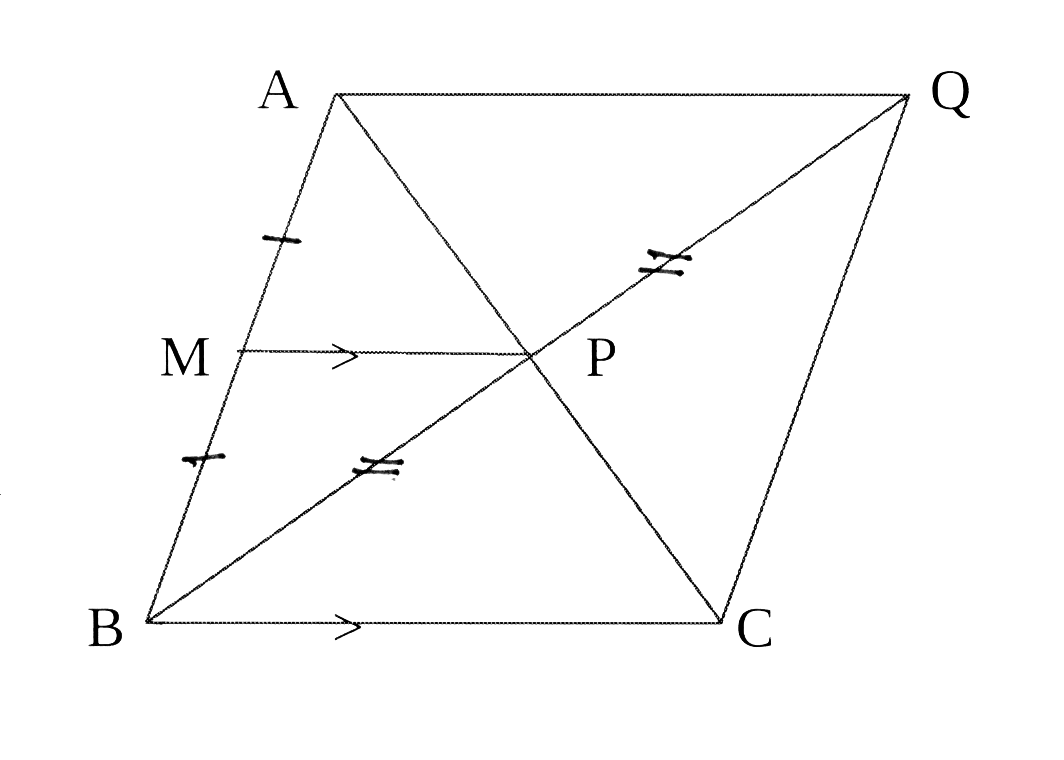
In meegaande skets is AM = MB en
MP || BC. BP word verleng na Q sodat
BP = PQ. Q word verbind met A en C.
Bewys, met redes, dat ABCQ 'n
parallelogram is.
In the accompanying diagram AM = MB and
MP || BC. BP is produced to Q so that
BP = PQ. Q is joined to A and C.
Prove, giving reasons, that ABCQ is
a parallelogram.
MP || BC. BP word verleng na Q sodat
BP = PQ. Q word verbind met A en C.
Bewys, met redes, dat ABCQ 'n
parallelogram is.
In the accompanying diagram AM = MB and
MP || BC. BP is produced to Q so that
BP = PQ. Q is joined to A and C.
Prove, giving reasons, that ABCQ is
a parallelogram.
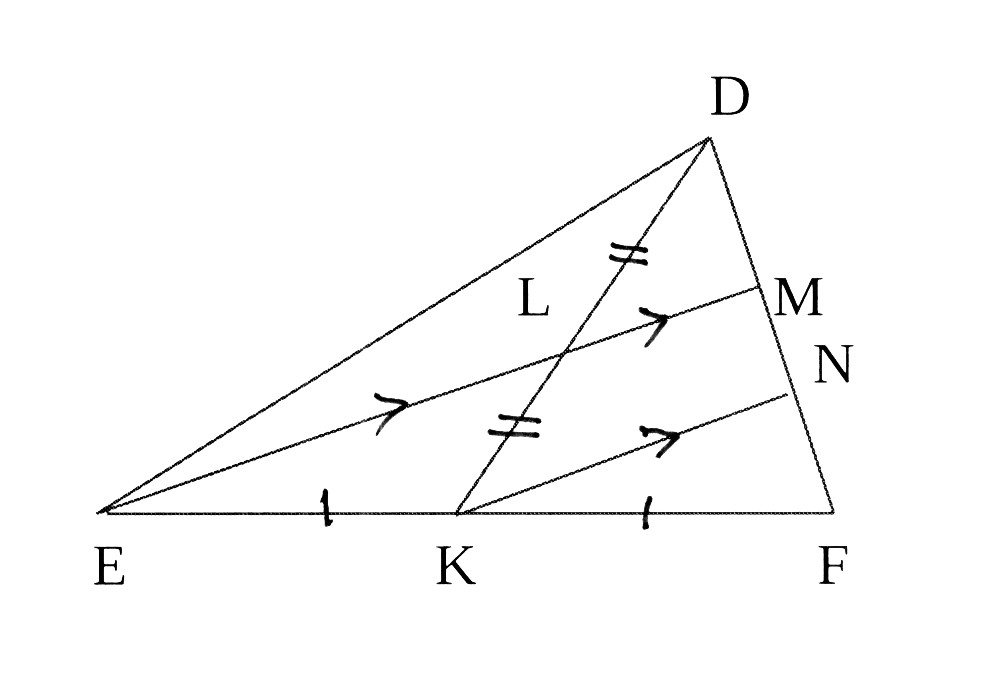
In Δ DEF is K die middelpunt van EF,
L die middelpunt van DK en EM || KN.
Bewys, met redes, dat DF = 3 DM.
In Δ DEF K is the midpoint of EF,
L is the midpoint of DK and EM || KN.
Prove, giving reasons, that DF = 3 DM.
L die middelpunt van DK en EM || KN.
Bewys, met redes, dat DF = 3 DM.
In Δ DEF K is the midpoint of EF,
L is the midpoint of DK and EM || KN.
Prove, giving reasons, that DF = 3 DM.