WISKUNDE
GRAAD 10
NOG OEFENINGE
Pythagoras se stelling.
GRAAD 10
NOG OEFENINGE
Pythagoras se stelling.
MATHEMATICS
GRADE 10
MORE EXERCISES
Theorem of Pythagoras.
GRADE 10
MORE EXERCISES
Theorem of Pythagoras.
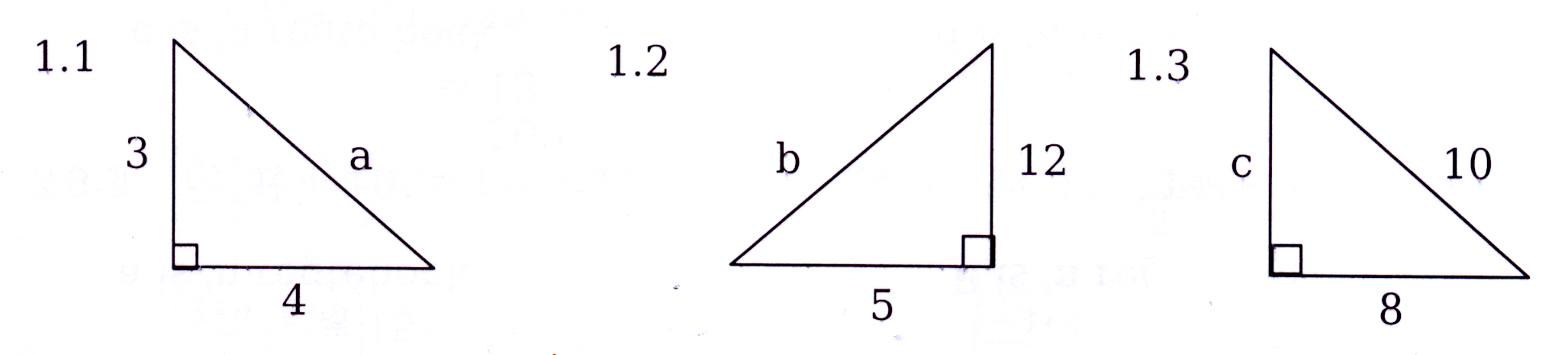
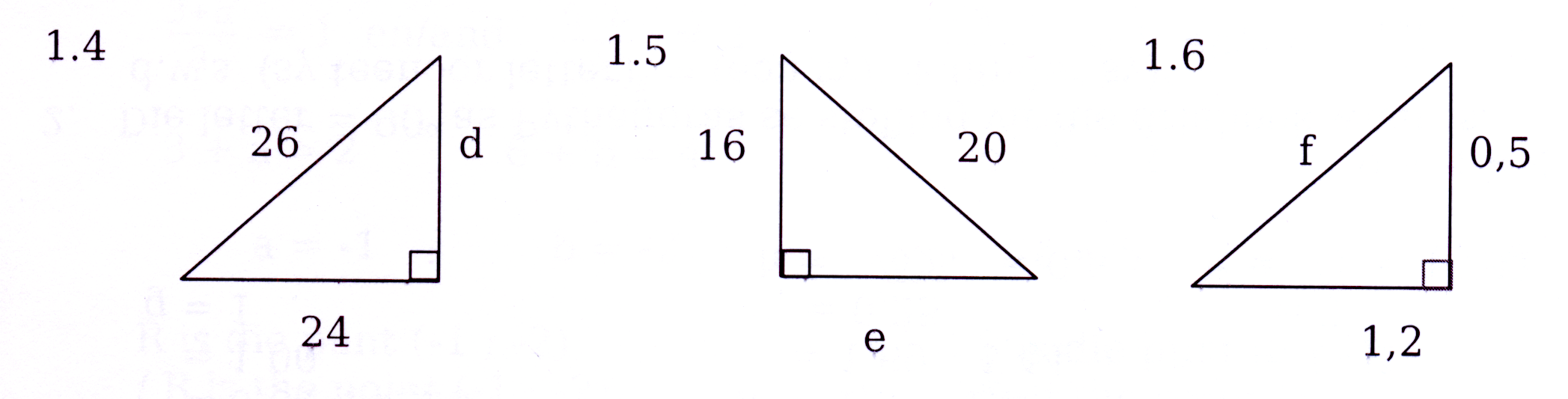
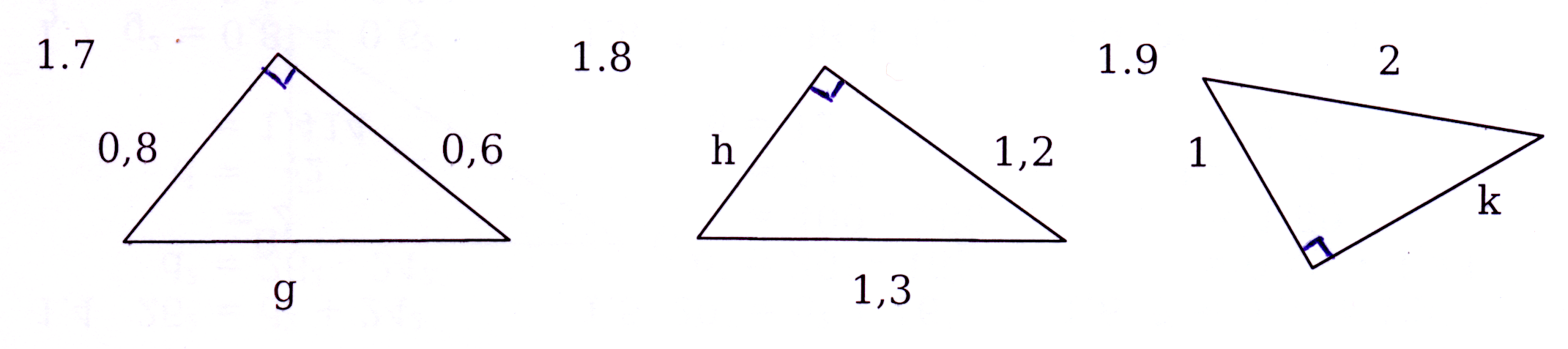
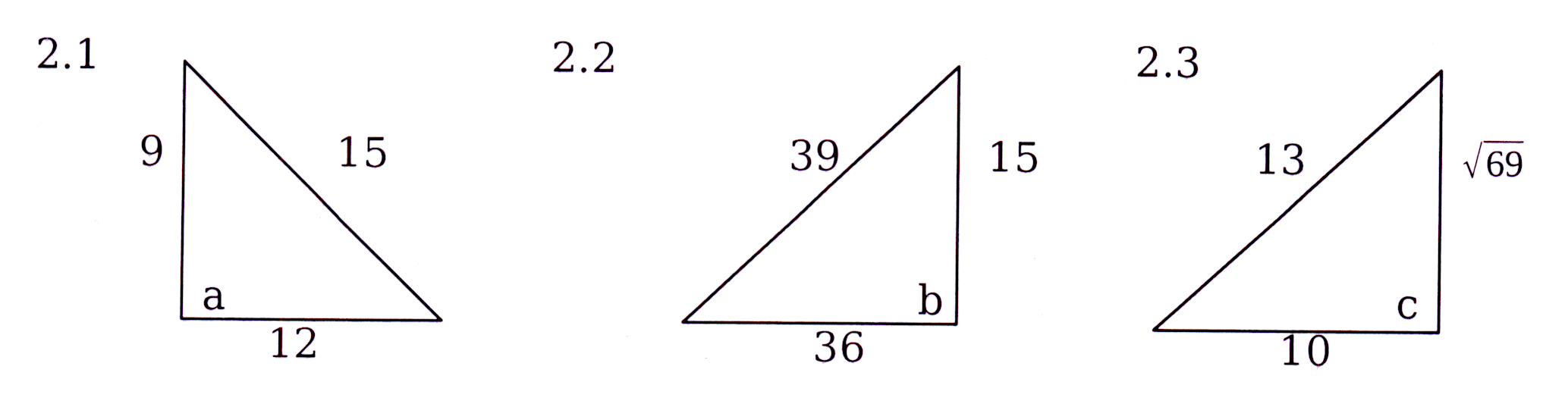
Bereken die waarde van elke letter in die figure hieronder.
Calculate the value of each letter in every figure below :
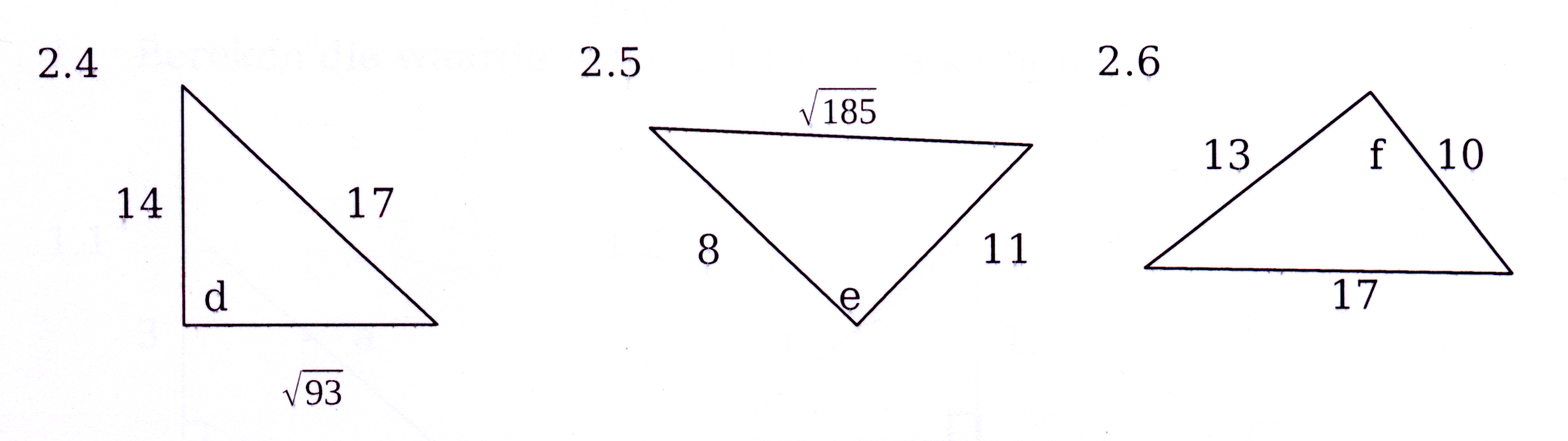
Bepaal of elke letter 'n regte hoek vereenwoordig.
Detemine if each letter represents a ight angle.
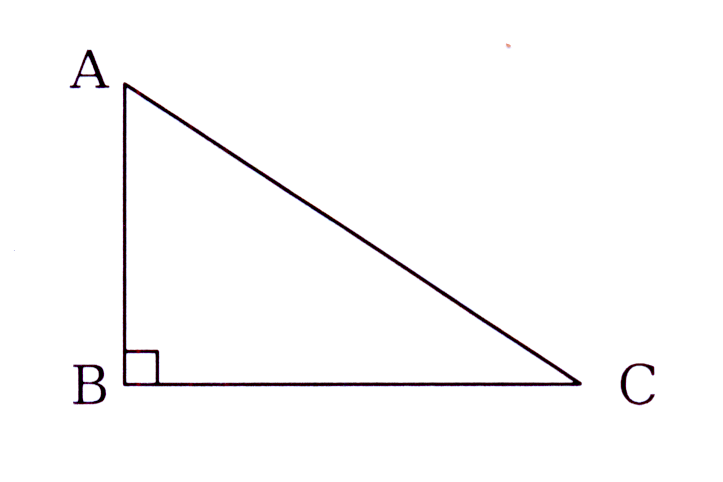
Die figuur toon 'n 4 m lange leer AC wat teen 'n hoë muur geplaas word.
Die voet van die leer, C, word 0,5 m vanaf die muur geplaas.
Bereken hoe hoog die leer teen die muur sal reik.
The figure shows a ladder, AC, 4 m length that is placed against a high wall.
The ladder is placed 0,5 m from the wall.
Calculate the height that the ladder will reach.
Antwoord / Answer 3.
.
Die voet van die leer, C, word 0,5 m vanaf die muur geplaas.
Bereken hoe hoog die leer teen die muur sal reik.
The figure shows a ladder, AC, 4 m length that is placed against a high wall.
The ladder is placed 0,5 m from the wall.
Calculate the height that the ladder will reach.
.
Die figuur toon 'n paal, PQ, 5 m lank, wat m.b.v. 'n ankertou, PR, gestut word.
Die tou word by punt R, 4 m vanaf die voet van die paal, vasgemaak.
Hoe lank is die ankertou?.
The figure shows a pole, PQ, 5 m tall, that is supported by a rope, PR.
The rope is fastened at point R, 4 m from the foot of the pole.
Calculate the length of the rope.
Antwoord / Answer 4.
.
Die tou word by punt R, 4 m vanaf die voet van die paal, vasgemaak.
Hoe lank is die ankertou?.
The figure shows a pole, PQ, 5 m tall, that is supported by a rope, PR.
The rope is fastened at point R, 4 m from the foot of the pole.
Calculate the length of the rope.
.
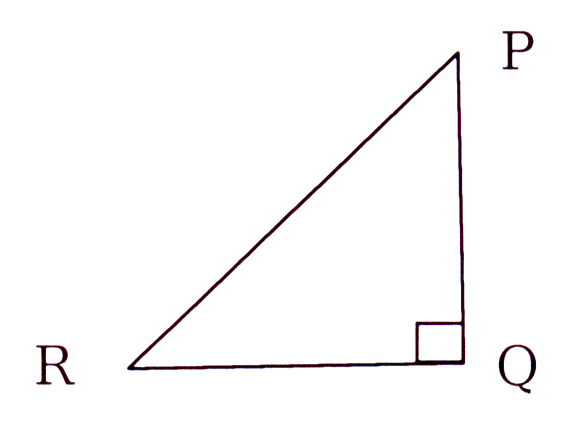
'n Vliegtuig is by punt A. Dit vlieg 500 km reg noord en daarna
500 km reg oos tot by punt C. Bereken die afstand van die vliegtuig
vanaf punt A.
The figure shows a pole, PQ, 5 m tall, that is supported by a rope, PR.
The rope is fastened at point R, 4 m from the foot of the pole.
Calculate the length of the rope.
Antwoord / Answer 5.
.
500 km reg oos tot by punt C. Bereken die afstand van die vliegtuig
vanaf punt A.
The figure shows a pole, PQ, 5 m tall, that is supported by a rope, PR.
The rope is fastened at point R, 4 m from the foot of the pole.
Calculate the length of the rope.
.
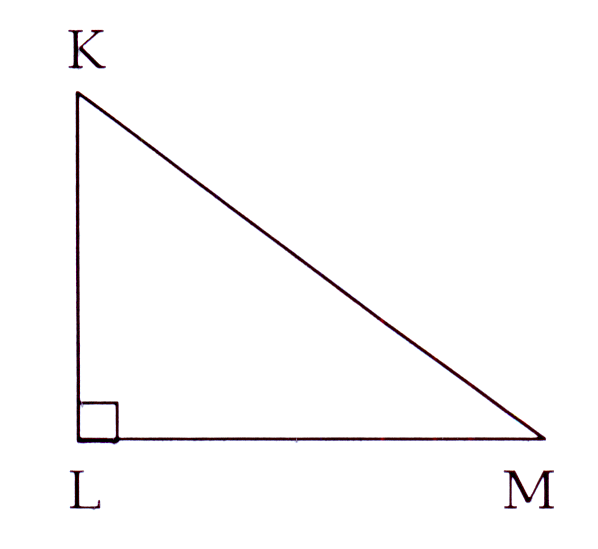
'n Boot is by punt M, 300 m vanaf 'n vertikale krans, KL. Die afstand vanaf die
boot na die bopunt van die krans, K, is 500 m. Hoe hoog is die krans?
A boat is at point M, 300 m from a vertical cliff, KL. The distance from
the boat to the top of the krans, K, is 500 m. How high is the krans?
Antwoord / Answer 6.
.
boot na die bopunt van die krans, K, is 500 m. Hoe hoog is die krans?
A boat is at point M, 300 m from a vertical cliff, KL. The distance from
the boat to the top of the krans, K, is 500 m. How high is the krans?
.

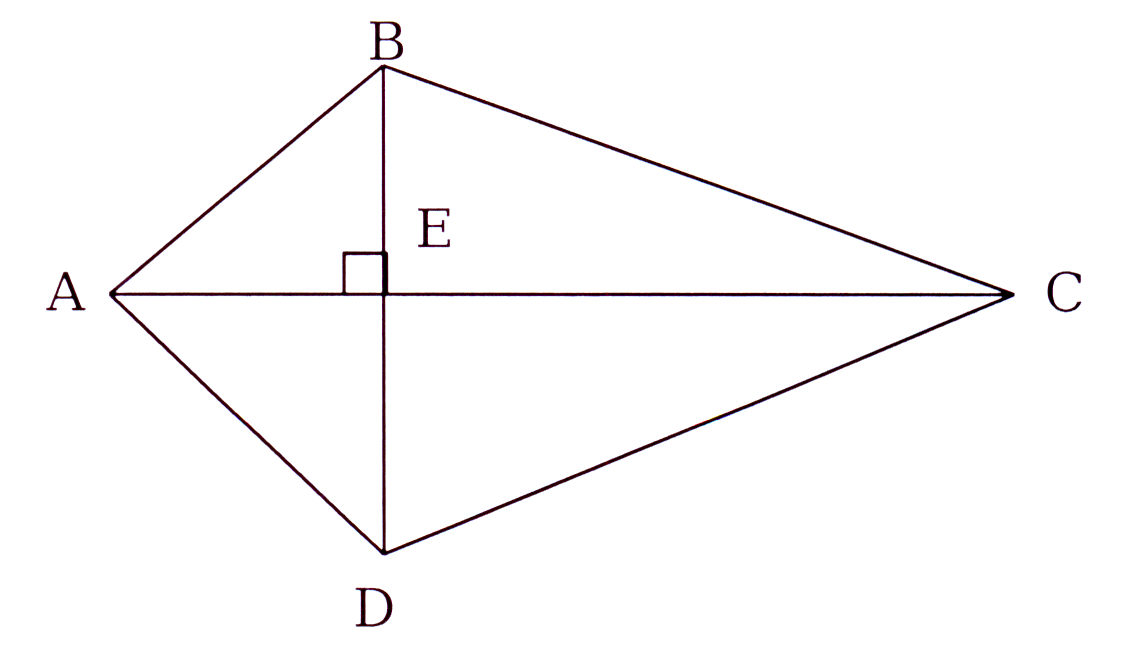
ABCD is 'n vliëer met AC = 12 cm, BD = 6 cm en AE = 4 cm.
Bepaal die lengte van die sye, korrek tot 1 desimale plek.
ABCD is a kite with AC = 12 cm, BD = 6 cm and AE = 4 cm.
Determine the length of each side, correct to 1 decimal.
Antwoord / Answer 7.
.
Bepaal die lengte van die sye, korrek tot 1 desimale plek.
ABCD is a kite with AC = 12 cm, BD = 6 cm and AE = 4 cm.
Determine the length of each side, correct to 1 decimal.
.
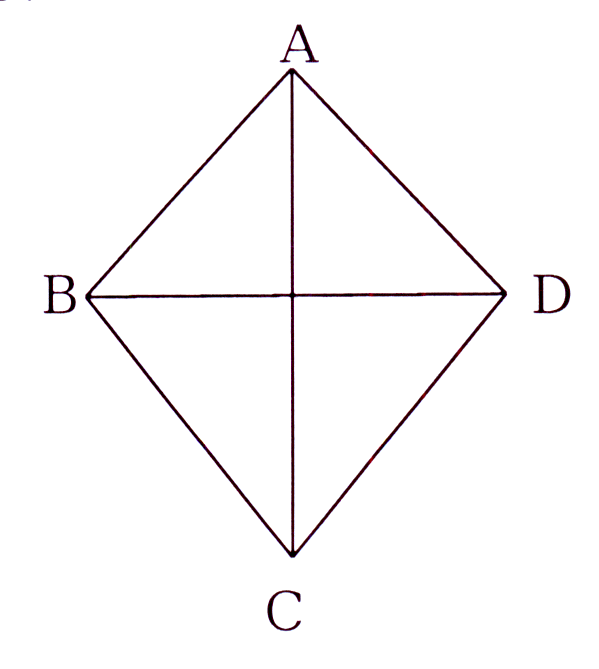
Elke sy van rhombus ABCD is 11 cm. Die hoeklyne sny in E.
Een diagonaal is 18 cm. Bereken die lengte van die ander hoeklyn,
korrek tot 2 desimale plekke.
The length of each side of rhombus ABCD is 11 cm. One diagonal is
is 18 cm. Determine the length of the other diagonal, correct
to 2 decimals.
Antwoord / Answer 8.
.
Een diagonaal is 18 cm. Bereken die lengte van die ander hoeklyn,
korrek tot 2 desimale plekke.
The length of each side of rhombus ABCD is 11 cm. One diagonal is
is 18 cm. Determine the length of the other diagonal, correct
to 2 decimals.
.
In ΔABC is AD ⊥ BC en AB = AC. BD = 3 cm, AB = 5 cm en
BC = 6 cm. Bepaal AD.
In ΔABC AD ⊥ BC and AB = AC. BD = 3 cm, AB = 5 cm and
BC = 6 cm. Determine the length of AD.
Antwoord / Answer 9.
.
BC = 6 cm. Bepaal AD.
In ΔABC AD ⊥ BC and AB = AC. BD = 3 cm, AB = 5 cm and
BC = 6 cm. Determine the length of AD.
.

A110Apyta
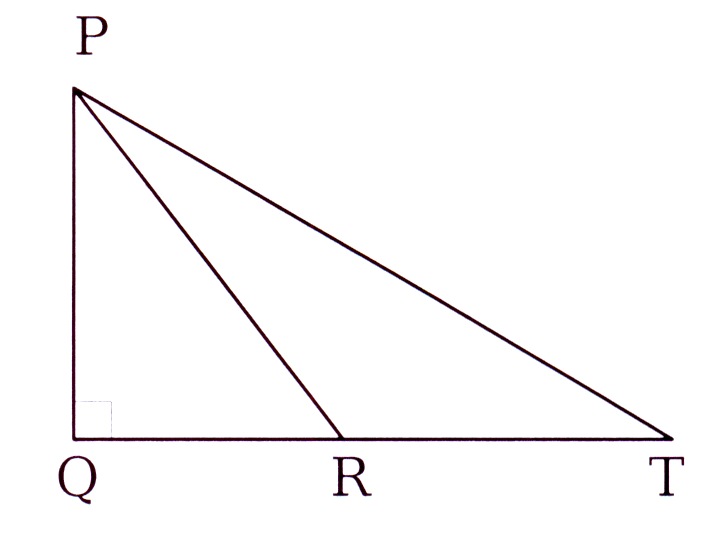
In ΔPQT is ∠PQT = 90°, PR = 17 mm, QR = 8 mm en RT = 4 mm.
Bepaal PT, korrek tot 3 desimale plekke.
In ΔPQT ∠PQT = 90°, PR = 17 mm, QR = 8 mm and RT = 4 mm.
Determine the length of PT, correct to 3 decimals.
Antwoord / Answer 10.
.
Bepaal PT, korrek tot 3 desimale plekke.
In ΔPQT ∠PQT = 90°, PR = 17 mm, QR = 8 mm and RT = 4 mm.
Determine the length of PT, correct to 3 decimals.
.
11.1 Toon aan dat 'n driehoek met sye m2 + n2, m2 − n2
en 2mn 'n reghoekige driehoek is.
Antwoord 11.1
11.2 'n Driehoek het sye 4n, 4n2 − 1 en 4n2 + 1. Is die
driehoek 'n reghoekige driehoek?
Antwoord 11.2
.
en 2mn 'n reghoekige driehoek is.
11.2 'n Driehoek het sye 4n, 4n2 − 1 en 4n2 + 1. Is die
driehoek 'n reghoekige driehoek?
.
11.1 Show that a triangle having sides of m2 + n2, m2 − n2
and 2mn is a right-angled triangle.
Answer 11.1
11.2 A triangle has sides with lengths 4n, 4n2 − 1 and 4n2 + 1. Is the
triangle a right-angled triangle?
Answer 11.2
.
and 2mn is a right-angled triangle.
11.2 A triangle has sides with lengths 4n, 4n2 − 1 and 4n2 + 1. Is the
triangle a right-angled triangle?
.
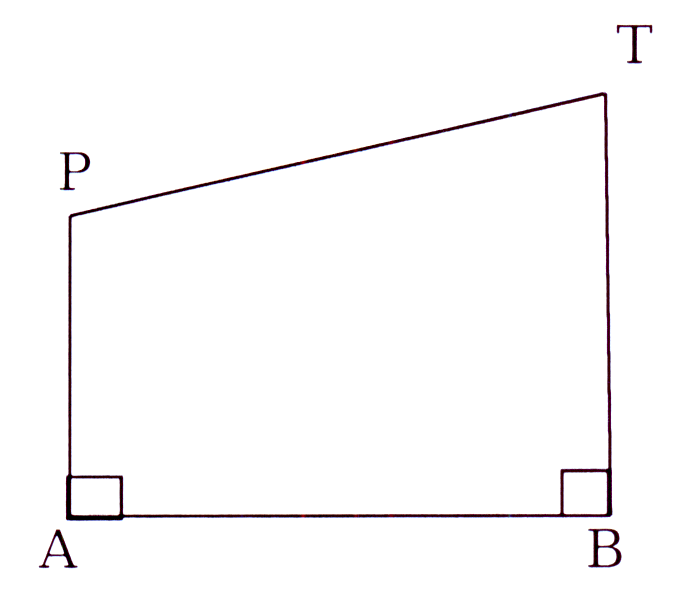
P en T is punte aan dieselfde kant van AB sodat
PA ⊥ AB en TB ⊥ AB. Verder is AB = 240 m, PA = 60 m
en TB = 120 m. Bepaal PT, korrek tot 2 desimale plekke.
P and T are points on the same side of AB so that
PA ⊥ AB and TB ⊥ AB. Furthermore Verder is AB = 240 m, PA = 60 m
en TB = 120 m. Bepaal PT, korrek tot 2 desimale plekke.
Antwoord / Answer 12.
.
PA ⊥ AB en TB ⊥ AB. Verder is AB = 240 m, PA = 60 m
en TB = 120 m. Bepaal PT, korrek tot 2 desimale plekke.
P and T are points on the same side of AB so that
PA ⊥ AB and TB ⊥ AB. Furthermore Verder is AB = 240 m, PA = 60 m
en TB = 120 m. Bepaal PT, korrek tot 2 desimale plekke.
.
'n Leer wat 5 m lank is word met sy voet 3 m vanaf 'n muur geplaas.
Hoeveel nader aan die muur moet die voet geplaas word sodat die
leer 'n punt 800 mm hoër te bereik?
Antwoord 13.
Hoeveel nader aan die muur moet die voet geplaas word sodat die
leer 'n punt 800 mm hoër te bereik?
A ladder, length 5 m, is placed against a wall with its foot 3 m from
the wall. How much closer to the wall must the foot be placed so that
the ladder will reach a point 800 mm higher?
Answer 13.
the wall. How much closer to the wall must the foot be placed so that
the ladder will reach a point 800 mm higher?
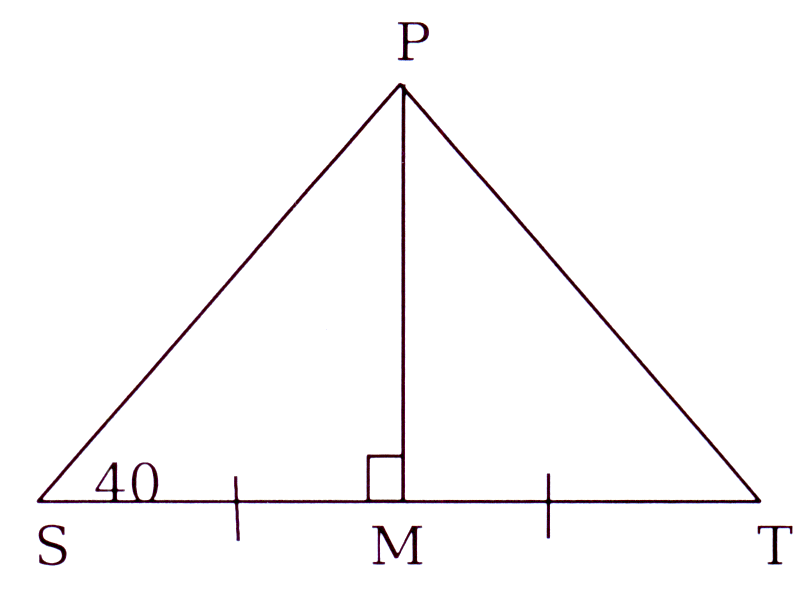
PST is 'n driehoek met ∠P = 90°. M is 'n punt op ST sodat PM = MT.
As ∠S = 40°, bewys dat SM = MT. As PS = 48 mm en PT = 64 mm,
bereken die lengte van PM.
PST is a triangle with ∠P = 90°. M is a point on ST so that PM = MT.
If ∠S = 40°, prove that SM = MT. If PS = 48 mm and PT = 64 mm,
calculate the length of PM.
Antwoord / Answer 14.
.
As ∠S = 40°, bewys dat SM = MT. As PS = 48 mm en PT = 64 mm,
bereken die lengte van PM.
PST is a triangle with ∠P = 90°. M is a point on ST so that PM = MT.
If ∠S = 40°, prove that SM = MT. If PS = 48 mm and PT = 64 mm,
calculate the length of PM.
.
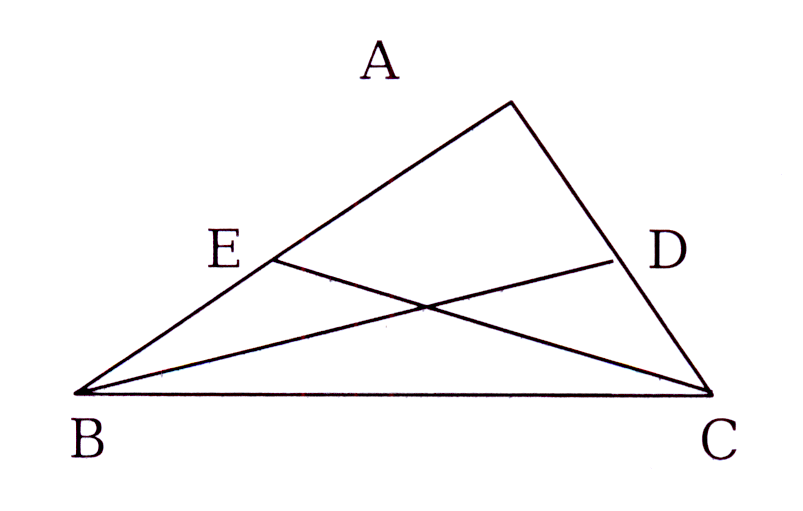
In driehoek ABC is ∠A 'n regte hoek. D is 'n punt op AC en
E 'n punt op AB. Bewya dat CE2 + BD2 = ED2 + BC2
In triangle ABC, ∠A is a right angle. D is a point on AC and
E a point on AB. Prove that CE2 + BD2 = ED2 + BC2
Antwoord / Answer 15.
.
E 'n punt op AB. Bewya dat CE2 + BD2 = ED2 + BC2
In triangle ABC, ∠A is a right angle. D is a point on AC and
E a point on AB. Prove that CE2 + BD2 = ED2 + BC2
.
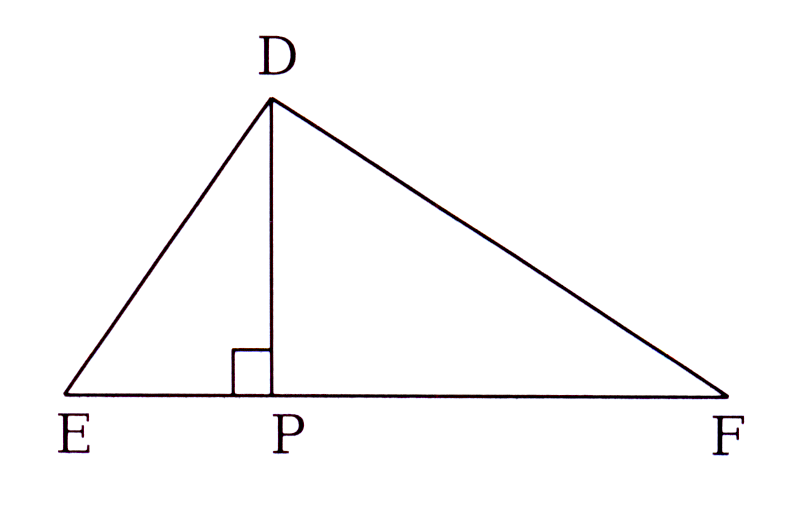
In driehoek ABC is P 'n punt op EF sodat DP ⊥ EF.
Bewys dat DE2 + PF2 = EP2 + DF2
In triangle DEF, P is a point on EF so that DP ⊥ EF.
Prove that DE2 + PF2 = EP2 + DF2
Antwoord / Answer 16.
.
Bewys dat DE2 + PF2 = EP2 + DF2
In triangle DEF, P is a point on EF so that DP ⊥ EF.
Prove that DE2 + PF2 = EP2 + DF2
.
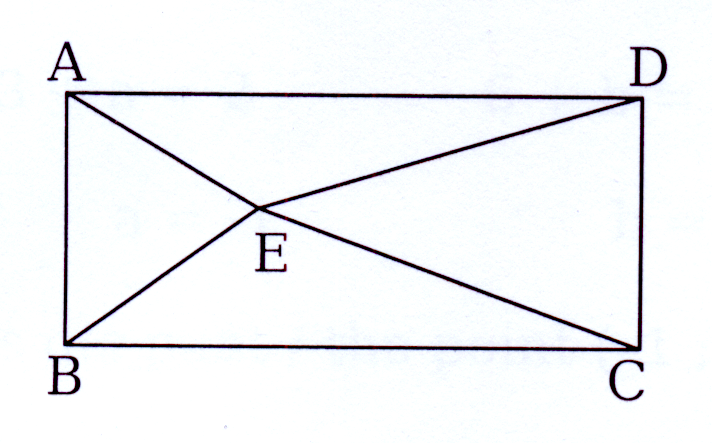
E is enige punt binne die reghoek ABCD.
Bewys dat EA2 + EC2 = EB2 + ED2
E is any point inside the rectangle ABCD.
Prove that EA2 + EC2 = EB2 + ED2
Antwoord / Answer 17.
.
Bewys dat EA2 + EC2 = EB2 + ED2
E is any point inside the rectangle ABCD.
Prove that EA2 + EC2 = EB2 + ED2
.