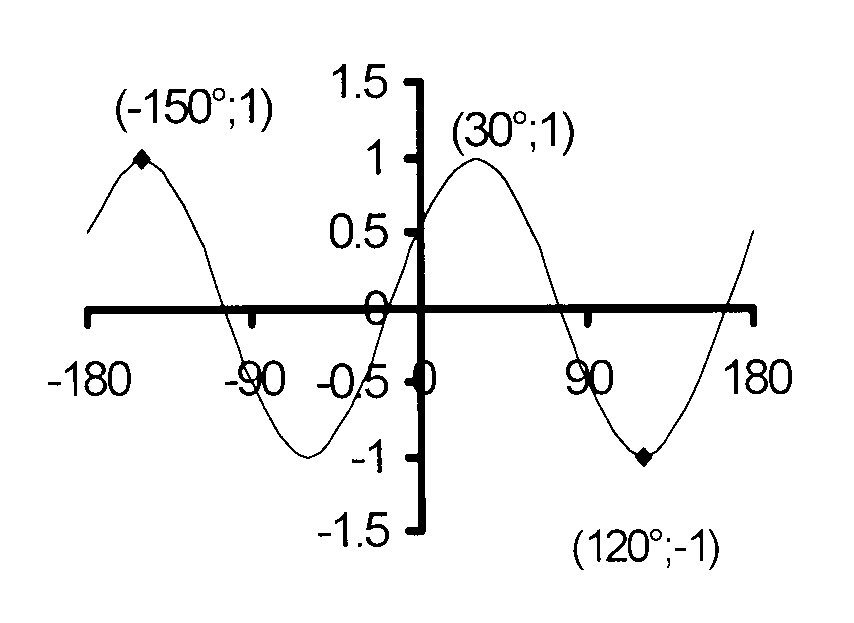Grade 11 Mathematics - More Exercises.
Graphs of sin x, cos x and tan x : answers.
1.1
y = 3 cos x − 2
1.2
y = 1 − sin x
Vertical translation : q = − 2 and the graph
Vertical translation : q = − 1 and the graph
oscillates about y = − 2
oscillates about y = − 1
amplitude = 3 and thus
amplitude = 1 and thus
maximum = − 2 + 3 = 1
maximum = 1 + 1 =
minimum = −2 − 3 = − 5
minimum = 1 − 1 = 0
There is no horizontal translation; p = 0
There is no horizontal translation; p = 0
Period = 360°
Period = 360°
The maxiimum is reached at 0°
The maxiimum is reached at −90°
The minimum is reached at −180° and
The minimum is reached at 90°
at 180°

1.3
y = cos (2x − 60°) = cos 2(x − 30°)
1.4
y = sin (x + 30°)
Vertical translation : q = 0 and the graph
Vertical translation : q = 0 and the graph
oscillates about y = 0; the X-axis
oscillates about y = 0 ; the X-axis
amplitude = 1 and thus maximum = 1
amplitude = 1 and thus maximum = 1
and minimum = − 1
and minimum = − 1
k = 2 and period = 180°
k = 1 and period = 360°
Horizontal translation; p = 30° to the right.
Horizontal translation; p = 30° to the left.
The maxiimum is reached at − 150° and
The maxiimum is reached at 120°
at 30°
The minimum is reached at −60° and
The minimum is reached at − 60°
at 120°
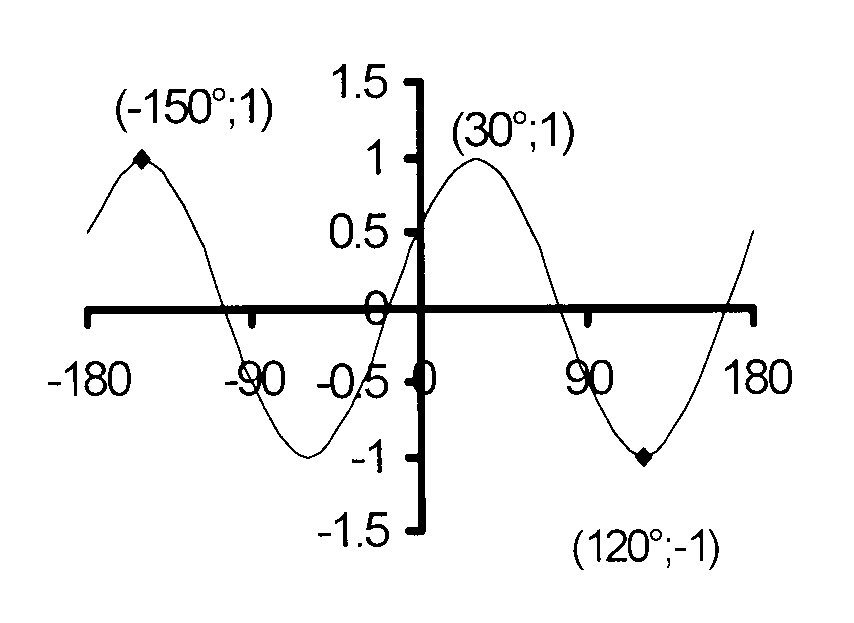

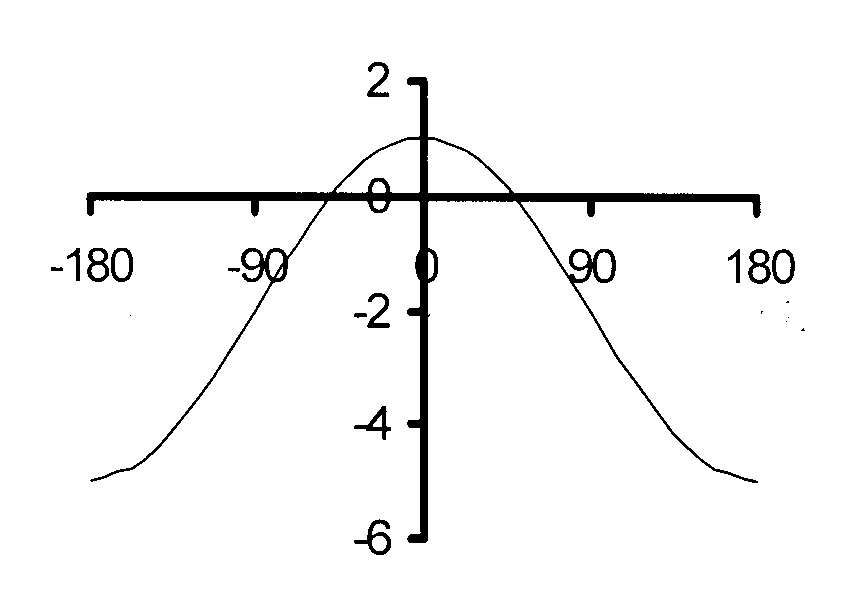
1.5
y = cos (x + 30°) −1
1.6
y = sin (x + 60°) + 1
Vertical translation : q = − 1 and the graph
Vertical translation : q = 1 and the graph
oscillates about y = − 1
oscillates about y = 1
amplitude = 1 and thus
amplitude = 1 and thus
maximum = 1 − 1 = 0
maximum = 1 + 1 = 2
and minimum = −1 − 1 = −2
and minimum = 1 − 1 = 0
k = 1 and period = 360°
k = 1 and period = 360°
Horizontal translation; p = 30° to the left.
Horizontal translation; p = 60° to the left.
The maximum is reached at − 30°
The maximum is reached at 30°
The minimum is reached at 150°
The minimum is reached at − 150°
2.1
y = a sin k(x + p)
2.2
y = a cos k(x + p)
The graph oscillates about y = 0; the X-axis
The graph oscillates about y = 0; the X-axis
and thus q = 0
and thus q = 0
360°
360°
period = 180° and k = ——— = 2
period = 120° and k = ——— = 3
180°
120°
Horizontal translation is 30° to the left; p = +30°.
Horizontal translation is 30° to the right; p = −30°
Equation: y = 1. sin 2x + 30°
Equation: y = 2. cos 3x − 30°
= sin 2(x + 15°)
= 2 cos 3(x − 10°)
2.3
y = a sin k(x + p)+ q
2.3
y = a cos k(x + p) + q
The graph oscillates about y = 0; the X-axis
The graph oscillates about y = 0; the X-axis
and thus q = 0
and thus q = 0
amplitude = 2 and thus a = 2
amplitude = 3 and the graph
is a cosine graph so that a = − 3
360°
360°
period = 120° and k = ——— = 3
period = 180° and k = ——— = 2
120°
180°
At A(20° ; 0): 3(20° + p) = 0°
At A(15° ; 0): 2(15° + p) = 90°
60° + 3p = 0°
30° + 2p = 90°
p = − 20°
p = 30°
Equation: y = 2. sin 3(x − 20°)
Equation: y = − 3. cos 2(x + 30°)
= 2 sin 3(x − 20°)
= − 3 cos 2(x + 30°)
2.5
y = a sin k(x + p)+ q
2.6
y = a cos k(x + p) + q
The graph oscillates about y = − 2
The graph oscillates about y = − 2
and thus q = − 2
and thus q = − 2
amplitude = 3 and thus a = 3
amplitude = 3 and thus a = 3
360°
period = 360° and k = 1
period = 180° and k = ——— = 2
180°
There is no horizontal translation and p = 0°
There is no horizontal translation and p = 0°
Equation: y = 3. sin (x + 0°) − 2
Equation: y = 3. cos 2(x + 0°) − 2
= 3 sin x − 2
= 3 cos 2x − 2
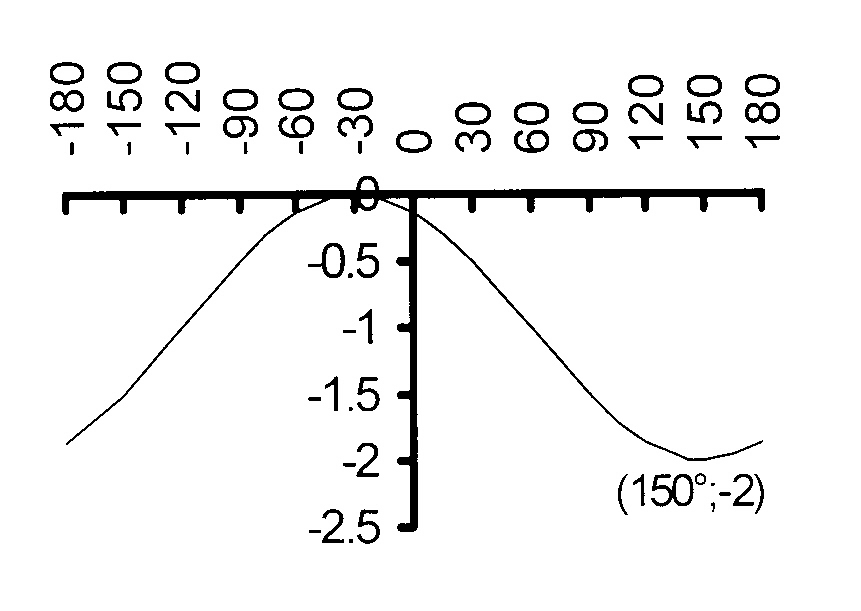
3.1
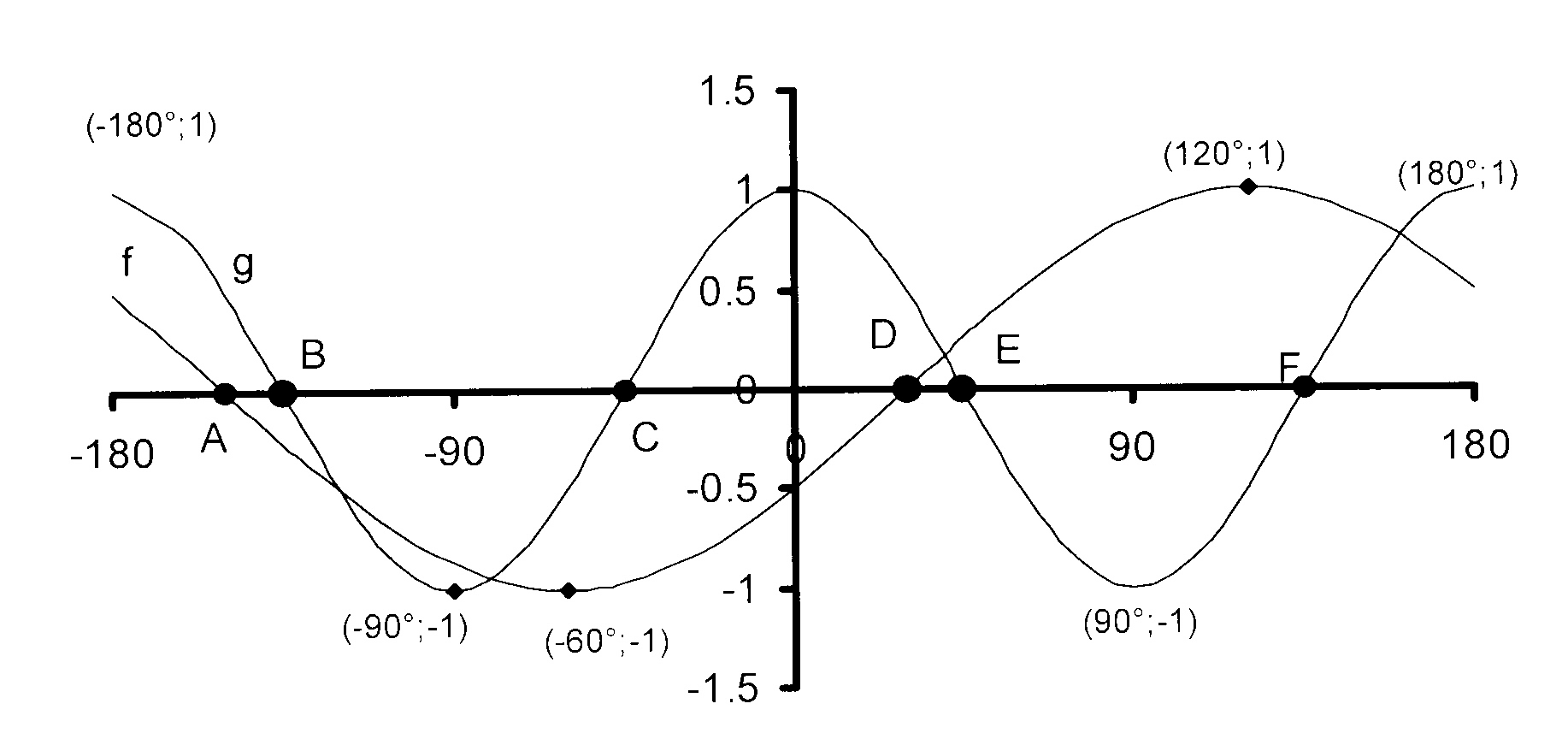
A(− 150°;0); B(− 135°;0);C(− 45°;0);
D(30°;0); E(45°;0); F(135°;0)
3.2
period = 360°
3.3
sin (x − 30°) = cos 2x
= sin (90° − 2x)
x − 30° = 90° − 2x + n.360°
OR
x − 30° = 180° − (90° − 2x) + n.360°
3x = 120° + n.360°
x − 30° = 180° − 90° + 2x + n.360°
x = 40° + n.120° ; n ∈ Z
− x = 120° + n.360°
x = − 120° − n.360°
Solution : x = − 120° −0.360°
; 40° − 1.120°
; 40° + 0.120°
; 40° + 0.120°
Solution : x = − 120° ; − 80° ; 40° ; 160°
4.1
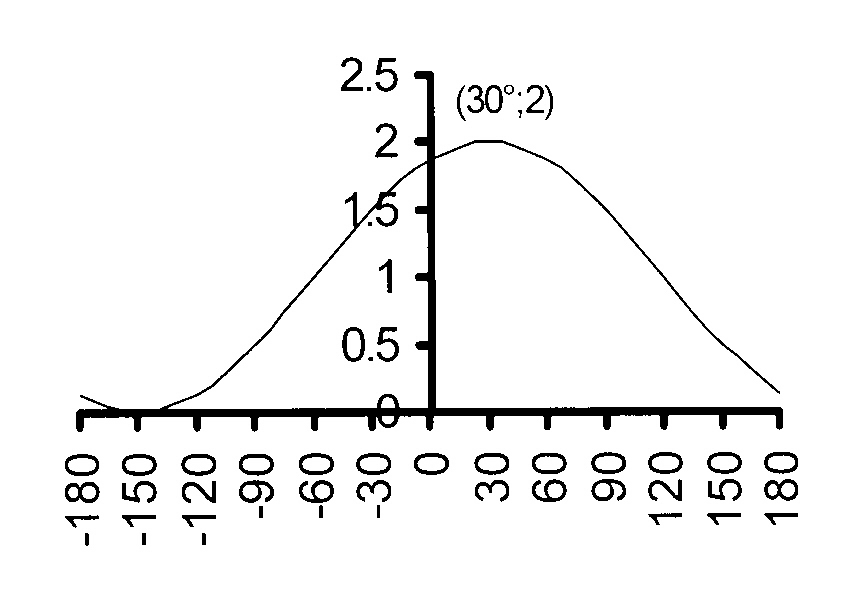
amplitude of cosine graph = 2 and thus a = 2; the cosine graph reaches 0 at 60° in stead of 90°
so that the graph is shifted 30° to the left and thus b = 30°
the sine graph oscillates about y = 1 so that c = 1 ; the period = 180° and thus d = 2.
4.2
f(x) = 2 cos (x + 30°)
f(0) = 2 cos (0 + 30°) = 2 cos 30° = √3
4.3.1
x = 45° and x = −135°
4.3.2
f and g intersect at(−90° ; 1) and at (13,5° ; 1,45);
hence solution: −90° ≤ x ≤ 13,5°
4.4
y = 2 cos x
5.1
amplitude of cosine graph = 1 and thus a = 1; the cosine graph reaches 1 at 30° in stead of 0°
so that the graph is shifted 30° to the right and thus b = −30°
the sine graph has a period = 360° and thus c = 1.
5.2.1
Range : − 0,5 ≤ y ≤ 1
5.2.2
30° < x ≤ 90°
5.2.3
−90° ≤ x ≤ −60° and x = 0°
5.3
cos (x − 30°) = sin x
= cos (90° − x)
∴ x − 30° = 90° − x + n360°
n ∈ Z
∴ 2x = 120° + n360°
∴ x = 60° + n360°
∴ x = 60°
If g(x) > f(x) then 60° < x ≤ 90°
6.1
amplitude = 2 and hence c = 2 and period = 360° and thus d = 1
6.2
amplitude = 1 and thus a = 1; f(60°) = 1 and thus graph is shifted 60° to the right so that b = − 60°
6.3
range: − 2 ≤ y ≤ 2
6.4
− 120° ≤ x ≤ − 30°
6.5
y = 2 sin (x − 30°)