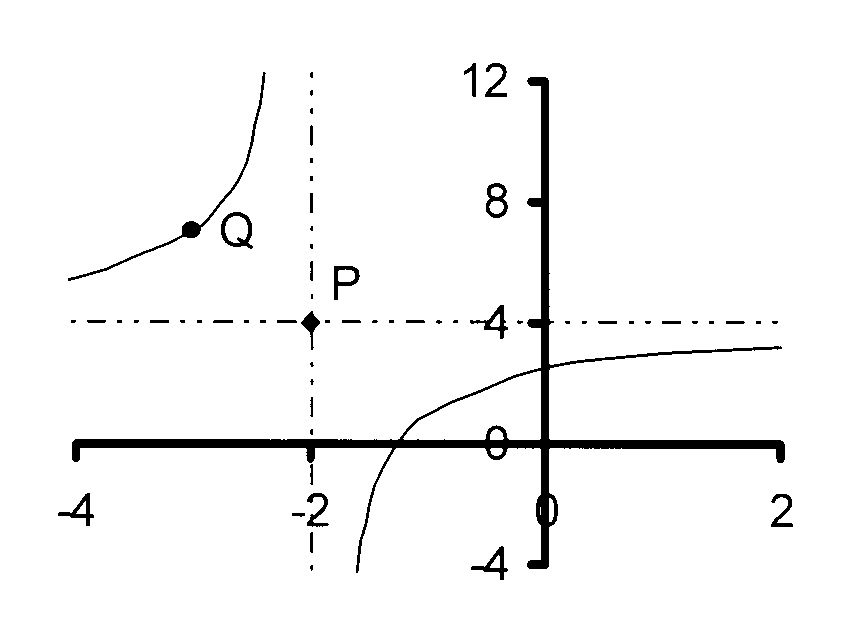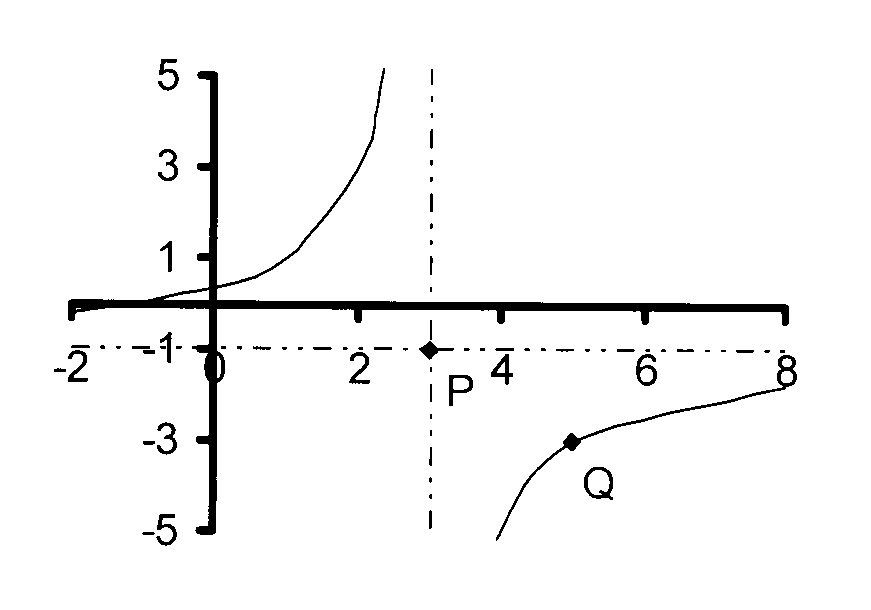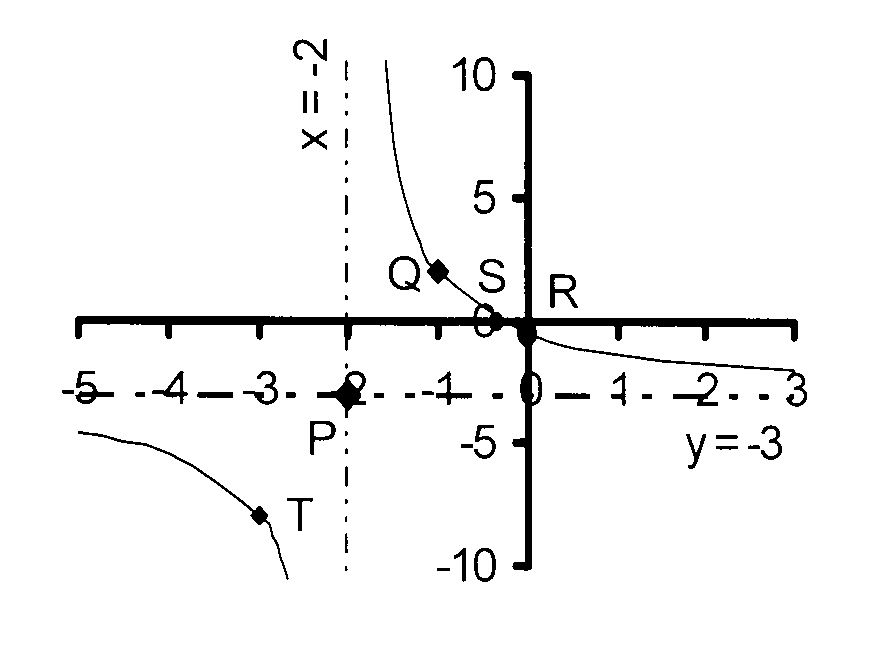Grade 11 Mathematics - More Exercises.
Graphs of the hyperbola.
1.
Sketch the graphs of the following functions:
2
3
5
1.1
y = ––––––– + 3
1.2
y = ———— – 4
1.3
y = ———— + 5
x + 1
x + 2
x - 3
–2
− 3
− 5
1.4
y = ––––––– + 3
1.5
y = ———— – 4
1.6
y = ———— – 2
x + 1
x − 2
x + 3
a
2.
The figures show the graphs of the functions with equation y = ——— + q. Use the information given
x + p
in the figure to detemine the values of a, p and q :
2.1
2.2

Horizontal asymptote: y = 3 and vertical symptote: x = - 1
A is the point (−2 ; 0) and B(0 ; 6)
B is the point (0 ; − 8)
2.3
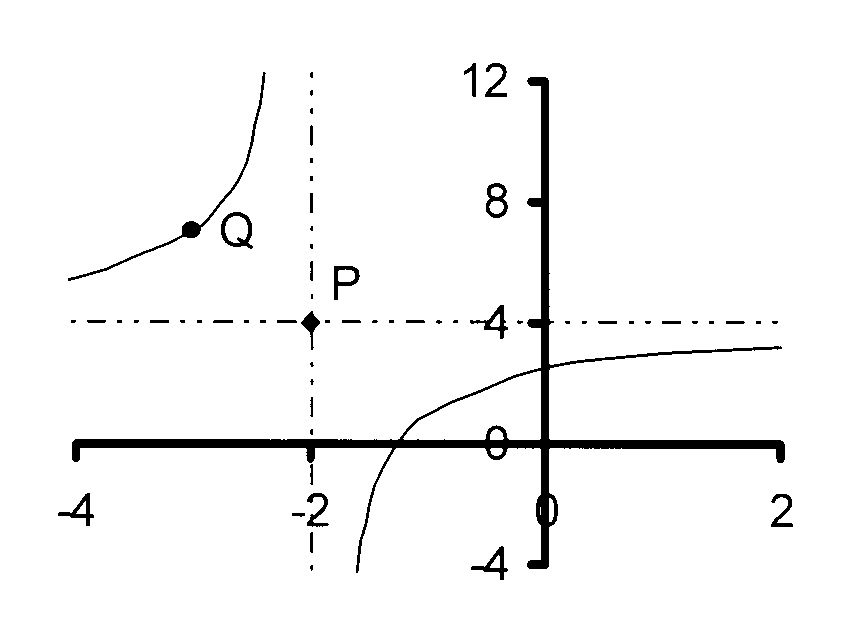
2.4
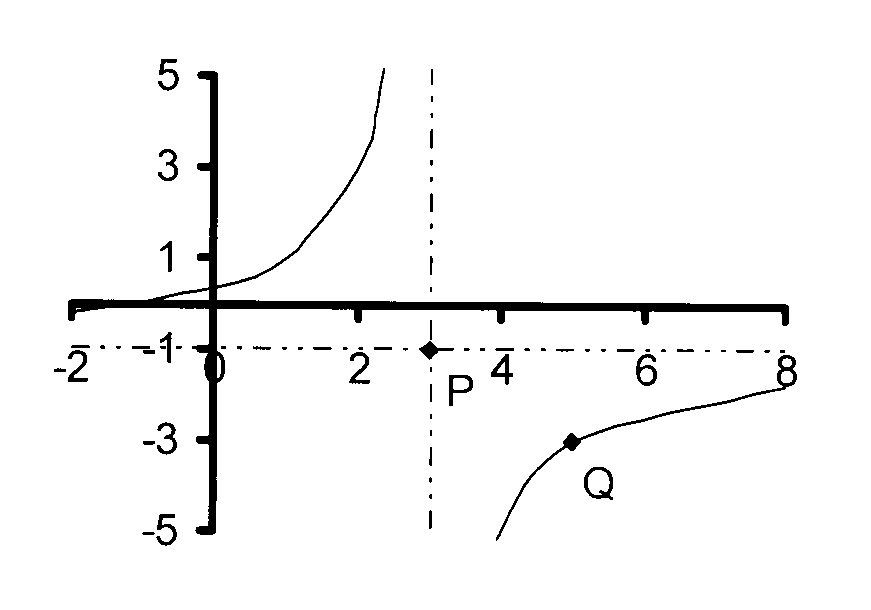
P is the point (-2 ; 4) and Q(− 3 ; 7)
P is the point (3 ; -1) and Q(5 ; −3)
3.
a
The figure shows the graph of y = ——— + q
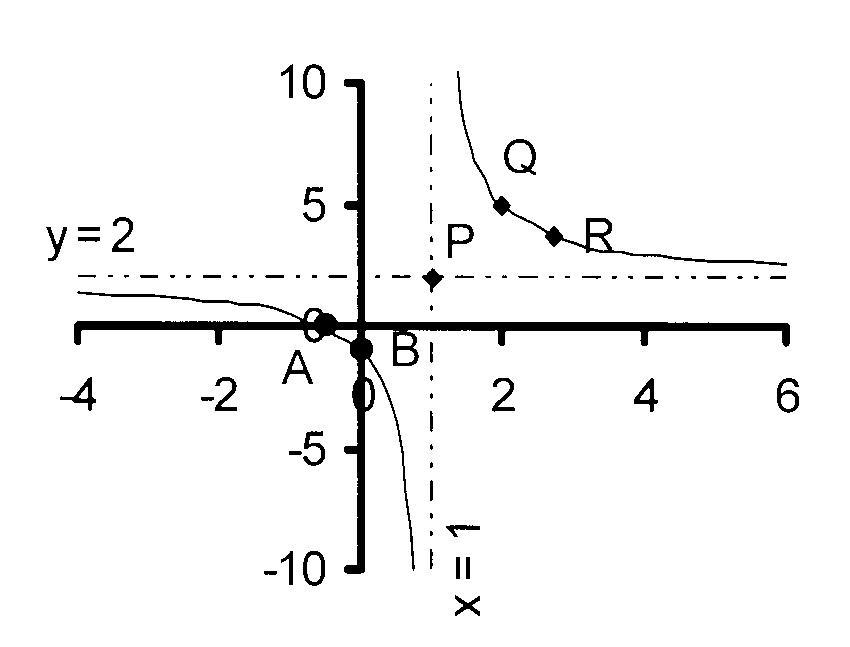
x + p
3.1
Write down the coordinates of point P.
3.2
Calculate the values of a, p and q and write down
the equation of the function given that Q(2 ; 5).
3.3
Write down the equation for the positive axis of symmetry.
3.4
Calculate the coordinates of R, the point of intersection
of the hyperbola with the axis of symmetry.
4.
a
The figure shows the graph of y = ——— + q
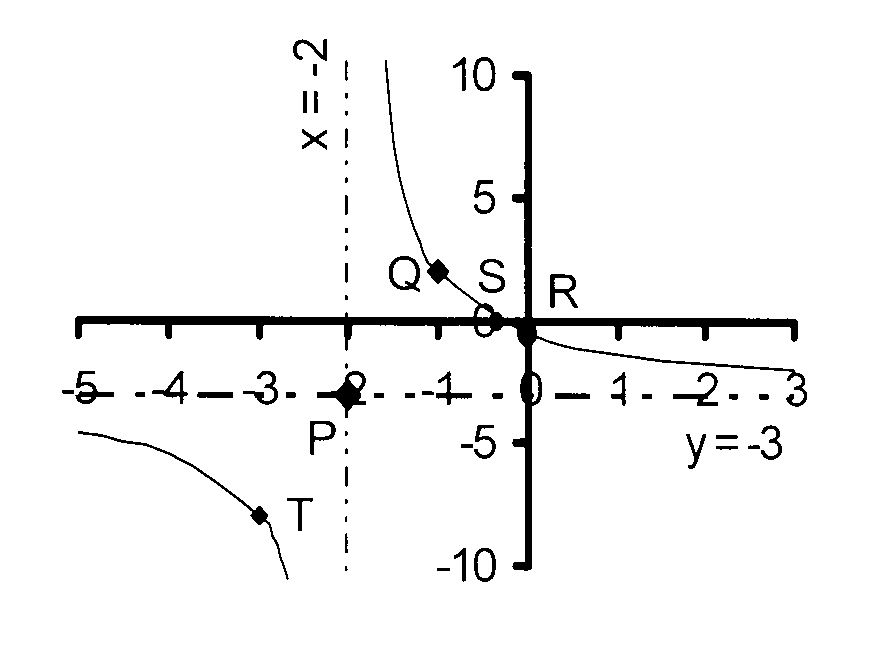
x + p
4.1
Write down the coordinates of point P.
4.2
Given that Q is the point (-1 ; 2), calculate the values
of a, p and q and write down the equation of the function.
4.3
Calculate the coordinates of A and B, the points of
intersection with the axes.
4.4
Write down the equation for the positive axis of symmetry.
4.5
Calculate the coordinates of T, the point of intersection
of the hyperbola with the axis of symmetry.
4.6
Write down the domain and range of the graph.
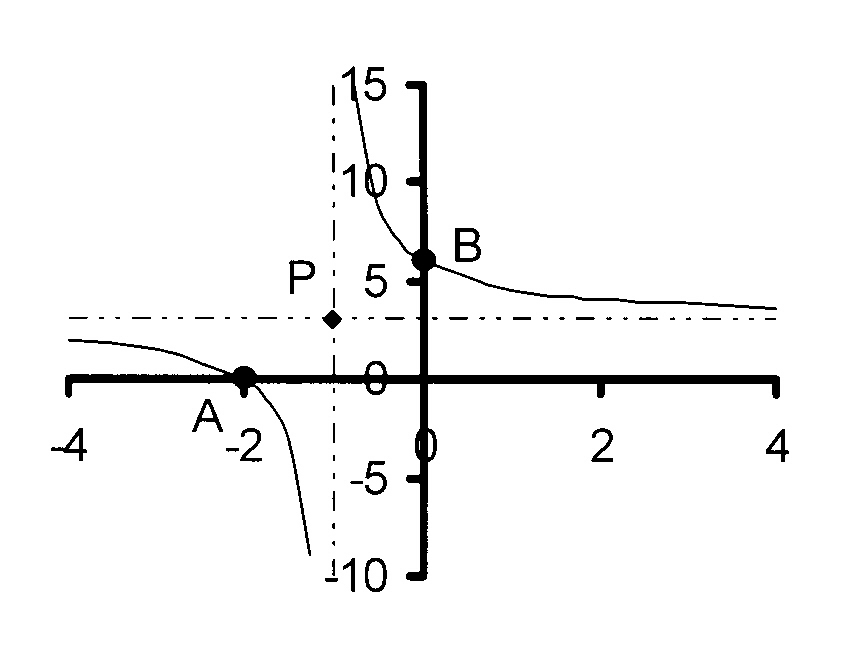
5.
a
The figure shows the graph of y = ——— + q

x + p
P is the point (2 ; 4)
5.1
Write down the equation of the horizontal asymptote.
5.2
Write down the equation of the vertical asymptote.
5.3
Given that Q is the point (-2 ; 6), calculate the values
of a, p and q and write down the equation of the function.
5.4
Calculate the coordinates of points A and B, the
intercepts with the axes.
5.5
Write down the equation for the negative axis of symmetry.
5.6
Calculate the coordinates of R and S, the points of intersection
of the hyperbola with the axis of symmetry.
5.7
Write down the domain and range of the graph.
5.8
h(x) is formed if the graph is translated 3 units downwards and 5 units to the right. Write down the equation of h(x) in the form y = . . .
6.
6
The figure shows the graph of y = 5 − ———
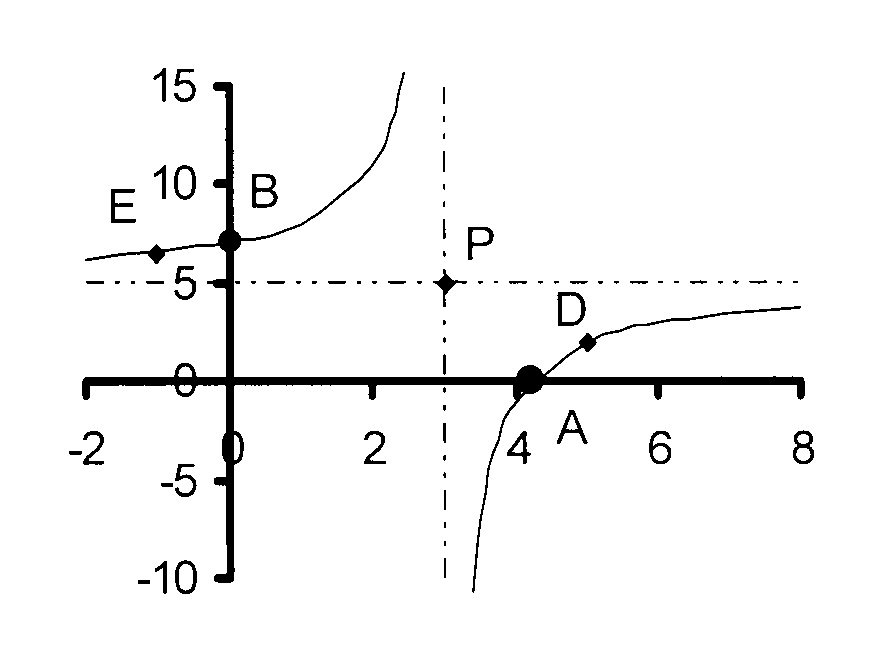
x - 3
6.1
Write down the equation of the horizontal asymptote.
6.2
Write down the equation of the vertical asymptote.
6.3
Calculate the coordinates of A, the X-intercept.
6.4
Calculate the coordinates of B, the Y-intercept.
6.5
D is the point (5 ; d). Calculate the value of d.
6.6
Calculate the value of e if E is the point (e ; 6,5)
6.7
The line y = − 2x + 15 intersects the hyperbola at points
R and S. Calculate the coordinates of the R and S.
7.
−5
The figure shows the graph of y = ——— − 3
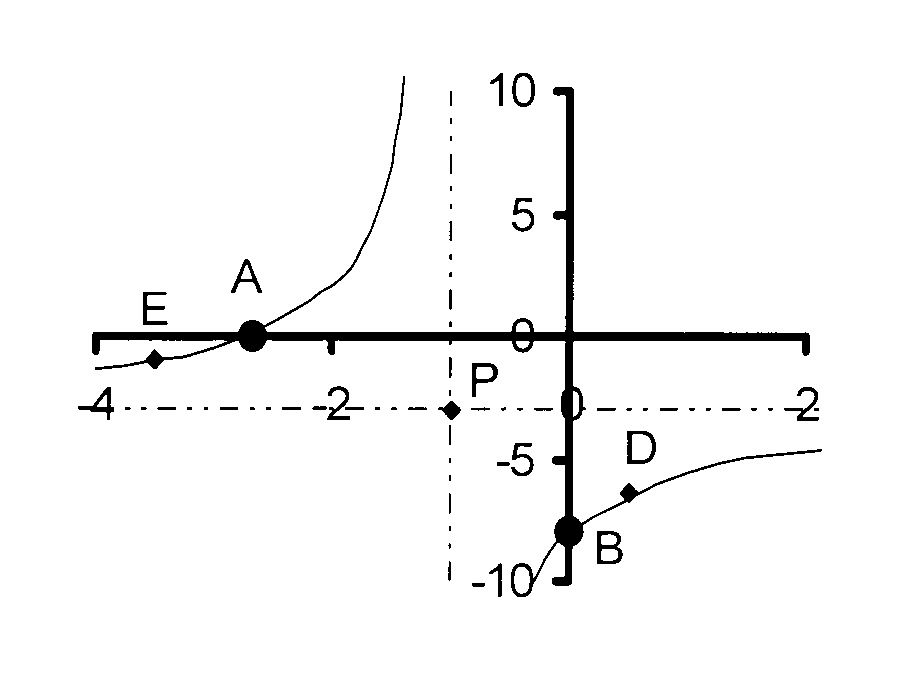
x + 1
7.1
Write down the coordinates of P, the point of
intersection of the asymptotes.
7.2
Calculate the coordinates of A, the X-intercept.
7.3
Calculate the coordinates of B, the Y-intercept.
7.4
D is the point (0,5 ; d). Calculate the value of d.
7.5
Calculate the value of e if E is the point (e ; -1)
7.6
Write down the equations for both axes of symmetry.
8.
The figure shows the parts p, q, r and s of two graphs
a
the form y = ——— + q
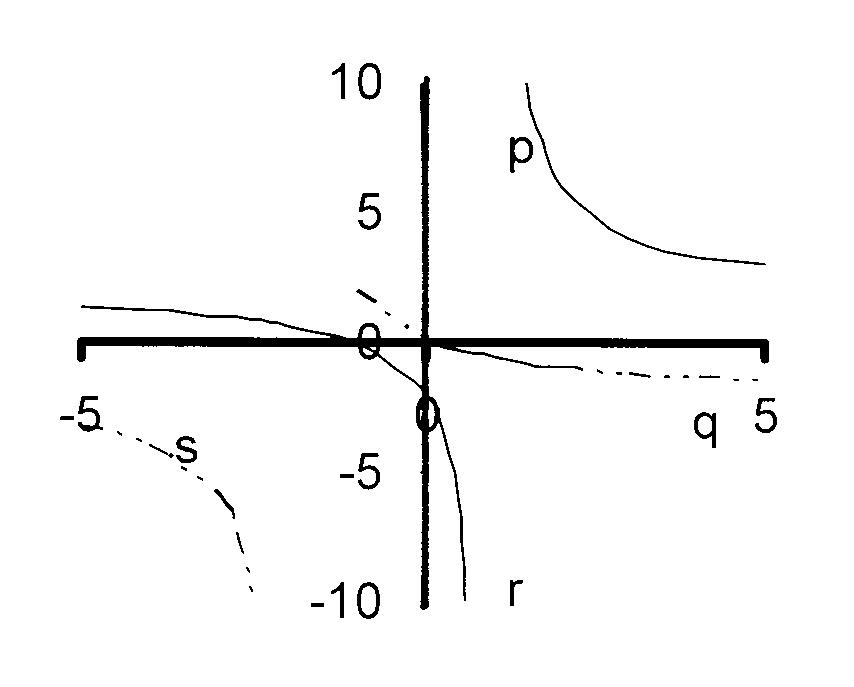
x + p
4
One graph has the equation y = ——— + 2 and
x - 1
4
the other has the equation y = ——— − 2
x + 2
8.1
Say which pieces fit which graph.
8.2
How was one graph translated to form the other?