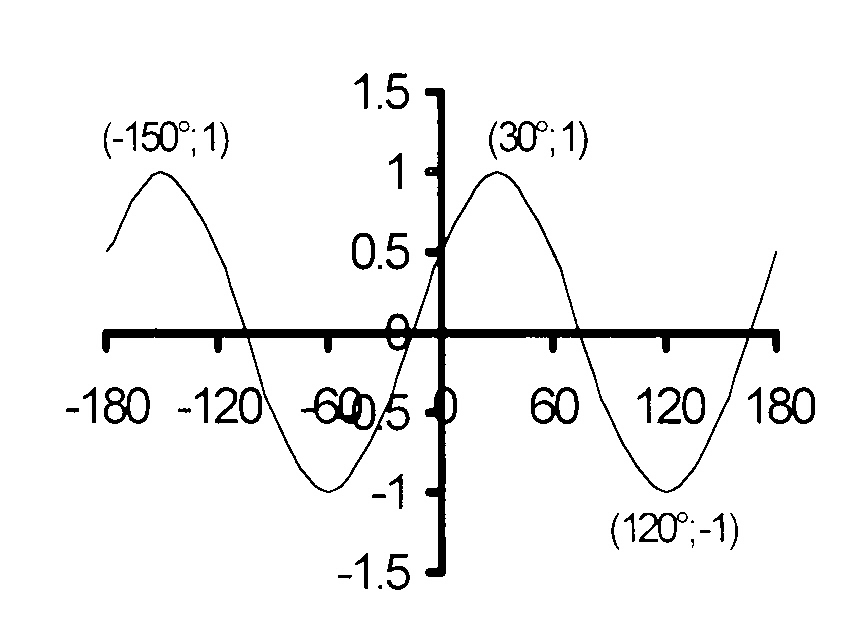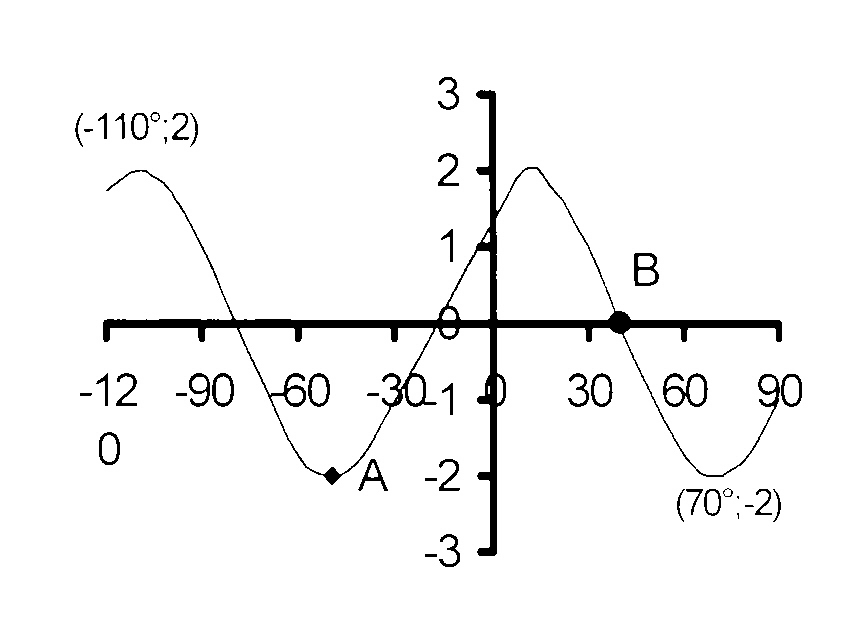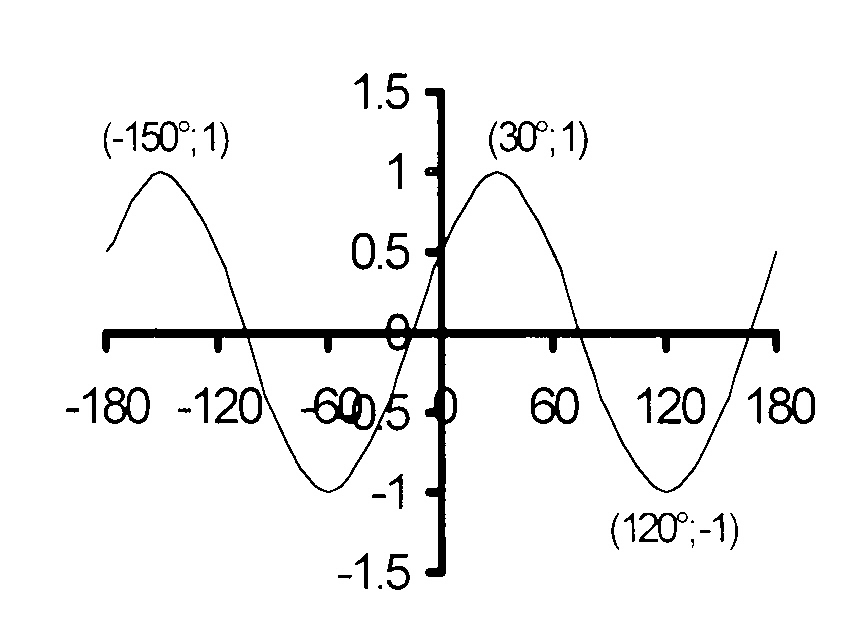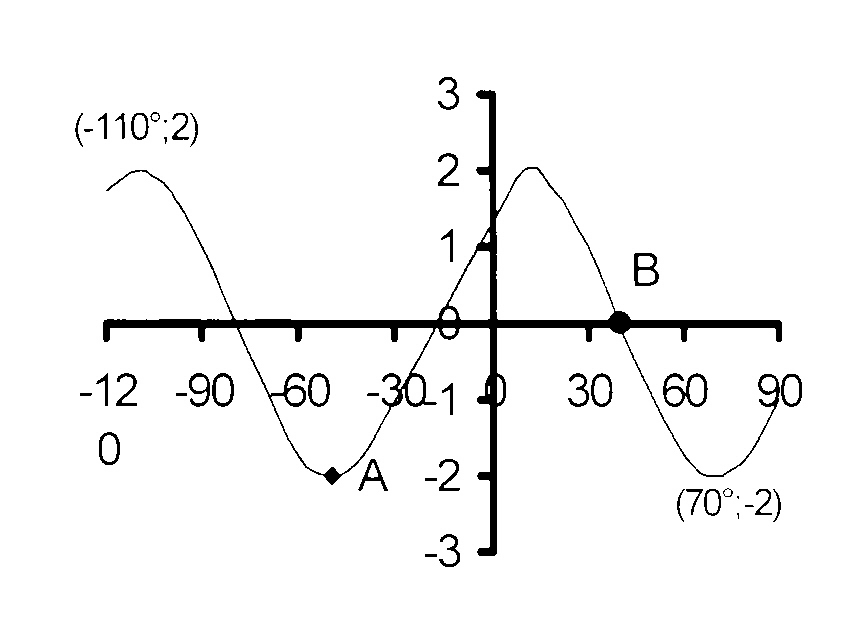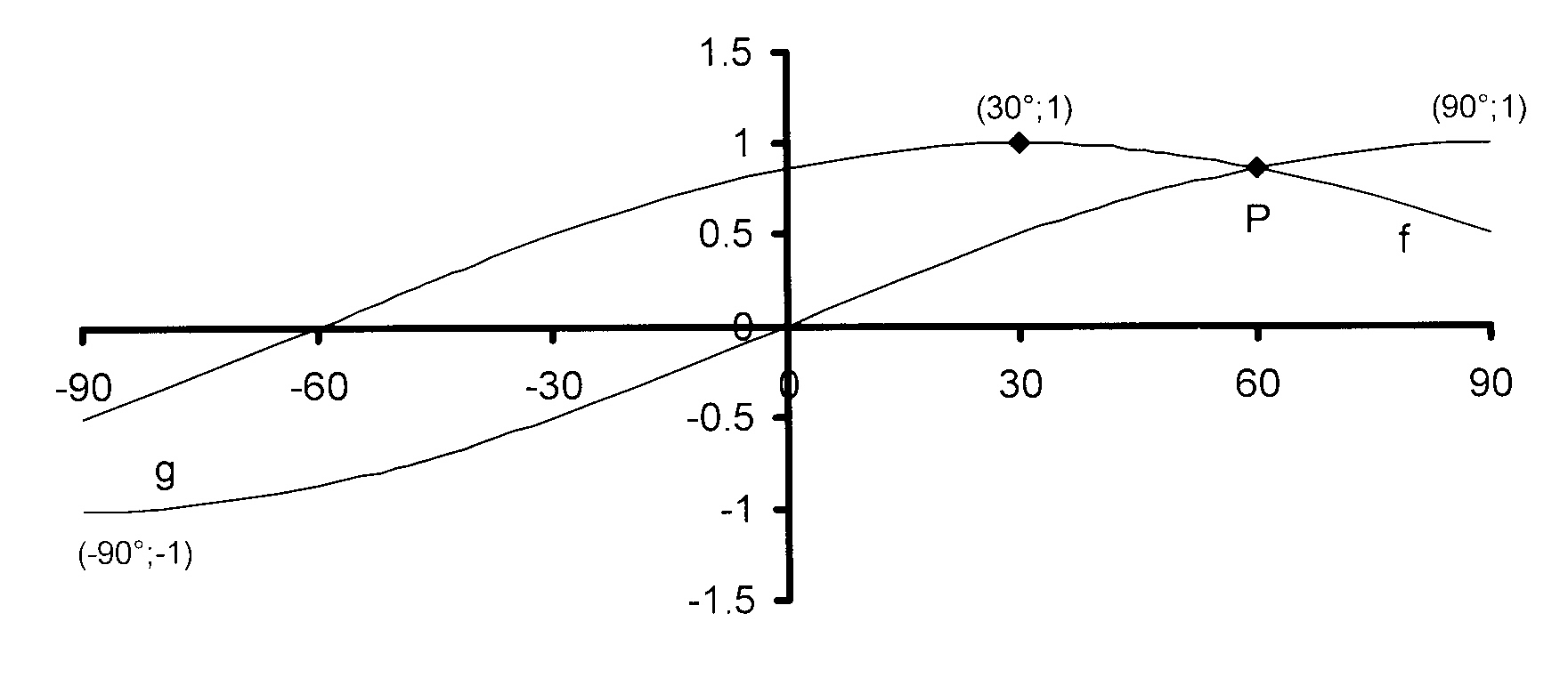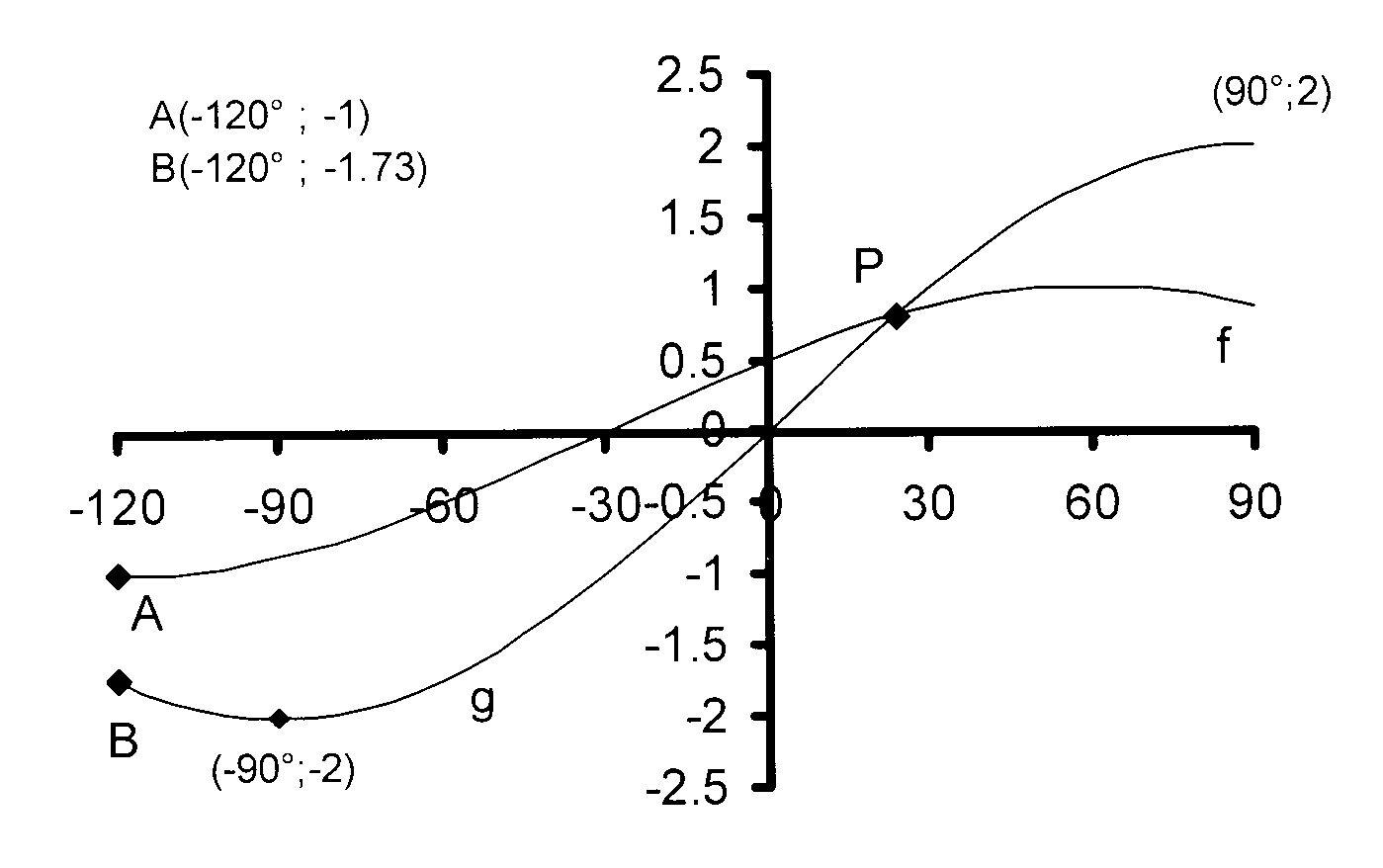Grade 11 Mathematics - More Exercises.
Graphs of sin x, cos x and tan x.
1.
Sketch the graphs of the following functions:
1.1
y = 3 cos x − 2 and x ∈ [-180° ; 180°]
1.2
y = 1 − sin x and x ∈ [-90° ; 180°]
1.3
y = cos (2x − 60°) and x ∈ [-180° ; 180°]
1.4
y = sin (x − 30°) and x ∈ [-180° ; 180°]
1.5
y = cos (x + 30°) − 1 and x ∈ [-180° ; 180°]
1.6
y = sin (x + 60°) + 1 and x ∈ [-180° ; 180°]
1.7
y = 3sin 2(x + 30°) and x ∈ [-180° ; 180°]
1.8
y = 2cos 3(x − 30°) and x ∈ [-180° ; 180°]
2.
The figures show the graphs of the trigonometric functions given at each question. Use the information
given in the figure to detemine the values of the unknown variables :
2.1 The graph of y = a sin k(x + p)
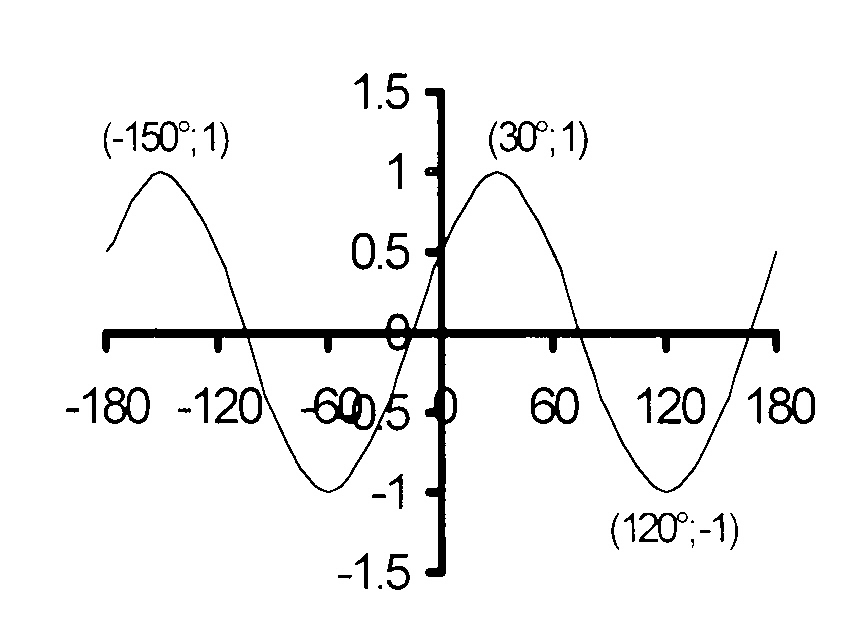
2.2 The graph of y = a cos k(x + p)
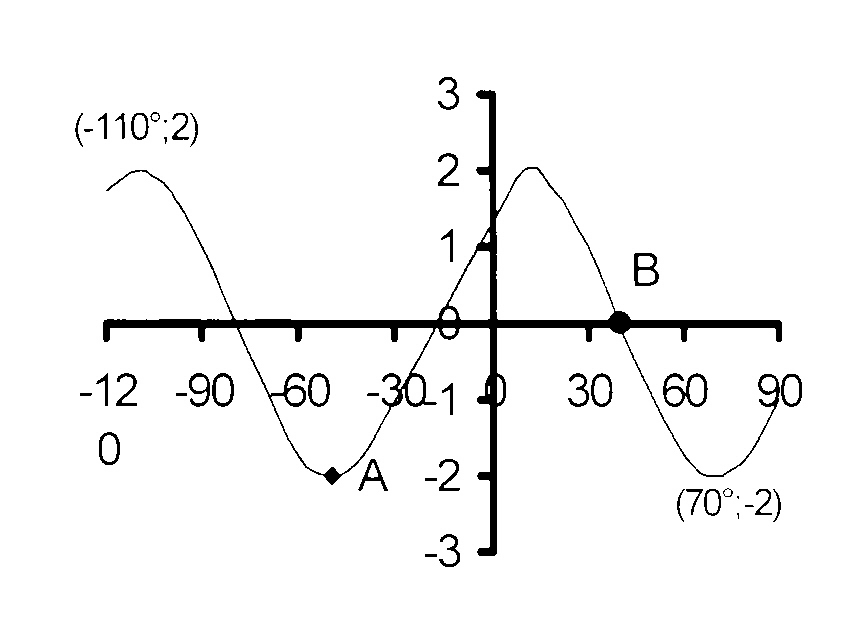
2.3 The graph of y = a sin k(x + p)
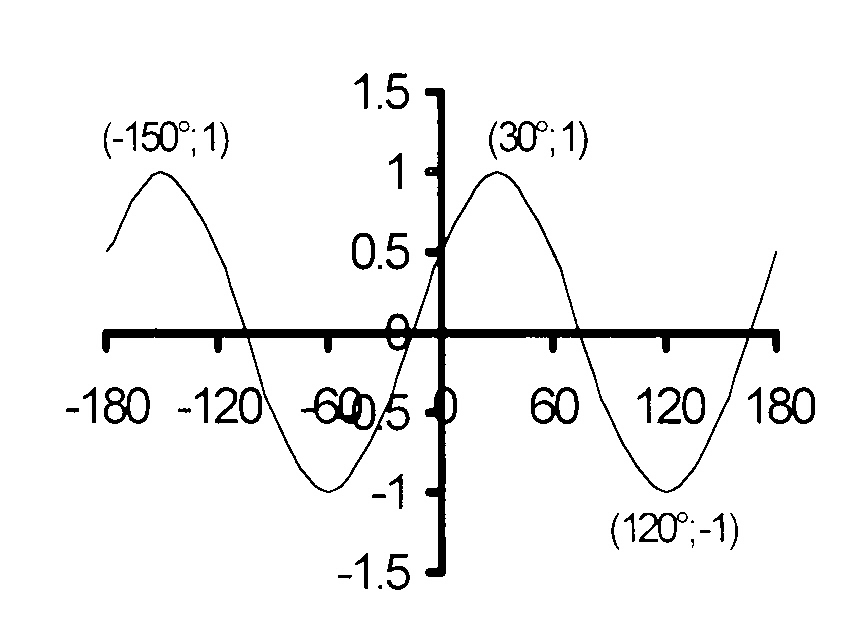
2.4 The graph of y = a cos k(x + p)
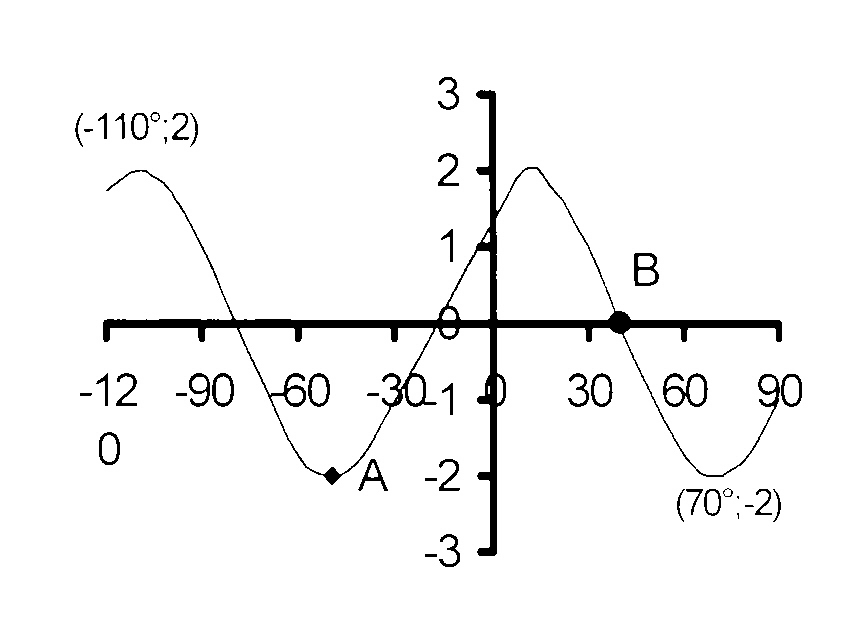
2.5 The graph of y = a sin k(x + p)
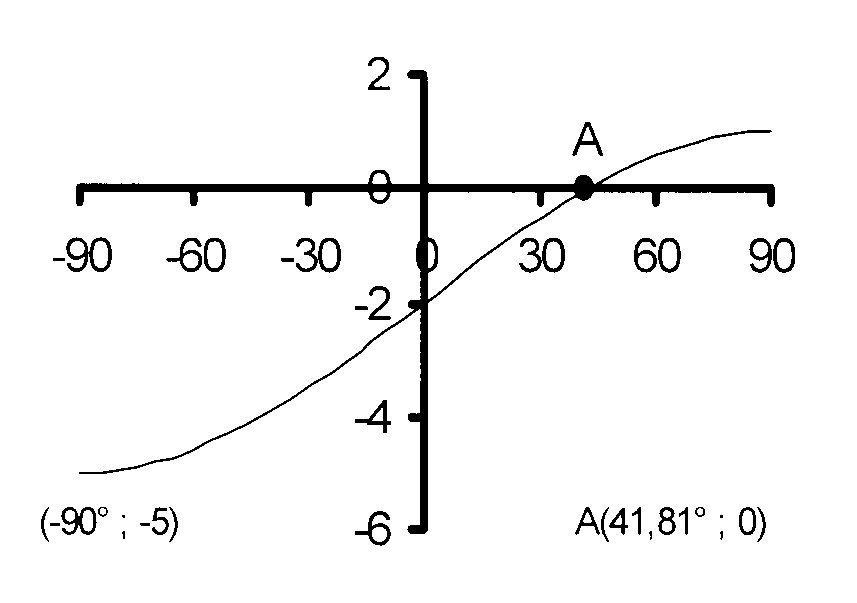
2.6 The graph of y = a cos k(x + p)
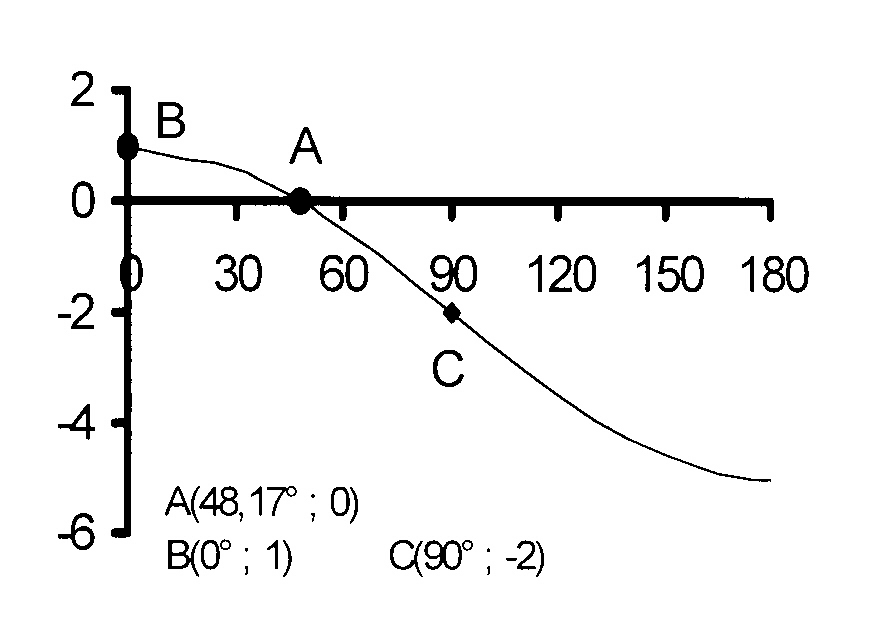
3.1
On the same set of axes draw the graphs of f(x) = sin (x − 30°) and g(x) = cos 2x for − 180° ≤ x ≤ 180°
Give the intercepts with the axes and the coordinates of the turning points. [CAPE November 1991]
3.2
Give the period of f.
3.3
Determine x by calculation if f(x) = g(x).
3.4
If the Y-axis is shifted 60° to the right, give the equation of the graph which was represented by f(x).
4.
In the figure, the graphs of f(x) = a cos (x + b) and g(x) = c + sin dx for − 180° ≤ x ≤ 180°

4.1
Determine the values of a, b, c and d
by using the graphs.
4.2
Calculate the value of f(x) if x = 0°
without using a calculator.
4.3
Determine x by using the graphs if
4.3.1
g(x) = 2
4.3.2
f(x) ≥ g(x) Q(13,5° ; 1,45)
4.4
The Y-axis is translated to pass through
the turning point of f, where f(x) reaches
a maximum. Determine an equation
for f in the form y = . . . with reference to the new set of axes.
5.
In the figure, the graphs of f(x) = a cos (x + b) and g(x) = sin cx for − 90° ≤ x ≤ 90° are given.
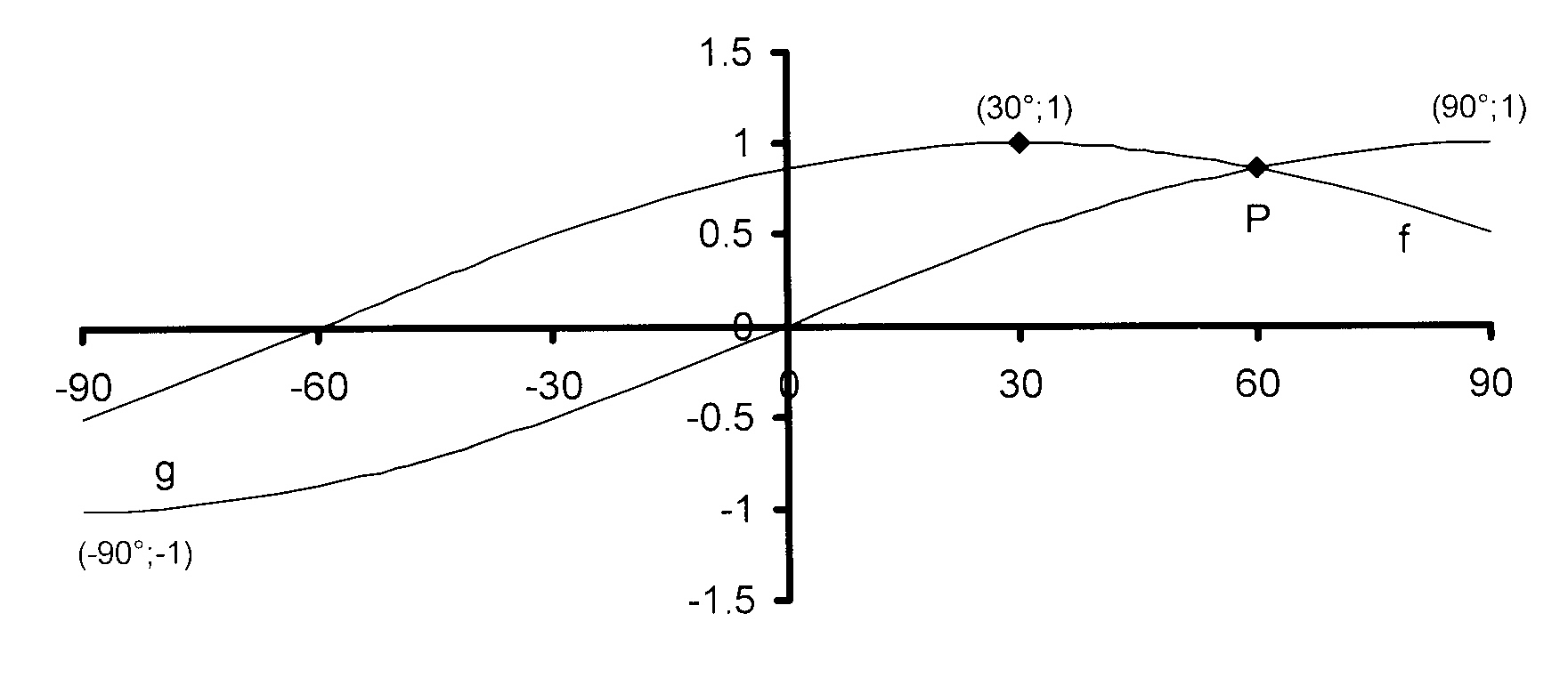
5.1
Determine the values of a, b and c.
by using the graphs.
5.2
Use the graphs to answer the following
questions:
5.2.1
Write down the range of f.
5.2.2
For what values of x is f(x) decreasing
as x increases?
5.2.3
If x ∈ [−90° ; 0°], for what
values of x is f(x).g(x) ≥ 0?
5.3
If x ∈ [−90° ; 90°], solve the equation
cos (x − 30°) = sin x and hence
write down the values of x in the interval [−90° ; 90°] for which
g(x) > f(x).
6.
In the figure, the graphs of f(x) = a cos (x + b) and g(x) = c sin dx for − 120° ≤ x ≤ 90° are given.
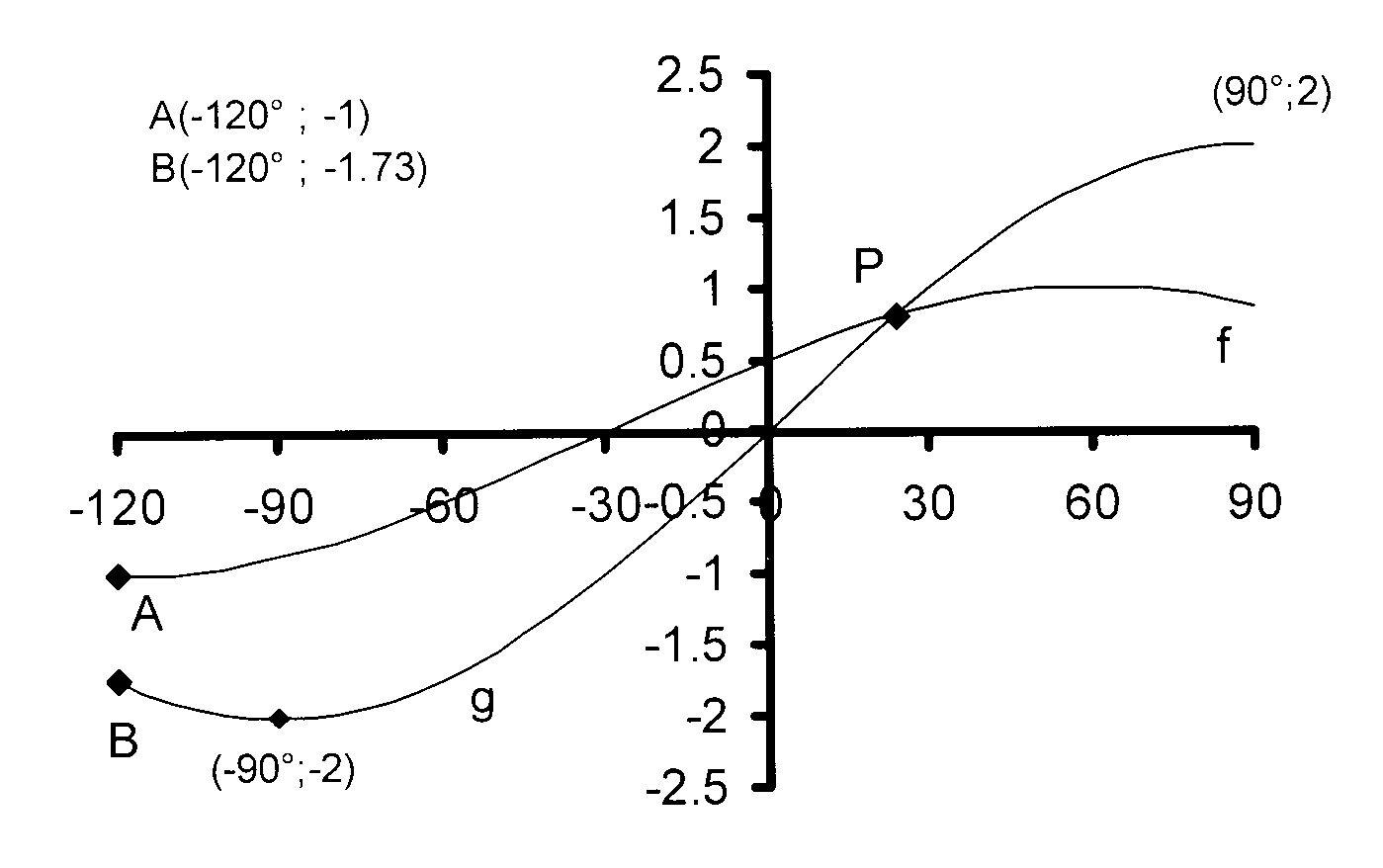
6.1
Write down the amplitude and period of g.
6.2
Determine the values of a, b, c and d.
6.3
Write down the range of g.
6.4
Write down the value(s) of x < 0° for
which f(x).g(x)≥0
6.5
If the Y-axis is moved to the left so as to
pass through the point of intersection of
the given cosine curve and the X-axis,
which function is now represented by
the curve that initially represented
the given sine function?