WISKUNDE
GRAAD 11
NOG OEFENINGE
Koordevierhoeke.
MATHEMATICS
GRADE 11
MORE EXERCISES
Cyclic quadrilaterals.
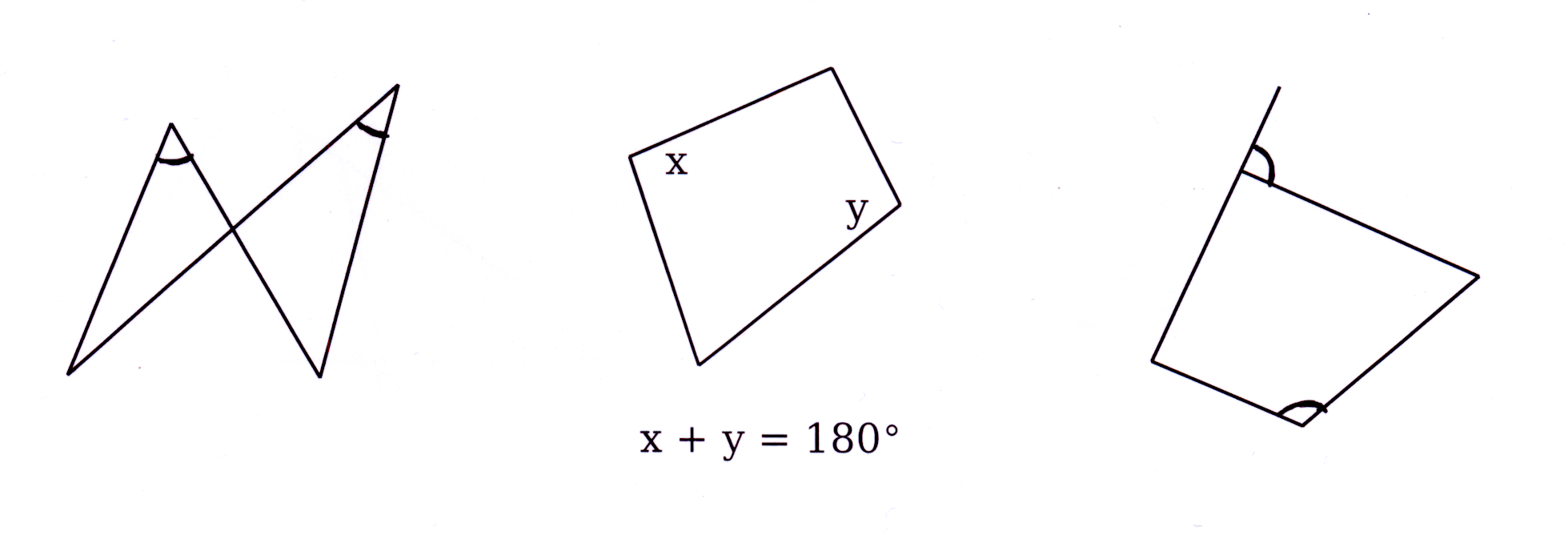
Om te be bewys dat 'n vierhoek 'n koordevierhoek is bewys dat
To prove that a quadrilateral is a cyclic quadrilateral, prove that
Vraag / Question 1.
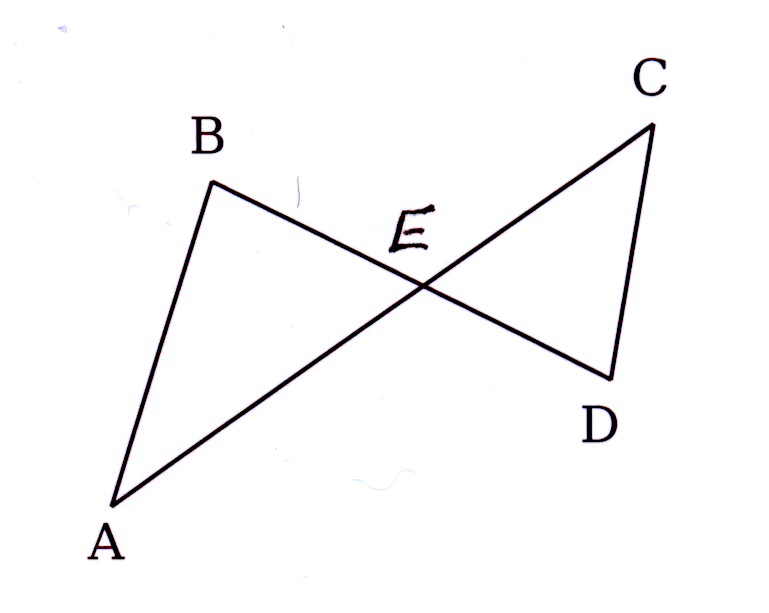
In die diagram is ∠ABC = ∠DEC = 45° en
∠ACB = 30°.
In the diagram ∠ABC = ∠DEC = 45° and
∠ACB = 30°.
Bewys dat ABDE 'n koordevierhoek is.
Prove that ABDE is a cyclic quadrilateral.
Vraag / Question 2.
In die skets is QOR die middellyn van ⊙O en ST ⊥ QOR.
In the diagram QOR is the diameter of ⊙O and ST ⊥ QOR.
Bewys punte P, S, T en R is konsiklies.
Prove points P, S, T and R are concyclic.
Vraag / Question 3.
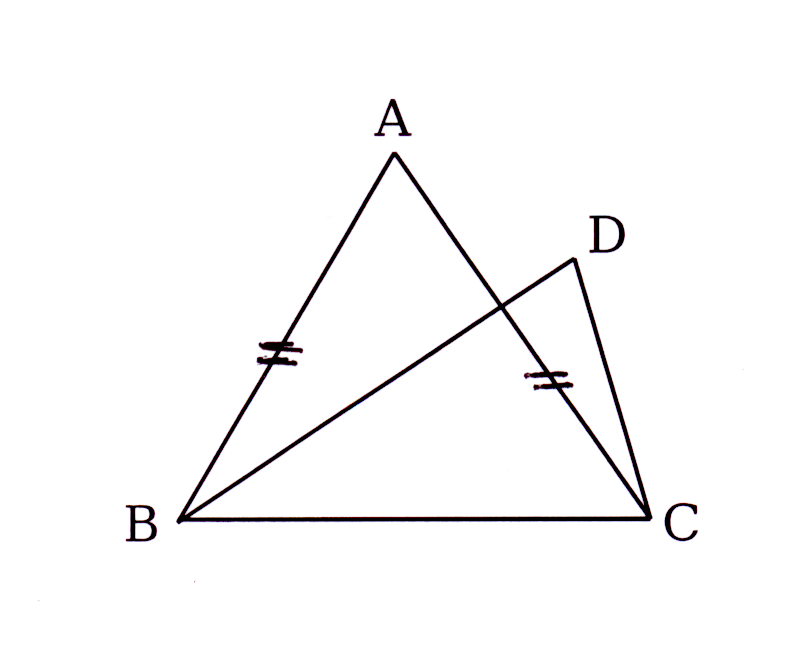
In die skets is AB || en AE = BE.
Bewys ABCD 'n koordevierhoek.
In the diagram AB || and AE = BE
Prove ABCD a cyclic quadrilateral.
Vraag / Question 4.
In die skets is ∠A = 50°, ∠C = 30°
en ∠CED = 100°.
Bewys ABCD 'n koordevierhoek.
In the diagram ∠A = 50°, ∠C = 30°
and ∠CED = 100°.
Prove ABCD a cyclic quadrilateral.
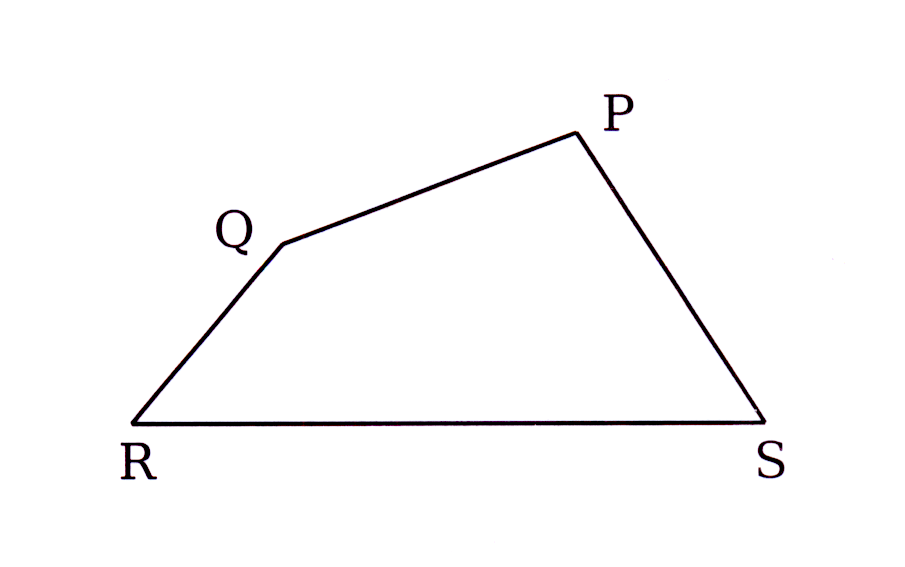
Vraag / Question 5.
In die skets is ∠P = 3x°, ∠Q = x°
∠R = 2x° en ∠S = 4x°.
Bewys PQRS 'n koordevierhoek.
In the diagram ∠P = 3x°, ∠Q = x°
∠R = 2x° and ∠S = 4x°.
Prove PQRS a cyclic quadrilateral.
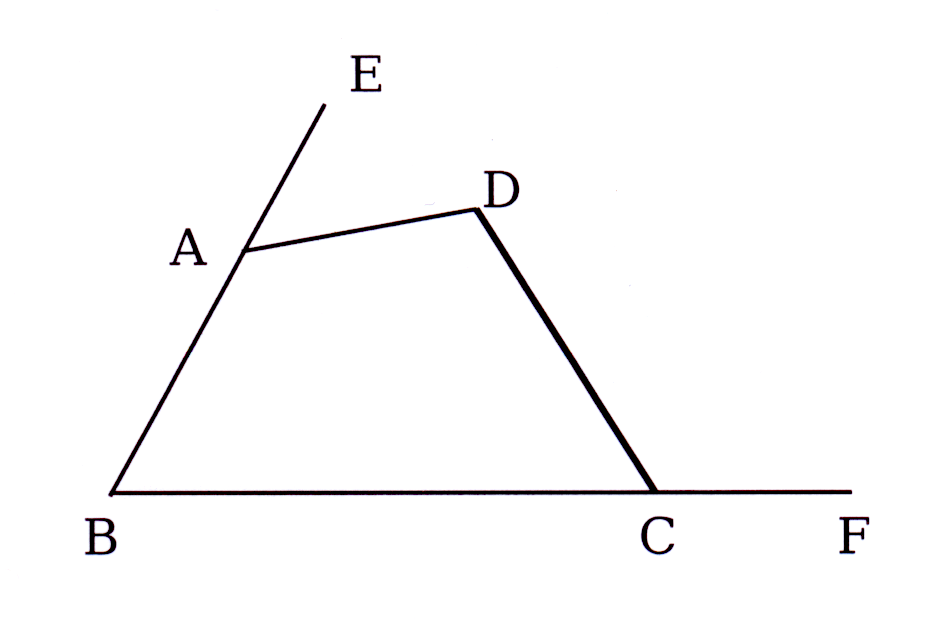
Vraag / Question 6.
In die skets is ∠DAE = 34° en ∠DCF = 146°
Bewys ABCD 'n koordevierhoek.
In the diagram ∠DAE = 34° and ∠DCF = 146°
Prove ABCD a cyclic quadrilateral.
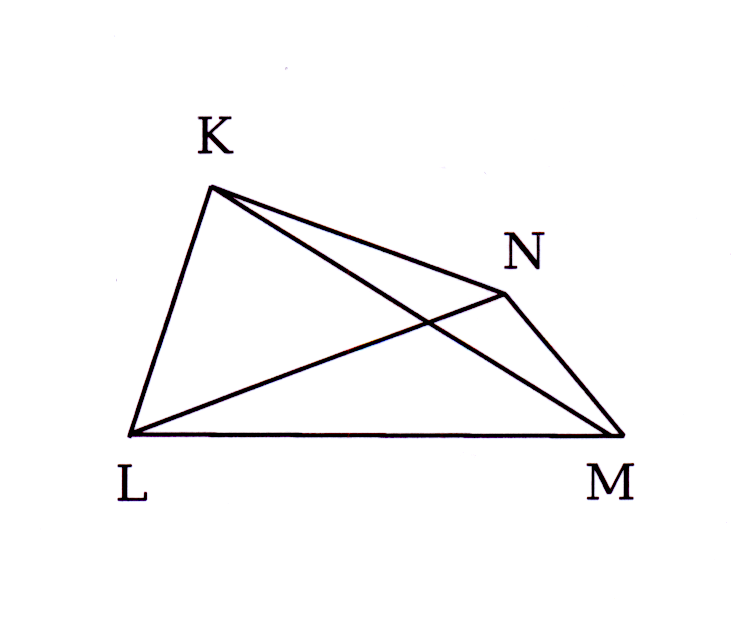
Vraag / Question 7.
In die skets is
∠NLM = 75°, ∠KMN = 35° en ∠KNM = 70°
Bewys KLMN 'n koordevierhoek.
In the diagram
∠NLM = 75°, ∠KMN = 35° and ∠KNM = 70°
Prove KLMN a cyclic quadrilateral.
Vraag / Question 8.
In die skets is AB = AC en
∠ABD = x°, ∠ACD = x°
Bewys ∠ADC = 90° + ½ ∠BAC.
In the diagram AB = AC and
∠ABD = x°, ∠ACD = x°
Prove ∠ADC = 90° + ½ ∠BAC.
Vraag / Question 9.
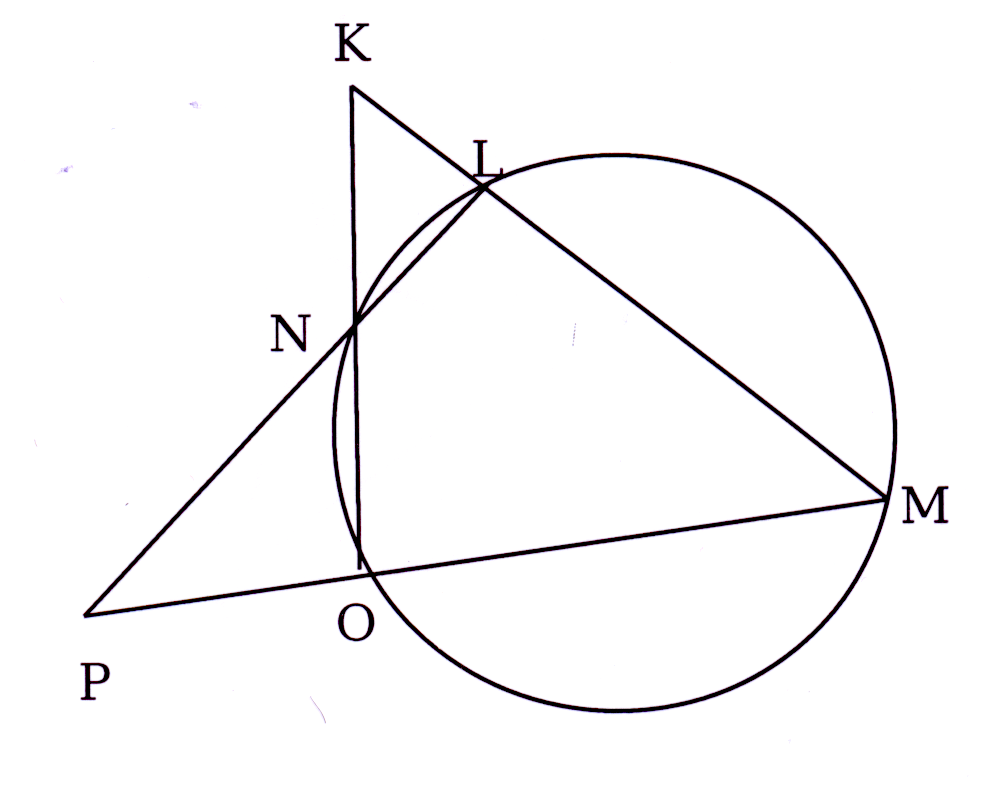
In die diagram sny MLen ON se verlengdes in K,
en LN en NO se verlengdes sny in P. ∠K = 42° en ∠P = 38°
Bereken die grootte van ∠M.
In the diagram ML and ON produced intersect at K,
and LN and MO produced intersect at P. ∠K = 42° en ∠P = 38°
Calculate the size of ∠M.
Vraag / Question 10.
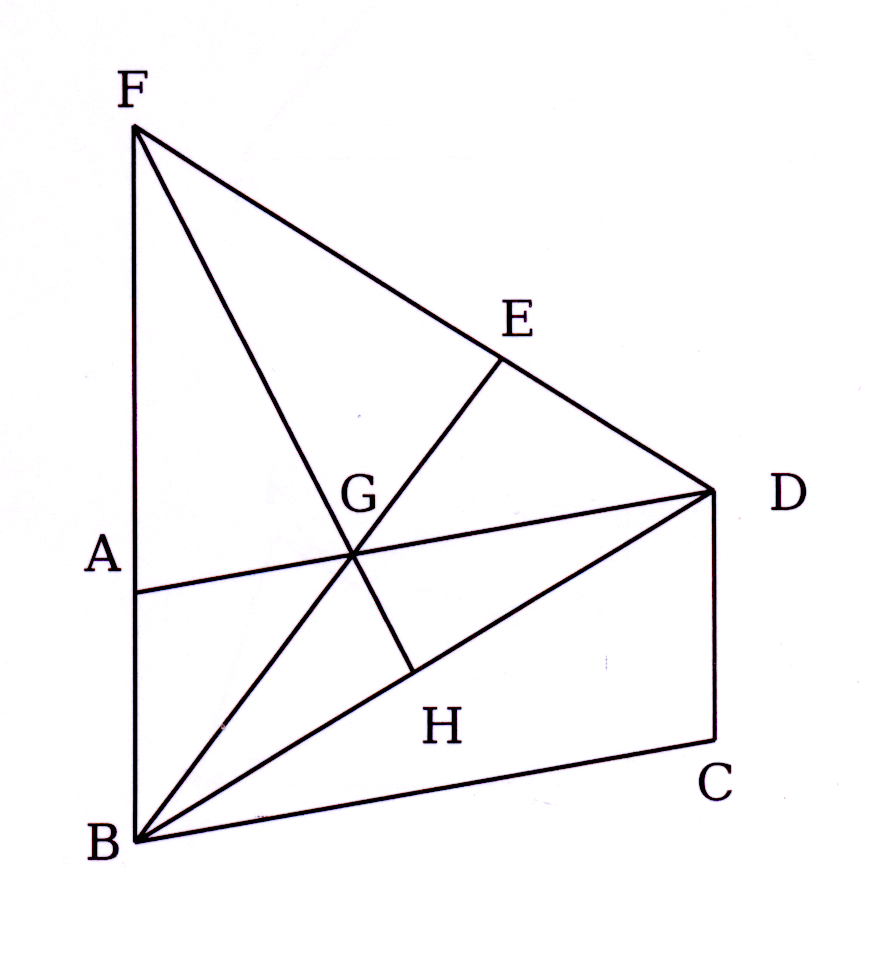
In die diagram is ABCD 'n parallelogram.
∠BDE = ∠BDC en DE = DC. DE en BA verleng,
sny in F. BE sny DA in G. FG verleng, sny BD in H.
In the diagram ABCD is a parallelogram.
∠BDE = ∠BDC and DE = DC. DE and BA
produced cut in F. BE intersects DA in G.
FG produced cuts BD in H.
Bewys / Prove
10.1
∠CBD = ∠DBE
10.2
EABD is 'n koordevierhoek. / a cyclic quadrilateral.
10.3
FA = FE
Vraag / Question 11.
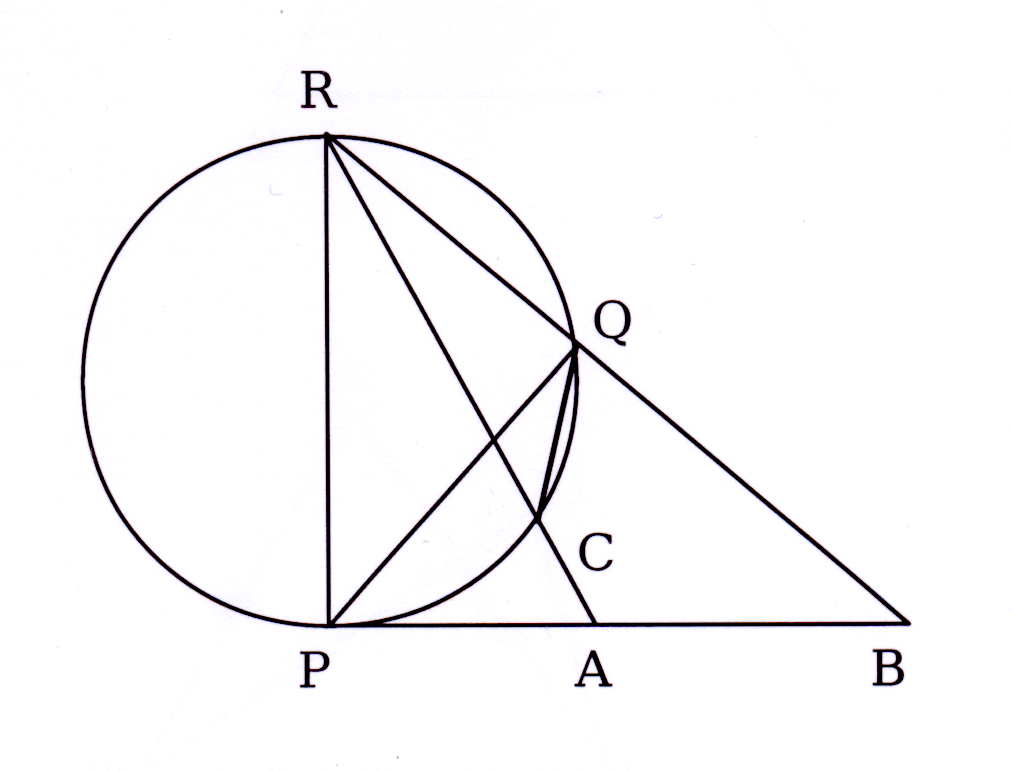
In die diagram is PR die middellyn van 'n sirkel
en PB is 'n raaklyn by P. A is die middelpunt van
PB. AR en BR sny die sirkel in C en Q
onderskeidelik.
In the diagram PR is the diameter of a circle and
PB is a tangent at P. A is the midpoint
of PB. AR and BR intersect the circles in C and Q
respectively.
Bewys dat / Prove that
11.1
∠RPQ = ∠B
11.2
ABCQ is 'n koordevierhoek. / a cyclic quadrilateral.