WISKUNDE
GRAAD 12
NOG OEFENINGE
Statistiek.
MATHEMATICS
GRADE 12
MORE EXERCISES
Statistics.
1. Die punte, uit 20, van 20 leerlinge is as volg :
15; 2; 16; 3; 7; 13; 10; 13; 3; 18; 5; 16; 7; 13;
9; 11; 6; 7; 8; 13
1. The marks, out of 20, of 20 pupils are :
15; 2; 16; 3; 7; 13; 10; 13; 3; 18; 5; 16; 7; 13;
9; 11; 6; 7; 8; 13
1.1 Bereken die volgende :
1.1.1 gemiddelde.
1.1.2 die drie kwartiele, Q1, Q2 en Q3 asook
die interkwartiel-variasie wydte.
1.1.3 die modus.
1.1.4 die standaardafwyking.
1.1 Calculate the following :
1.1.1 average.
1.1.2 the three quartiles, Q1, Q2 and Q3 as well
as the interquartile range.
1.1.3 the mode..
1.1.1 the standard deviation.
1.2 Teken 'n houer-en-puntdiagram om die
data voor te stel.
1.2 Draw a box and whisker diagram to represent
the data.
1.3 Is die data skeef? Gee 'n rede.
1.3 Is the data skewed? Giive a reason.
1.4 Hoeveel leerlinge se punt was binne
een standaardafwyking van die gemiddelde?
1.4 How many pupils had a mark within one
standard deviaton from the mean?
1.5 Vorm die data 'n normaal verspreiding?
Gee 'n rede.
1.5 Does the data form a normal distribution?
Give a reason.
1.6 Wanneer is die data positief skeef of skeef
na regs?
1.6 When is the data positively skewed or skewed
to the right?
1.7 Maak 'n netjiese skets om die mond-en-snor
diagram van positief skewe data voor te stel.
1.7 Draw a neat box and whisker diagram to
represent data that is positively skewed.
1.8 Wanneer is die data negatief skeef of skeef
na links?
1.8 When is the data negatively skewed or skewed
to the left?
1.9 Maak 'n netjiese skets om die mond-en-snor
diagram van negatief skewe data voor te stel.
1.9 Draw a neat box and whisker diagram to
represent data that is negatively skewed.
2. In die tabel hieronder stel a, b, c, d, e, f, en g
waardes in 'n datastel voor wat in toenemende
orde geskryf is. Geen waarde in hierdie stel
word herhaal nie.
2. In the table below a, b, c, d, e, f, and g represent
values in a data set written in ascending order.
No value in this data set is repeated.
Bepaal die waarde van a, b, c, d, e, f, en g as
Determine the value of a, b, c, d, e, f, and g if
* Die maksuimum waarde 54 is.
* Die variasiewydte 46 is.
* Die mediaan 37 is.
* Die verskil tussen die mediaan en die
boonste kwartiel 10 is.
* Die interkwartielvariasiewydte 32 is.
* e = 2c
* Die gemiddelde 32 is.
* The maximum value is 54.
* The range is 46.
* The median is 37.
* The difference between the median and the
upper quatile is 10.
* The interquartile range is 32.
* e = 2c
* The average is 32.
3. In die tabel hieronder stel a, b, c, d, e, f, en g
waardes in 'n datastel voor wat in toenemende
orde geskryf is. Geen waarde in hierdie stel
word herhaal nie.
3. In the table below a, b, c, d, e, f, and g represent
values in a data set written in ascending order.
No value in this data set is repeated.
Bepaal die waarde van a, b, c, d, e, f, en g as
Determine the value of a, b, c, d, e, f, and g if
* Die minimum waarde 22 is.
* Die variasiewydte 41 is.
* Die mediaan 46 is.
* Die interkwartielvariasiewydte 28 is.
* Die onderste kwartiel, Q1, is 6 groter
as die minimum.
e = c + 10
* Die gemiddelde 43 is.
* The minimum value is 22.
* The range is 41.
* The median is 46.
* The interquartile range is 28.
* The lower quartile, Q1 is 6 greater
than the minimum.
e = c + 10
* The average is 32.
4. Die lengte, in cm, van 30 Gr. 12 seuns is :
4. The length, in cm, of 30 Gr. 12 boys are :
151; 186; 152; 173; 172; 166; 174; 195; 192; 160; 188; 167; 184;
210; 153; 160; 198; 188; 200; 140; 155; 155; 188; 160; 190; 175;
180; 173; 160; 174;
4.1 Bereken die volgende :
4.1.1 gemiddelde.
4.1.2 die drie kwartiele, Q1, Q2 en Q3 asook
die interkwartiel-variasie wydte.
4.1.3 die modus.
4.1.4 die standaardafwyking.
4.1 Calculate the following :
4.1.1 average.
4.1.2 the three quartiles, Q1, Q2 and Q3 as well
as the interquartile range.
4.1.3 the mode.
4.1.1 the standard deviation.
4.2 Teken 'n houer-en-puntdiagram om die
data voor te stel.
4.2 Draw a box and whisker diagram to represent
the data.
4.3 Is die data skeef? Gee 'n rede.
4.3 Is the data skewed? Giive a reason.
4.4 Hoeveel leerlinge se punt was binne
een standaardafwyking van die gemiddelde?
4.4 How many pupils had a mark within one
standard deviaton from the mean?
4.5 Vorm die data 'n normaal verspreiding?
Gee 'n rede.
4.5 Does the data form a normal distribution?
Give a reason.
5. In die tabel hieronder word die
brandstofverbruik, in l/100 km, vir verskillende
snelhede gegee.
5. In the table below the fuel consumption,
in l/100 km, is given for different speeds.
| |
| Snelheid / Speed (km/h) | 100 |
80 | 90 |
110 | 120 |
130 | 140 |
| Verbruik / Consumption (l/110 km) | 6,0 |
4,8 | 5,5 |
6,2 | 7,0 |
7,2 | 7,8 |
|
5.1 Bereken die kleinstekwadrate-lyn vir die data.
5.1 Calculate the equation of the least squares line
for this data.
5.2 Bereken die korrelasiekoëffisiënt.
5.2 Calculate the correlation coefficient.
5.3 "Hoe hoër die spoed, hoe hoër
die brandstofverbruik". Word die bewering
deur die data gestaaf? Verklaar.
5.3 "The greater the speed, the higher the fuel
consumption". Does the data verify
this statement? Explain.
5.4 Voorspel die brandstofverbruik teen
'n spoed van 70 km/h.
5.4 Predict the fuel consumption at a speed
of 70 km/h.
5.5 Teen watter snelheid sal die brandstofverbruik
6,6 l/100 km wees?
5.5 At what speed will the fuel consumption
be 6,6 l/100 km?
6. 'n Winkelier vermoed dat jonger dames meer
aan klere per maand spandeer as ouer dames.
Hy samel die volgende inligting in :
6. A shopkeeper presumes that younger ladies spend
more per month on clothing than elder ladies.
He gathers the following information :
| |
| Ouderdom / Age (jaar/years) | 18 |
19 | 21 |
24 | 30 |
31 | 35 |
36 | 40 |
42 | 44 |
| Bedrag spandeer / Amount spent (R) | 300 |
320 | 320 |
260 | 230 |
200 | 190 |
170 | 130 |
110 | 100 |
|
6.1 Bereken die kleinstekwadrate-lyn vir die data.
6.1 Calculate the equation of the least squares line
for this data.
6.2 Bereken die korrelasiekoëffisiënt.
6.2 Calculate the correlation coefficient.
6.3 Bevestig die data die winkellier se
vermoede? Verklaar.
6.3 Is the shopkeeper's presumption supported
by the data? Explain.
6.4 Voorspel die bedrag wat 'n 20 jarige
dame sal spandeer.
6.4 Predict the amount spent by a 20 year
old lady.
6.5 Voorspel die ouderdom van 'n dame
wat R210 per maand spandeer.
6.5 Predict the age of a ladt that spends
R210 per month.
7. Die massa van 30 Gr. 12 leerlinge word in
onderstaande tabel opgesom.
7. The table below summarises the mass of 30
Gr. 12 pupils.
| |
| Massa m (kg)
Mass m (kg) |
Klas middelpunt
Class midpoint |
Frekwensie f
Frequency |
Kum. frek.
Cum. freq. |
f . x |
| 50 < m ≤ 60 |
55 |
3 | 3 |
|
| 60 < m ≤ 70 |
|
7 | 10 |
|
| 70 < m ≤ 80 |
|
9 | |
|
| 80 < m ≤ 90 |
|
7 | |
|
| 90 < m ≤ 100 |
|
3 | |
|
| 100 ≤ m ≤ 110 |
|
1 | |
|
|
7.1 Voltooi die tabel.
7.1 Complete the table.
7.2 Bereken die gemiddelde.
7.2 Calculate the mean.
7.3 Teken 'n ogief vir die massa van die leerlinge.
7.3 Draw an ogive for the mass of the pupils.
7.4 Gebruik die ogief om die drie kwartiele
te bereken.
7.4 Use the ogive to calculate the three quartiles.
8. Die punte, uit 100, van 50 Gr. 12 leerlinge word in
onderstaande tabel opgesom.
8. The table below summarises the marks, out of 100,
of 50 Gr. 12 pupils.
| |
| Punte
Marks |
Klas middelpunt
Class midpoint |
Frekwensie f
Frequency |
Kum. frek.
Cum. freq. |
f . x |
| 0 ≤ m ≤ 10 |
5 |
2 | 4 |
|
| 10 < m ≤ 20 |
|
3 | |
|
| 20 < m ≤ 30 |
|
4 | |
|
| 30 < m ≤ 40 |
|
5 | |
|
| 40 < m ≤ 50 |
|
8 | |
|
| 50 < m ≤ 60 |
|
8 | |
|
| 60 < m ≤ 70 |
|
7 | |
|
| 70 < m ≤ 80 |
|
6 | |
|
| 80 < m ≤ 90 |
|
4 | |
|
| 90 < m ≤ 100 |
|
3 | |
|
|
8.1 Voltooi die tabel.
8.1 Complete the table.
8.2 Bereken die gemiddelde.
8.2 Calculate the mean.
8.3 Hoeveel leerlinge het minder as 40 punte?
8.3 How many pupils have less that 40 marks?
8.4 Hoeveel leerlinge het meer as 39 maar minder
as 61 punte?
8.4 How many pupils have more than 39 but less
than 61 marks?
8.5 Teken 'n ogief vir die massa van die leerlinge.
8.5 Draw an ogive for the mass of the pupils.
8.6 Gebruik die ogief om die drie kwartiele
te bereken.
8.6 Use the ogive to calculate the three quartiles.
8.7 Wat is die maksimum punt van die onderste
25% van die leerlinge?
8.7 What is the maximum mark for the bottom
25% of the pupils?
8.8 Wat is die minimum punt van die boonste
25% van die leerlinge?
8.8 What is the minimum mark for the top
25% of the pupils?
8.9 Teken die mond-en-snor diagram om die data
voor te stel as die minimum punt 4 en
die maksimum 96 is.
8.9 Draw the box and whisker diagram to represent
the data if the minimum mark is 4 and the
maximum is 96.
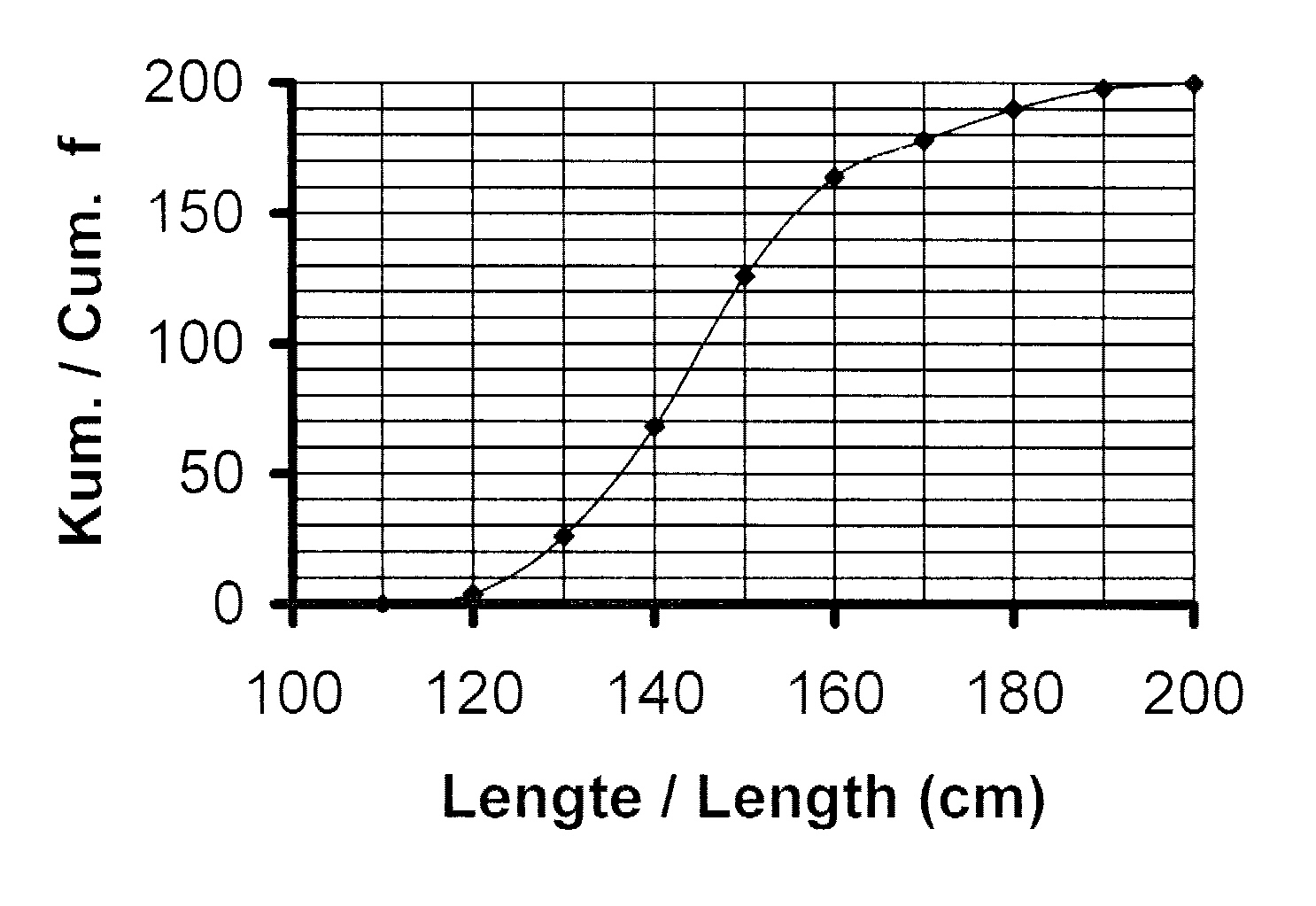
9. Die ogief langsaan toon die lengte van
200 skoliere.
9.1 Hoeveel leerlinge se lengte is tussen
140 cm en 170 cm?
9.2 Hoeveel leerlinge is korter as 160 cm?
9.3 Bereken Q1, Q2 en Q3.
9.4 Wat is die maksimum lengte van die kortste
25% van die skoliere?
9.5 Wat is die miniimum lengte van die langste
25% van die skoliere?
9.6 Teken 'n netjiese mond-en-snor diagram om
die vyfpunt voorstelling van die data voor te
stel as die minimum lengte 112 cm en die
maksimum lengte 196 cm is.
9. The ogive at the top shows the length of 200 scholars.
9.1 How many scholars are taller than 140 cm but shorter than 170 cm?
9.2 How many scholars are shorter than 160 cm?
9.3 Calculate Q1, Q2 en Q3.
9.4 What is the maximum length of the shortest 25% of the scholars?
9.5 What is the minimum length ot the taller 25% of the scholars?
9.6 Draw a neat box and whisker diagram to represent the five point summary of the data if the
minimum length is 112 cm and the maximum length is 196 cm.
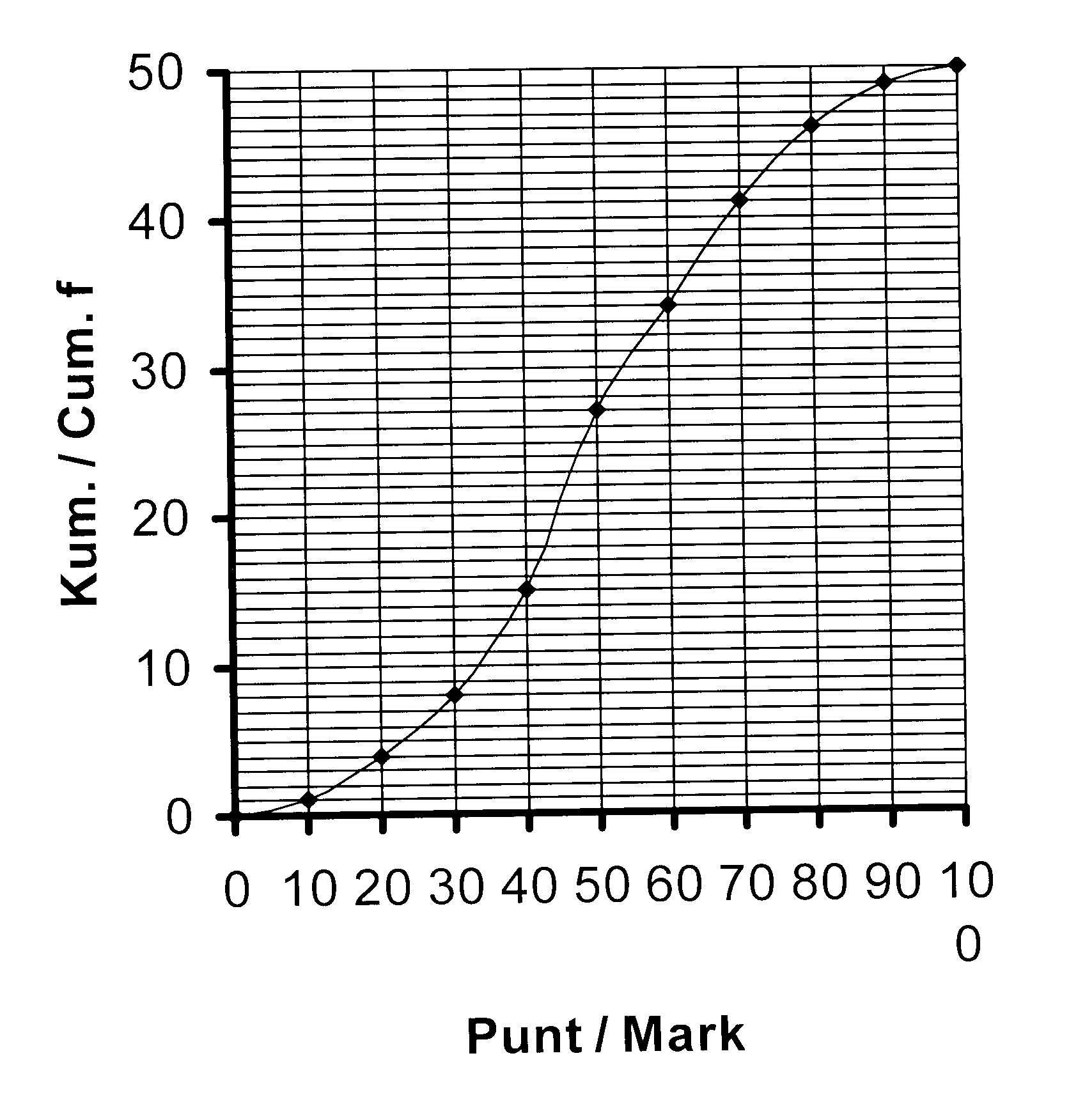
10. Die kumulatiewefrekwensie-kromme
langsaan toon die punte wat 'n aantal
studente in 'n eksamen behaal het.
10.1 Hoeveel studente het die eksamen
afgelê?
10.2 Veertig persent van die studente het
gedruip. Bepaal die slaagpunt.
10.3 Bereken Q1, Q2 en Q3.
10.4 Hoeveel studente het 'n punt
tussen 48 en 65?
10.5 Teken 'n netjiese mond-en-snor
diagram om die inligting voor te
stel as die minimum punt 7 en die
maksimum punt 97 is.
10. Die cumulative frequency curve at the top shows the marks obtained in an examination by a number
of students.
10.1 How many students wrote the examination?
10.2 Forty percent of the students failed. Calculate the pass mark.
10.3 Calculate Q1, Q2 en Q3.
10.4 How many students obtained a mark between 48 and 65?
10.5 Draw a neat box and whisker diagram to represent the data if the minimum mark is 7 cm and
the maximum mark is 97.
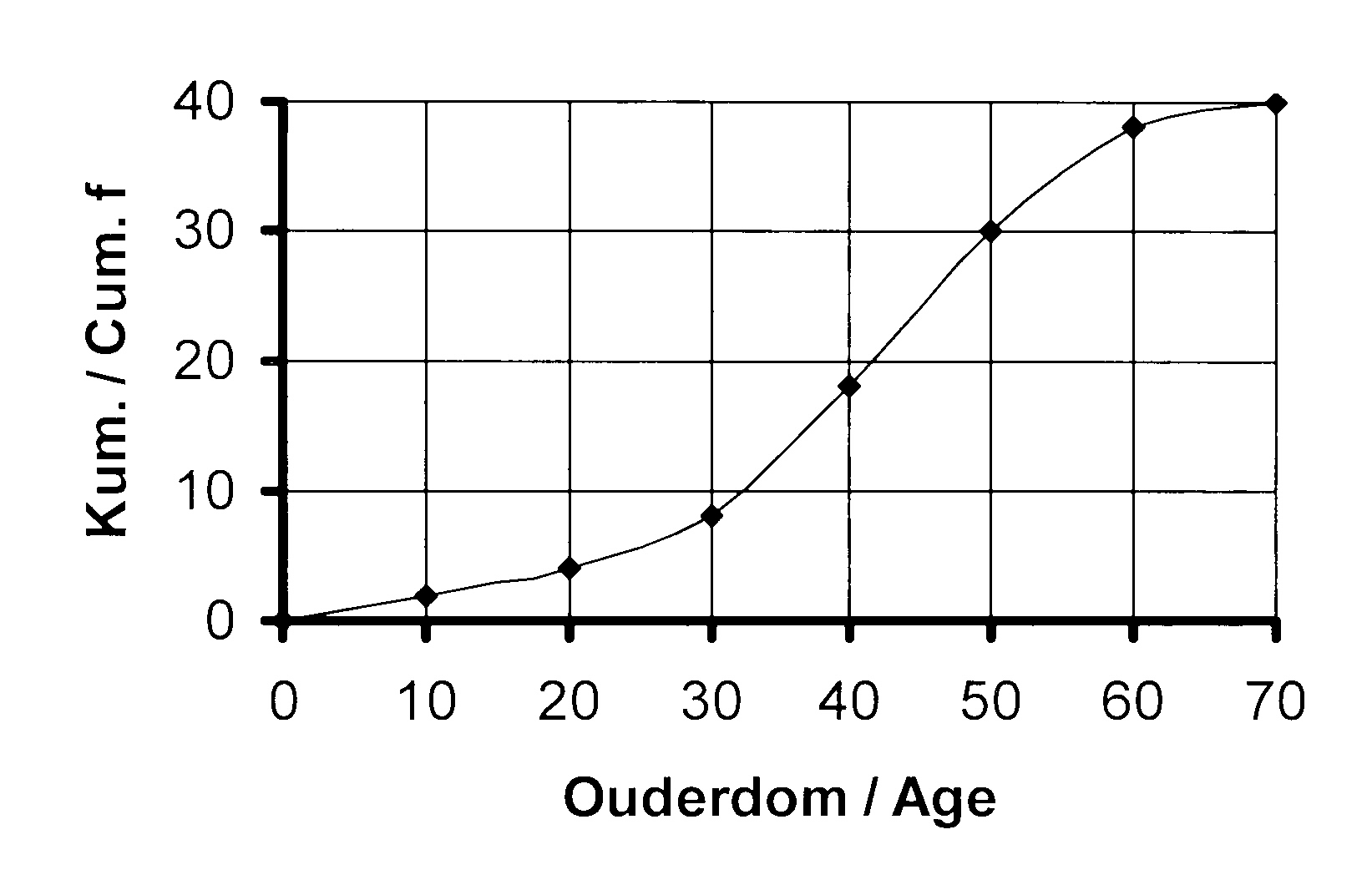
11. Die kumulatiewefrekwensie-kromme langsaan
toon die ouderdom van 'n aantal mense
in 'n winkel.
11.1 Hoeveel mense was daar in die winkel?
11.2 Bereken Q1, Q2 en Q3.
11.3 Wat is die mediaan ouderdom van die mense?
11.4 Teken 'n netjiese mond-en-snor diagram om
die inligting voor te stel as die jongste
persoon 4 en die oudste persoon 68 is.
11. The accompanying cumulative frequency curve
shows the ages of a number of shoppers in a shop.
11.1 How many shoppers were in the shop?
11.2 Calculate Q1, Q2 en Q3.
11.3 What is the median age of the shoppers?
11.5 Draw a neat box and whisker diagram to represent the data if the youngest shopper is 7 and
the eldest shopper is 68.
12. Die tabel toon die molêre massa, in g.mol−1,
en die kookpunte, in °C; van 'n aantal
chemiese verbindings.
12. The table shows the molar mass, in g.mol−1,
and the boiling points, in °C, of a number of
chemical compounds.
| |
| Molêre massa g.mol−1 (m)
Molar mass g.mol−1 (m) |
16 | 30 |
58 | 92 |
100 | 128 |
170 | 184 |
| Kookpunt °C (T)
Boiling point °C (T) |
− 162 | − 88 |
− 0,5 | 36 |
98 | 151 |
214 | 232 |
|
12.1 Bepaal die vergelyking van die
kleinstekwadrate lyn.
12.1 Determine the equation of the smallest
squares line.
12.2 Bereken die korrelasie koëffisiënt.
12.2 Calculate the correlation coefficient..
11.3 Beskryf die verhouding tussen die molêre
massa en die kookpunt van 'n stof.
12.3 Describe the relationship between the molar
mass and the boiling point of a compound.
12.4 Voorspel die kookpunt van 'n verbinding
met molêre massa 44 g.mol−1.
12.4 Predict the boiling point of a compound with
molar mass equal to 44 g.mol−1.
12.5 Voorspel die molêre massa, in g.mol−1,
van 'n stof met kookpunt 98 °C.
12.5 Predict the molar mass, in g.mol−1. of
a substance if its boiling point is 98 °C.
13. Die kleinstekwadrate regressie lyn wat die
verwantskap tussen die veranderlikes x en y
toon, word gegee deur y = 30 + 2,8x
13. The least squares regression line that shows the
relationship between the veriables x and y, is
given by y = 30 + 2,8x
13.1 Beskryf die verhouding tussen x en y.
13.1 Describe the relationship between x and y.
13.2 Voorspel y as x = 21.
13.2 Predict y if x = 21.
13.3 Voorspel x as y = 85.
13.3 Predict x if y = 85.
14. Die kleinstekwadrate regressie lyn wat die
verwantskap tussen die veranderlikes x en y
toon, word gegee deur y = 64 − 1,5x
14. The least squares regression line that shows the
relationship between the veriables x and y, is
given by y = 64 − 1,5x
14.1 Beskryf die verhouding tussen x en y.
14.1 Describe the relationship between x and y.
14.2 Voorspel y as x = 13.
14.2 Predict y if x = 13.
14.3 Voorspel x as y = 5.
14.3 Predict x if y = 5.