WISKUNDE
GRAAD 12
NOG OEFENINGE
Omtrek, oppervlakte en volume
GRAAD 12
NOG OEFENINGE
Omtrek, oppervlakte en volume
MATHEMATICS
GRADE 12
MORE EXERCISES
Perimeter, area and volume
GRADE 12
MORE EXERCISES
Perimeter, area and volume
Bereken die oppervlakte van die volgende 2D
2D figure:
1.1 'n reghoek met lengte = 20 cm en
breedte = 120 mm. [ A 1.1 ]
1.2 'n reghoekige driehoek met die
reghoeksye 45 cm en 31 cm. [ A 1.2 ]
1.3 'n driehoek met basis 30 m en
hoogte 5,5 m. [ A 1.3 ]
1.4 'n parallelogram met sy 18 mm
en hoogte 8 mm. [ A 1.4 ]
1.5 'n gelykbenige driehoek met
basis 38 cm en hoogte 18 cm. [ A 1.5 ]
1.6 'n gelyksydige driehoek met
sy 56 m en hoogte 46,4 m. [ A 1.6 ]
1.7 'n sirkel met radius 23,4 cm. [ A 1.7 ]
1.8 'n sirkel met middellyn 4,65 m. [ A 1.8 ]
2D figure:
1.1 'n reghoek met lengte = 20 cm en
breedte = 120 mm. [ A 1.1 ]
1.2 'n reghoekige driehoek met die
reghoeksye 45 cm en 31 cm. [ A 1.2 ]
1.3 'n driehoek met basis 30 m en
hoogte 5,5 m. [ A 1.3 ]
1.4 'n parallelogram met sy 18 mm
en hoogte 8 mm. [ A 1.4 ]
1.5 'n gelykbenige driehoek met
basis 38 cm en hoogte 18 cm. [ A 1.5 ]
1.6 'n gelyksydige driehoek met
sy 56 m en hoogte 46,4 m. [ A 1.6 ]
1.7 'n sirkel met radius 23,4 cm. [ A 1.7 ]
1.8 'n sirkel met middellyn 4,65 m. [ A 1.8 ]
Calculate the area of the following 2D figures :
1.1 a rectangle with length = 20 cm and
width = 120 mm. [ A 1.1 ]
1.2 a right-angled triangle with the
right-angled sides equal to 45 cm
and 31 cm. [ A 1.2 ]
1.3 a triangle with base 30 m and
height 5,5 m. [ A 1.3 ]
1.4 a parallelogram with length 18 mm
and height 8 mm. [ A 1.4 ]
1.5 an isosceles triangle with base
38 cm and height 18 cm. [ A 1.5 ]
1.6 an equlateral triangle with side
56 m and height 46,4 m. [ A 1.6 ]
1.7 a circle with radius 23,4 cm. [ A 1.7 ]
1.8 a circle with diameter 4,65 m. [ A 1.8 ]
1.1 a rectangle with length = 20 cm and
width = 120 mm. [ A 1.1 ]
1.2 a right-angled triangle with the
right-angled sides equal to 45 cm
and 31 cm. [ A 1.2 ]
1.3 a triangle with base 30 m and
height 5,5 m. [ A 1.3 ]
1.4 a parallelogram with length 18 mm
and height 8 mm. [ A 1.4 ]
1.5 an isosceles triangle with base
38 cm and height 18 cm. [ A 1.5 ]
1.6 an equlateral triangle with side
56 m and height 46,4 m. [ A 1.6 ]
1.7 a circle with radius 23,4 cm. [ A 1.7 ]
1.8 a circle with diameter 4,65 m. [ A 1.8 ]
Bereken die volume en oppervlakte van elk
van die volgende reëlmatige liggame:
2.1 'n reghoekige prisma met lengte 0,85 m,
breedte 21 cm en hoogte 185 mm.
[ A 2.1 ]
2.2 'n kubus met sye = 67 cm. [ A 2.2 ]
2.3 'n prisma, 34 cm lank en met 'n
reghoekige driehoek waarvan die
reghoeksye 15 cm en 18 cm
lank is, as basis. [ A 2.3 ]
van die volgende reëlmatige liggame:
2.1 'n reghoekige prisma met lengte 0,85 m,
breedte 21 cm en hoogte 185 mm.
[ A 2.1 ]
2.2 'n kubus met sye = 67 cm. [ A 2.2 ]
2.3 'n prisma, 34 cm lank en met 'n
reghoekige driehoek waarvan die
reghoeksye 15 cm en 18 cm
lank is, as basis. [ A 2.3 ]
Calculate the volume and surface area of each
each of the following regular bodies:
2.1 a rectangular prism wih length 0,85 m,
breadth 21 cm and height 185 mm.
[ A 2.1 ]
2.2 a cube with sides 67 cm long. [ A 2.2 ]
2.3 a prism, 34 cm long and having as
base a right-angled triangle with
right-angled sides 15 cm
and 18 cm long. [ A 2.3 ]
each of the following regular bodies:
2.1 a rectangular prism wih length 0,85 m,
breadth 21 cm and height 185 mm.
[ A 2.1 ]
2.2 a cube with sides 67 cm long. [ A 2.2 ]
2.3 a prism, 34 cm long and having as
base a right-angled triangle with
right-angled sides 15 cm
and 18 cm long. [ A 2.3 ]
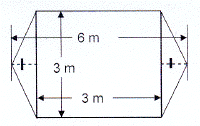
Bereken die oppervlakte van elke figuur in die
diagramme en die omtrek van figure 3.2, 3.4
en 3.5.
3.1
[ A 3.1 ]
3.3
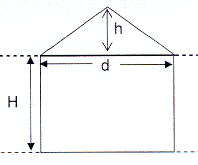
H = 14 m ; d = 20 m ; h = 5,5 m
[ A 3.3 ]
3.5
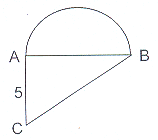
∠DAC = 90° ; BC = 13
[ A 3.5 ]
diagramme en die omtrek van figure 3.2, 3.4
en 3.5.
3.1

[ A 3.1 ]
3.3

H = 14 m ; d = 20 m ; h = 5,5 m
[ A 3.3 ]
3.5

∠DAC = 90° ; BC = 13
[ A 3.5 ]
Calculate the area of every figure in the
diagrams and the perimeter of the figures
in 3.2, 3.4 and 3.5.
3.2
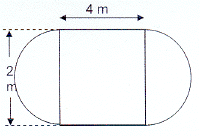
[ A 3.2 ]
3.4
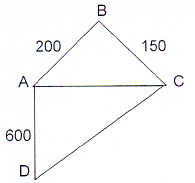
Albei driehoeke ABC en ADC is
reghoekige driehoeke met ∠ABC en
∠DAC die regte hoeke.
Both triangles ABC and ADC are
right-angled triangles with ∠ABC and
∠DAC the right-angles.
[ A 3.4 ]
diagrams and the perimeter of the figures
in 3.2, 3.4 and 3.5.
3.2

[ A 3.2 ]
3.4

Albei driehoeke ABC en ADC is
reghoekige driehoeke met ∠ABC en
∠DAC die regte hoeke.
Both triangles ABC and ADC are
right-angled triangles with ∠ABC and
∠DAC the right-angles.
[ A 3.4 ]
'n Groentetonnel bestaan uit 'n metaalraam in
die vorm van 'n halwe silinder wat met plastiek
oortrek is. Die deursnit van die halwe sirekel
is 15 m en die twee halwe sirkels
is 20 m van mekaar.
4.1 Hoe groot is die oppervlakte van
die grond wat in die tonnel is? [ A 4.1 ]
4.2 Kan die hele oppervlakte gebruik word
om groente te plant? Verduidelik.
[ A 4.2 ]
4.3 Bereken die volume lug in die tonnel.
[ A 4.3 ]
die vorm van 'n halwe silinder wat met plastiek
oortrek is. Die deursnit van die halwe sirekel
is 15 m en die twee halwe sirkels
is 20 m van mekaar.
4.1 Hoe groot is die oppervlakte van
die grond wat in die tonnel is? [ A 4.1 ]
4.2 Kan die hele oppervlakte gebruik word
om groente te plant? Verduidelik.
[ A 4.2 ]
4.3 Bereken die volume lug in die tonnel.
[ A 4.3 ]
A greenhouse consists of a metal frame in the
form of a cylinder with half circles at the
ends and covered with plastic. The diameter
of each semi-circles is 15 m and they
are 20 m apart.
4.1 What area of ground is covered by
the greenhouse? [ A 4.1 ]
4.2 Can all the ground be used to plant
vegetables? Explain.
[ A 4.2 ]
4.3 Calculate the volume of the air in
the greenhouse. [ A 4.3 ]
form of a cylinder with half circles at the
ends and covered with plastic. The diameter
of each semi-circles is 15 m and they
are 20 m apart.
4.1 What area of ground is covered by
the greenhouse? [ A 4.1 ]
4.2 Can all the ground be used to plant
vegetables? Explain.
[ A 4.2 ]
4.3 Calculate the volume of the air in
the greenhouse. [ A 4.3 ]
Jy vervaardig tenks in die vorm van of
'n reghoekige prisma, of 'n kubus of
'n silinder. Elke tenk het 'n kapasiteit van
5 000 liter. Die reghoekige prisma se lengte
is driemaal sy breedte. Elke tenk, behalwe die
kubus, het 'n hoogte van 2 m.
5.1 Bereken die volume van elke soort
tenk in kubieke meter, m3 [ A 5.1 ]
5.2 Bereken die afmetings van elke tenk.
[ A 5.2 ]
'n reghoekige prisma, of 'n kubus of
'n silinder. Elke tenk het 'n kapasiteit van
5 000 liter. Die reghoekige prisma se lengte
is driemaal sy breedte. Elke tenk, behalwe die
kubus, het 'n hoogte van 2 m.
5.1 Bereken die volume van elke soort
tenk in kubieke meter, m3 [ A 5.1 ]
5.2 Bereken die afmetings van elke tenk.
[ A 5.2 ]
You manufacture tanks in the shape of
a rectangle, a cube and a cylinder.
Each tank has a capacity of 5 000 litre.
The rectangular prism's length is thrice its
breadth. Each tank, except the cube, has
a height of 2 m.
5.1 Calculate the volume of each kind of
tank in cubic metres, m3, [ A 5.1 ]
5.2 Calculate the dimensions of each tank.
[ A 5.2 ]
a rectangle, a cube and a cylinder.
Each tank has a capacity of 5 000 litre.
The rectangular prism's length is thrice its
breadth. Each tank, except the cube, has
a height of 2 m.
5.1 Calculate the volume of each kind of
tank in cubic metres, m3, [ A 5.1 ]
5.2 Calculate the dimensions of each tank.
[ A 5.2 ]
Jack moet blikke met Pilchards in
Tomato sauce, blikke met Tuna in Water
en blikke met Tuna in Oil op 'n rak in die
winkel pak sodat elke soort vis dieselfde
oppervlakte beslaan.
Die rak is 1,65 m lank en 25 cm breed.
Die hoogte tussen rakke is 23 cm.
Die blik met Pilchards het 'n deursnit
van 7,5 cm en 'n hoogte van 110 mm.
Die blikke met Tuna het 'n radius van
43 mm en 'n hoogte van 37 mm.
Hoeveel blikke van elke soort vis
kan hy op die rak pak?
[ A 6. ]
Tomato sauce, blikke met Tuna in Water
en blikke met Tuna in Oil op 'n rak in die
winkel pak sodat elke soort vis dieselfde
oppervlakte beslaan.
Die rak is 1,65 m lank en 25 cm breed.
Die hoogte tussen rakke is 23 cm.
Die blik met Pilchards het 'n deursnit
van 7,5 cm en 'n hoogte van 110 mm.
Die blikke met Tuna het 'n radius van
43 mm en 'n hoogte van 37 mm.
Hoeveel blikke van elke soort vis
kan hy op die rak pak?
[ A 6. ]
Jack has to shelve tins of Pilchards in .
Tomato sauce, tins of Tuna in Water and
tins of Tuna in Oil so that each kind if fish
occupies the same area on the shelf.
The shelf is 1,65 m long and 25 cm wide.
The height between two consecutive shelves
is 23 cm. The tin with Pilchards has a
diameter of 7,5 cm and a height of 110 mm.
The tins of Tuna has a radius of 43 mm and
a height od 37 mm. How many tins of each
kind of fish can he put on the shelf?;
[ A 6. ]
Tomato sauce, tins of Tuna in Water and
tins of Tuna in Oil so that each kind if fish
occupies the same area on the shelf.
The shelf is 1,65 m long and 25 cm wide.
The height between two consecutive shelves
is 23 cm. The tin with Pilchards has a
diameter of 7,5 cm and a height of 110 mm.
The tins of Tuna has a radius of 43 mm and
a height od 37 mm. How many tins of each
kind of fish can he put on the shelf?;
[ A 6. ]
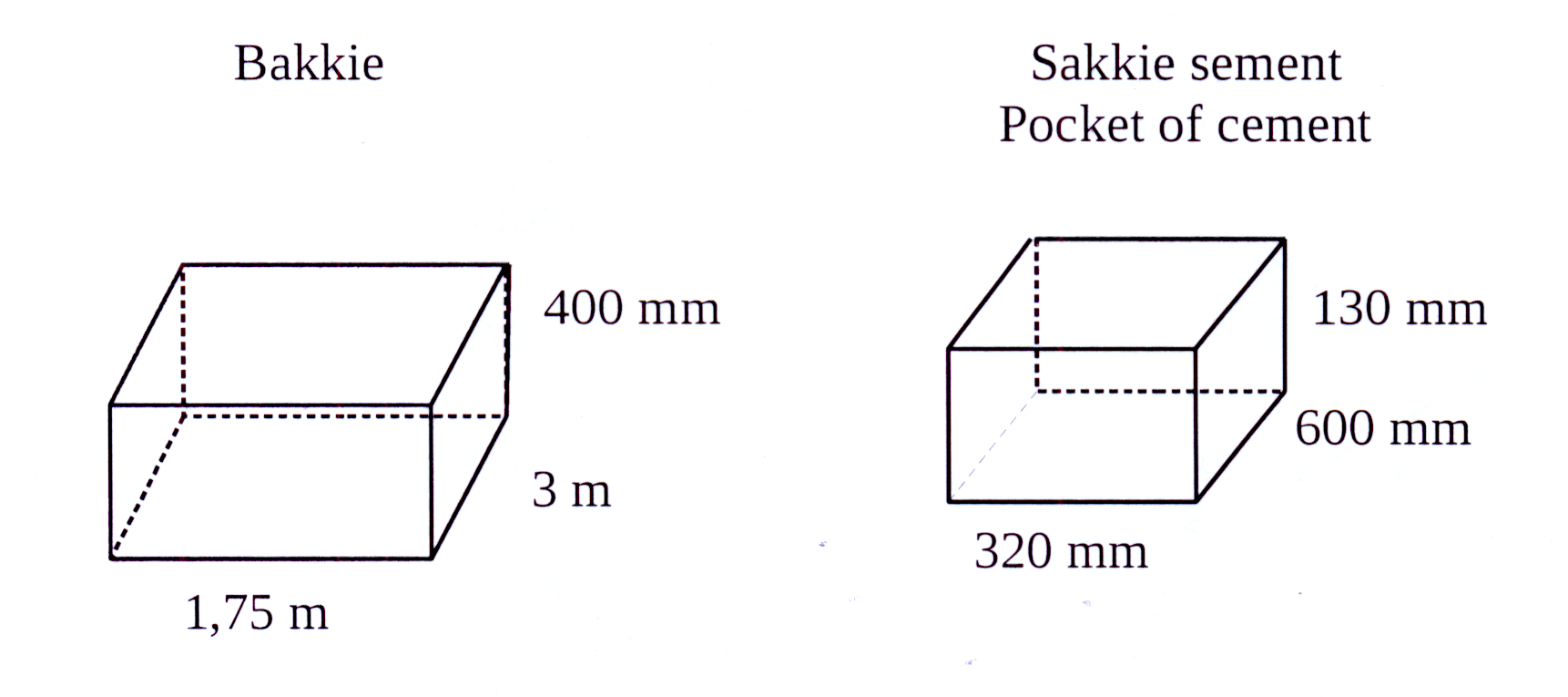
John moet sakkies sement op 'n bakkie laai.
Die bakkie se bak is 3 m lank, 1,75 m wyd en
400 mm diep. Die bakkie kan 2 000 kg dra.
Die afmetings van die sement sakkie is
600 mm lank, 320 mm wyd en 130 mm hoog.
7.1 John pak die sakkies sodat die lengte van
die sakkie ewewydig is aan die lengte van
die bakkie. Hoeveel sakkies kan hy so pak?
[ A 7.1 ]
7.2 John pak die sakkies sodat die breedte van
die sakkie ewewydig is aan die breedte van
die bakkie. Hoeveel sakkies kan hy so pak?
[ A 7.2 ]
7.3 Wat is die aantal sakkies wat hy in
die laag kan pak? [ A 7.3 ]
7.4 John pak nou die sakkies sodat die
wydte van die sakkie ewewydig is aan
die lengte van die bakkie en die lengte
van die sakkie ewewydig is aan die wydte
van die bakkie. Hoeveel sakkies kan hy
nou in een laag pak?
[ A 7.4 ]
7.5 Hoeveel lae kan John op die bakkie pak
en wat is die maksimum aantal sakkies
wat hy tot op die hoogte van die bakkie
kan pak? [ A 7.5 ]
7.6 Kan die bakkie daardie vrag dra? Bevestig
jou antwoord met 'n geskikte berekening.
[ A 7.6 ]
Die bakkie se bak is 3 m lank, 1,75 m wyd en
400 mm diep. Die bakkie kan 2 000 kg dra.
Die afmetings van die sement sakkie is
600 mm lank, 320 mm wyd en 130 mm hoog.
7.1 John pak die sakkies sodat die lengte van
die sakkie ewewydig is aan die lengte van
die bakkie. Hoeveel sakkies kan hy so pak?
[ A 7.1 ]
7.2 John pak die sakkies sodat die breedte van
die sakkie ewewydig is aan die breedte van
die bakkie. Hoeveel sakkies kan hy so pak?
[ A 7.2 ]
7.3 Wat is die aantal sakkies wat hy in
die laag kan pak? [ A 7.3 ]
7.4 John pak nou die sakkies sodat die
wydte van die sakkie ewewydig is aan
die lengte van die bakkie en die lengte
van die sakkie ewewydig is aan die wydte
van die bakkie. Hoeveel sakkies kan hy
nou in een laag pak?
[ A 7.4 ]
7.5 Hoeveel lae kan John op die bakkie pak
en wat is die maksimum aantal sakkies
wat hy tot op die hoogte van die bakkie
kan pak? [ A 7.5 ]
7.6 Kan die bakkie daardie vrag dra? Bevestig
jou antwoord met 'n geskikte berekening.
[ A 7.6 ]
John has to load pockets of cement on a light
delivery truck.The length of the tray of the
truck is 3 m, it is 1,75 m broad and 400 mm
deep. The truck's maximum load is 2 000 kg.
The dimensions of the cement pocket is :
length = 600 mm, width =320 mm and
height = 130 mm.
7.1 John places the pockets with the length of
the pocket parallel to the truck's length.
How many pockets can he place in a row?
[ A 7.1 ]
7.2 John now places the breadth of the pockets
parallel to the truck's breadth. How many
pockets can place in this row?
[ A 7.2 ]
7.3 How many pockets can he place in
one layer? [ A 7.3 ]
7.4 John now places the pockets so that
their breadths are parallel to the truck's
length and their lenghts are parallel to
the truck's breadth. How many pockets
can he now place in one layer?
[ A 7.4 ]
7.5 How many layers can John place on the
truck and what is the maximum number
of pockets that he can place on the truck
to that height? [ A 7.5 ]
7.6 Can the truck carry that load? Verify your
answer with a suitable calculation.
[ A 7.6 ]
delivery truck.The length of the tray of the
truck is 3 m, it is 1,75 m broad and 400 mm
deep. The truck's maximum load is 2 000 kg.
The dimensions of the cement pocket is :
length = 600 mm, width =320 mm and
height = 130 mm.
7.1 John places the pockets with the length of
the pocket parallel to the truck's length.
How many pockets can he place in a row?
[ A 7.1 ]
7.2 John now places the breadth of the pockets
parallel to the truck's breadth. How many
pockets can place in this row?
[ A 7.2 ]
7.3 How many pockets can he place in
one layer? [ A 7.3 ]
7.4 John now places the pockets so that
their breadths are parallel to the truck's
length and their lenghts are parallel to
the truck's breadth. How many pockets
can he now place in one layer?
[ A 7.4 ]
7.5 How many layers can John place on the
truck and what is the maximum number
of pockets that he can place on the truck
to that height? [ A 7.5 ]
7.6 Can the truck carry that load? Verify your
answer with a suitable calculation.
[ A 7.6 ]