Grade 11 - More Exercises.
Financial Documents, tariffs, accounts - Answers
1.1.1
tariff: 0 - 6 kl - gratis and 7 - 18 kl - R2 / kl
1.1.2
Amount = R(6 x 0 + (18-6) x 2) + VAT = R(0 + 24) + (14% of R24)
= R24 + 3,36 = R27,36
1.2
38,12 kl rounded up to 39 kl.
Amount = R(6 x 0 + (19-6) x 2 + (39 - 19) x 2,40) + VAT
= R(0 + 26 + 48) + (0,14 x 74) = R74,00 + 10,36 = R84,36
1.3
Amount = R(6x0 + (19-6)x2 + (39-19)x2,40 + (59-39)x3,50 + (75-59)x4,50) + VAT
= R(0 + 26 + 48 + 70 + 72) + (0,14 x 216) = R(216 + 30,24) = R246,24
There is a mistake. The correct amount, VAT included, is R246,24
2.1
John's total expenses = R17 550 which is greater than his income and thus he can not afford
all his expenses.
2.2
Not yet - his expenses are still R350 more than his income. He can spend R200 less on
clothes and R150 less on entertainment.
2.3
His expenses exceed his income by R650. He can save R350 on clothes and R300 on
entertainment to balance his budget.
3.1
Complete the following table :
| |
| Consumption (kl) |
0 |
10 |
20 |
21 |
30 |
40 |
| Cost (R) |
0 |
10 |
20 |
22 |
40 |
60 |
|
3.2
See accompanying graph.
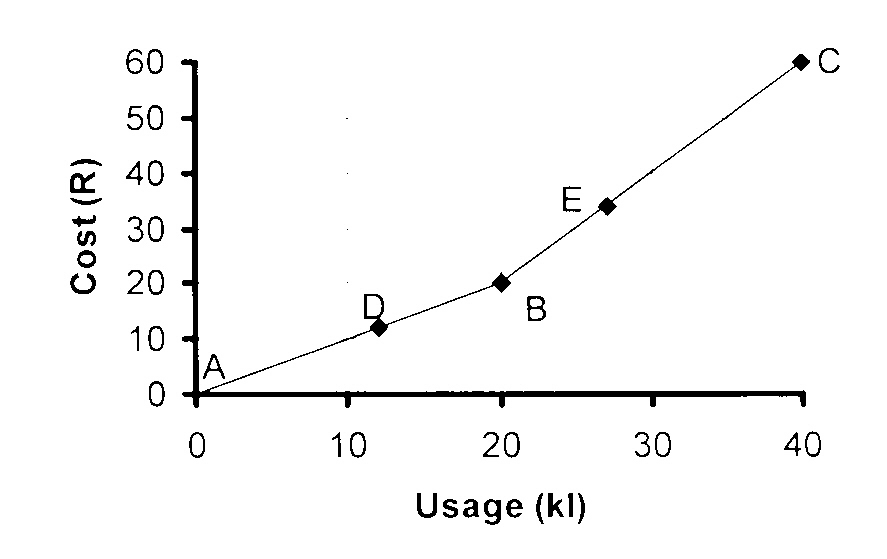
3.3
Minimum cost = R22.00
3.4
Maximum cost = R20.00
3.5
The graph has an upward slope - it has a
positive gradient and the cost increases
as the consumption increases.
The cost is directly proportional to the
consumption.
3.6
D is the point (12 ; 12)
3.7
E is the point (27 ; 35)
3.8
Consumption = 12 kl : Cost = R12 x 1 = R12
4.1
If the consumption = 12 kl the cost = R12.00 and if cost = R76 the consumption = 33 kl
4.2
Maximum cost for consu,ption of 30 kl is R40
4.3
Minimum cost for consumption of 10 kl is R10
R20
4.4
From A to B the cost per kl = ——— = R1
20 kl
R40
From B to C the cost per kl = ——— = R2
20 kl
R76
4.5
At D the cost for 12 kl = R12 x 1 = R12.00 and at E the consumption = ——— = 38 kl
R2/kl
5.1
The graph of contract B starts in the origin, the point (0 ; 0), because there is no cost if
no phone calls are made.
5.2
The graph of contract A starts at the point (0 ; 100) because there is a fixed cost of R100
and the fixed cost does not depend on calls that are made, i.e. the total cost is R100 plus
the cost of the calls that are made.
5.3
Contract B has the greater cost per minute because the graph has the greater gradient / the
graph has the greater slope / the graph is the steeper of the two.
5.4
Contract A has the cost = R147.00 and contract B has the cost = R95.00
5.5
For contract B the time = 115 minutes.
5.6
The graphs intersect in the point (200; 225). It means that the cost is the same for both
contracts if the time = 200 minutes.
5.7
For contract A the cost of the calls = R250 - R100 = R150
R150
For contract A the cost per minute = —————— = R0,60
250 minutes
R275
For contract B the cost per minute = —————— = R1,10
250 minutes
5.8
For contract A the cost = R(100 + 80 x 0,60 = R148
For contract B the cost = R80 x 1,10 = R88
R121
For contract B the time = ———— = 110 minutes
R1,10
5.9
After 200 minutes
5.10
Contract B because the cost for 150 minutes or less is lower.
6.1
Part AB represents the part where the cost remains constant on R100, regardless of
the duration of the calls, provided that it does not exceed 100 minutes.
6.2
Part BC represents the part where the cost increases as the time increases - the cost
is directly proportional to the duration of the call.
6.3
Yes, because the cost increases if the time increases.
6.4
Q is the cheaper contract because the cost remains R100 for any total duration less than 100.
6.5
P is the cheaper cantract because the cost is lower than that of contract Q.
6.6
P has the lower rate per minute because the gradient / slope of the graph is the
smaller / the line is not so steep as the other.
7.1
Phone number is 001 968 0001
7.2
P.O. Box 34, Waterloo. 061208
7.3
Date : 30/04/2015
7.4
Mnr. J Williams
7.5
That amount has been received and payed into the account so that there is no longer
any amount due.
7.6
Volume of water = 53 kl
7.7
Cost = R(6 x 0 + 23 x 1,10 + 20 x 1,70 + 4 x 4,50) = R77,30
VAT = R(77,30 x 0,14) = R10,82 ; Total amount = R(77,30 + 10,82) = R88,12
The cost for the water is correct but the VAT is probably wrong because
the Total amount is wrong.
7.8
Consumption = 11236 - 10524 = 712 units ; Cost = R(712 x 1,45) = 1032,40
VAT = R(1032,40 x 0,14) = R144,54 ; Total amount = R(1032,40 + 144,54) = R1 176,94
7.9
Amount = R1 223,30
7.10
Annual levy = R327,60 and the Amount due = R1 722,16
3 931.20
100
7.10
Percentage = ———— X ——— % = 0,425%
925 000
1
8.1
Date : 2 May 2008 and invoice number : 121
8.2
The account is overdrawn - Mr. S. Stephens owes the bank money - he "borrows" money.
8.3
These amounts are withdrawn from the account to pay other accounts.
8.4
Balance = R4802.92- + 11,200.00 = R6397.09
8.5
Balance (04:06) = R1,541.34 + R3,380.54- = R1,839.20-
OR Balance (04:06) = R1,541.34 − R3,380.54 = R1,839.20-
More money is withdrawn than that is available and therefore the Balance is negative to
show this.
8.6
Credits are positive because they represent money that is paid into the account.
8.7
Balance (04:18) = R3,966.20− + R1,500.00 = R2,466.20−
8.8
Balance (04:30) = R4,270.32− + R99.00− = R4,369.32−
13.5
8.9
Interest on overdrawn account = R4,369.32 x ———— x 1 = R49.15
100 x 12
8.10
Balance (04:30) = R4,369.32− + R49.15− = R4,418.47−
9.1
Overtime 1.5 rate = R85 x 1,5 = R127.50 so that
wages = R127.50 x 10 = R1,275.00
9.2
Overtime 2 rate = R85 x = R170.00 so that
765.00
Number of hours = ———— = 4,5
170.00
9.3
Total wages = R13,200.00 + 1,275.00 + 765.00 = R15,240.00
9.4
Taxable income for the year = R15,240.00 x 12 = R182,880.00
Tax = R21,960 + 25% of (182,880 − 122,000) = R21,960 + 15,220 = R37,180
Tax payable = R37,180 − 8,280 (primary rebate) = R28,900
Monthly payment = R2,408.33
1
9.5
Contribution to UIF = R13,200.00 x ——— = R152.40
100
198
100
9.6
Percentage = ———— X —— = 1,5%
13200
1
9.7
Total deductions = R2,408.33 + 152.40 + 198.00 + 85.25 + 500.00 + 1,518.88
= R5,025.86
9.7
Net wages = R(15,240.00 − 5,025.86) = R10,214.14
