Grade 12 - More exercises.
Straight line graphs.

1.
The accompanying
diagram shows the
graph of the
distance travelled by
by each of
two cars, A and B.
1.1
Describe the
motion of car A
for the first 2 hours, i.e. from t = 0 to t = 2
1.2
What
happens at point P?
1.3
At what speed
does car A travel
for the first 2 hours?
1.4
Which car
travels at the higher speed
from t = 0 to t = 2? Explain.
1.5
At what
average speed does car A travel from t = 0 to t = 3 hours? Explain.
1.6
At what
average speed does car B travel from t = 0 to t = 3 hours?
1.7
Is there a
a time when the cars travel at the same speed? Explain.
1.8
Both
cars travel at the same average speed for the journey, i.e. from t = 0 to t = 6 hours.
Do you
agree? Explain.
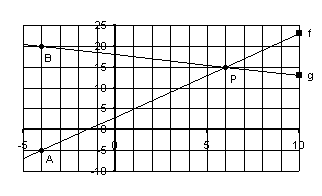
2.
The accompanying
diagram shows the graph
of f: y = 2x + 3 .
2.1
Calculate
the value of y if x = –2 and x = 8.
2.2
Calculate the
value of x if y = 4 and if y = –5
g is
a second line defined by y = 18 – 0,5x
2.3
Calculate the
value of y on g if x = –2 and if x = 8.
2.4
Calculate the
value of x on g if y = 17 and if y = 13.
2.5
Calculate the
co-ordinates of P, the point of
intersection of f and g.
2.6
Say
which of the following statements is true and give a reason:
If x = –2 then (a) 2x + 3 = 18 – 0,5x OR
(b) 2x + 3 < 18 – 0,5x
OR (c) 2x + 3 > 18 – 0,5x
2.7
Say
which one of the following statements is true and give a reason:
If x = –2 then (a) f = g OR (b) f < g
OR (c) f > g .
2.7
Repeat
2.6 but with x = 8.
2.8
Say for
which value(s) of x will (a) f < g (b) f = g (c) f > g
2.9
M(–2 ; –1)
is a point on f and N(–2 ; 19) is a point on g. Write down the length of line MN.
2.10
Now write down
the value of f – g if x = –2.
2.11
Calculate
the value of f – g if x = 8 ; x = 0,5 and x = –4,5.
2.12
For which value(s)
of x will f = 0 ; f < 0 ; f > 0
2.13
For which value(s)
of x will f.g < 0 OR f.g = 0 OR
f.g > 0
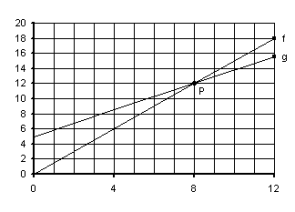
3.
The diagram
shows the graph, f, of the income
realized by selling n items and the
graph, g, of the cost to manufacture the n items.
The graphs
f and g intersect at P.
3.1
Why does
the line f start in the origin (0 ; 0)?
3.2
The
graph of g does not start in the origin.
Explain.
3.3
When is
a profit made? Use the graphs f and g
to answer the question.
3.4
Read
from the graph the income made from the sale of 4 items.
3.5
Show
that the gradient of the line f is 1,5.
3.6
The graph
of f passes through the origin (0 ; 0). Write down the equation of the line f.
3.7
The
equation of line g is y = 0,875x + 5. Show that P, the point of intersection of f and g,
is the
point (8 ; 12).
3.8
Is a
profit made if
3.8.1
8 items are sold?
3.8.2
less than 8 items are sold?
3.8.3
more than 8 items are sold?
3.9
How much
profit is made from the sale of 4 and 10 items?
3.10
The
profit made must be at least R2,5. How many items must be sold?


