Calculate the mean, median, mode and
range of the following data sets :
$$ \hspace*{6 mm}\mathrm{1.1\kern3mm18\ ;\ 24\ ;\ 19\ ;\ 20\ ;\ 28\ ;\ 19\ ;\ 26\ ; } $$
$$ \hspace*{14 mm}\mathrm{21\ ;\ 22\ ;\ 16\ ;\ 17 } $$
$$ \hspace*{6 mm}\mathrm{1.2\kern3mm17\ ;\ 14\ ;\ 11\ ;\ 18\ ;\ 16\ ;\ 17\ ;\ 21\ ; } $$
$$ \hspace*{14 mm}\mathrm{12\ ;\ 22\ ;\ 17 } $$
$$ \hspace*{6 mm}\mathrm{1.3\kern3mm38\ ;\ 60\ ;\ 63\ ;\ 57\ ;\ 60\ ;\ 58\ ;\ 59 } $$
$$ \hspace*{6 mm}\mathrm{1.4\kern3mm50\ ;\ 52\ ;\ 58\ ;\ 51\ ;\ 49\ ;\ 51\ ;\ 80\ ; } $$
$$ \hspace*{14 mm}\mathrm{53\ ;\ 50 } $$
$$ \hspace*{6 mm}\mathrm{1.5\kern3mm50\ ;\ 14\ ;\ 38\ ;\ 23\ ;\ 18\ ;\ 27\ ;\ 30 } $$
$$ \hspace*{6 mm}\mathrm{1.6\kern3mm19\ ;\ 13\ ;\ 23\ ;\ 19\ ;\ 21\ ;\ 19\ ;\ 19 } $$
$$ \hspace*{6 mm}\mathrm{1.7\kern5mm4\ ;\ 17\ ;\ 15\ ;\ 11\ ;\ 25\ ;\ 15\ ;\ 7\ ; } $$
$$ \hspace*{14 mm}\mathrm{15\ ;\ 11\ ;\ 8 } $$
$$ \hspace*{6 mm}\mathrm{1.8\kern3mm37\ ;\ 31\ ;\ 33\ ;\ 34\ ;\ 32\ ;\ 37\ ; } $$
$$ \hspace*{14 mm}\mathrm{31\ ;\ 30\ ;\ 37 } $$
Say which
of the following values,
mean, median and mode, describe
each of the following
sets of data the
best and give good reasons:
$$ \hspace*{6 mm}\mathrm{2.1\kern3mm36\ ;\ 34\ ;\ 31\ ;\ 34\ ;\ 37\ ;\ 32\ ;\ 34 } $$
$$ \hspace*{6 mm}\mathrm{2.2\kern3mm7\ ;\ 8\ ;\ 31\ ;\ 6\ ;\ 9\ ;\ 7\ ;\ 8 } $$
$$ \hspace*{13 mm}\mathrm{7\ ;\ 6 } $$
$$ \hspace*{6 mm}\mathrm{2.3\kern3mm15\ ;\ 11\ ;\ 3\ ;\ 16\ ;\ 16\ ;\ 15 } $$
$$ \hspace*{6 mm}\mathrm{2.4\kern3mm20\ ;\ 17\ ;\ 20\ ;\ 18\ ;\ 23\ ;\ 20 } $$
$$ \hspace*{6 mm}\mathrm{2.5\kern3mm22\ ;\ 26\ ;\ 22\ ;\ 62\ ;\ 21\ ;\ 25 } $$
$$ \hspace*{14 mm}\mathrm{24\ ;\ 22 } $$
$$ \hspace*{6 mm}\mathrm{2.6\kern3mm51\ ;\ 54\ ;\ 92\ ;\ 52\ ;\ 48\ ;\ 53 } $$
$$ \hspace*{14 mm}\mathrm{57\ ;\ 13 } $$
For each set of data calculate the
median, 1
st, 2
nd and 3
rd quartiles,
the inter quartile width, the 20
th,
25
th,
75
th and 80
th percentiles. Also write
down the boundaries between which
we find the middle 50% of the data
values. Write down the maximum value
for the bottom 25% of the values
$$ \hspace*{6 mm}\mathrm{3.1\kern3mm16\ ;\ 33\ ;\ 38\ ;\kern2mm3\ ;\ 23\ ;\ 35\ ;\kern2mm8\ ; } $$
$$ \hspace*{14 mm}\mathrm{15\ ;\ 37\ ;\ 24\ ;\ 36\ ;\ 37\ ;\ 24\ ;\ 36\ ; } $$
$$ \hspace*{14 mm}\mathrm{21\ ;\ 18\ ;\ 31 } $$
$$ \hspace*{6 mm}\mathrm{3.2\kern3mm48\ ;\ 71\ ;\ 58\ ;\ 49\ ;\ 75\ ;\ 57\ ;\ 96\ ; } $$
$$ \hspace*{14 mm}\mathrm{67\ ;\ 92\ ;\ 51\ ;\ 63\ ;\ 95\ ;\ 72\ ;\ 51 } $$
$$ \hspace*{14 mm}\mathrm{93 } $$
$$ \hspace*{6 mm}\mathrm{3.3\kern3mm\kern2mm9\ ;\ 13\ ;\ 42\ ;\ \kern2mm2\ ;\ 44\ ;\ 15\ ;\ 13\ ; } $$
$$ \hspace*{14 mm}\mathrm{31\ ;\ 18\ ;\ 43\ ;\ \kern2mm3\ ;\ 14\ ;\ 23\ ;\ 16\ ; } $$
$$ \hspace*{14 mm}\mathrm{13\ ;\ \kern2mm4\ ;\ \kern2mm5\ ;\ 12\ ;\ 41\ ;\ \kern2mm7\ ;\ 25 } $$
$$ \hspace*{14 mm}\mathrm{34\ ;\ 11 } $$
$$ \hspace*{6 mm}\mathrm{3.4\kern3mm40\ ;\ 41\ ;\ 31\ ;\ 52\ ;\ 44\ ;\ 32\ ;\ 41\ ; } $$
$$ \hspace*{14 mm}\mathrm{35\ ;\ 49\ ;\ 42\ ;\ 34\ ;\ 37\ ;\ 36\ ;\ 48\ ; } $$
$$ \hspace*{14 mm}\mathrm{41\ ;\ 35 } $$
'n Datastel bestaan uit 5 verskillende
waardes. Die gemiddelde is 23,2 en
die mediaan is 24. Die reikwydte is
10 en die grootste waarde is 28.
4.1
Bereken die kleinste waarde.
4.2
Skryf die waarde van die modus
neer. Verduidelik jou antwoord.
4.3
Hoeveel waardes is kleiner as
die mediaan en hoeveel is
groter as die mediaan? Verduidelik.
4.4
Hoeveel waardes is tussen
die mediaan en die grootste
waarde? Verduidelik.
4.5
Bereken die benaderde som
van al die data waardes.
A set of data consists of 5 different
values. The mean is 23,2 and the
median is 24. The range is 10 and
the greatest value is 28.
4.1
Calculate the smallest value.
4.2
Write down the value of the mode.
Explain your answer.
4.3
How many values are smaller than
the median and how many are
greater than the median? Explain.
4.4
How many values are between
the median and the greatest
value? Explain.
4.5
Calculate the approximate sum
of all the data values.
Die gemiddelde van 7 data waardes is
17,143 en die mediaan is 17.
Die kleinste waarde is 14, sie wydte
is 6 en die modus is 19.
5.1
Bereken die grootste waarde.
5.2
Hoeveel waardes is kleiner
as 17 en hoeveel is groter
as 17? Verduidelik.
5.3
Bereken die benaderde som
5.4
Hoeveel waardes is daar
tussen 14 en 17?
5.5
Hoeveel waardes is tussen
17 en 20? Kan jy hulle
neerskryf? Verduidelik.
The mean of 7 data values is
17,143 and the median is 17.
The smallest value is 14, the range
is 6 and the mode is 19.
5.1
Calculate the greatest value.
5.2
How many values are smaller
than 17 and how many are
greater than 17? Explain.
5.3
Calculate the approximate sum
of the data set.
5.4
How many values are there
between 14 and 17?
5.5
How many values are
between 17 and 20? Can you
write them down? Explain.
'n Datastel bestaan uit 9 heelgetal
waardes. Die kleinste waarde is 7 en
die wydte is 26. Die gemiddelde is 18,
die mediaan is 17 en die modus is 27.
6.1
Skryf die grootste waarde neer.
Ant. 6.1
6.2
Hoeveel waardes is kleiner as
die mediaan en hoeveel is
groter as die mediaan?
Verduidelik.
Ant. 6.2
6.3
Hoeveel waardes is groter as
die gemiddelde? Verduidelik.
Ant. 6.3
6.4
Skryf al die waardes groter
as 16 neer.
Ant. 6.4
6.5
Bereken die benaderde som
van al die waardes.
Ant. 6.5
6.6
Bereken die som van die
waardes in 6.4
Ant. 6.6
6.7
Bereken die som van al die
waardes kleiner as die
mediaan.
Ant. 6.7
A set of data consists of 9 integer
values. The smallest value is 7 and
the range is 26. The mean is 18,
the median is 17 and the mode is 27.
6.1
Write down the largest value.
Ans. 6.1
6.2
How many values are smaller
than the median and how many
are larger than the median?
Explain.
Ans. 6.2
6.3
How many values are larger
than the mean? Explain.
Ans. 6.3
6.4
Write down all the values
greater than 16.
Ans. 6.4
6.5
Calculate the approximate sum
of all the values.
Ans. 6.5
6.6
Calculate the sum of the
values in 6.4
Ans. 6.6
6.7
Calculate the sum of al
the values smaller than the
median.
Ans. 6.7
'n Datastel bestaan uit 10 heeltallige
waardes. Die mediaan is 9, die
modus is 8 (frekwensie van2) en
die gemiddelde is 10,5. Die kleinste.
getal is 2 en die reikwydte is 19.
7.1
Bereken die grootste waarde.
7.2
Hoeveel waardes is kleiner as
en hoeveel is groter as die
mediaan? Verduidelik.
7.3
Sal dit korrek wees om te beweer
dat 50% van die waardes kleiner
is as 9? Verduidelik.
7.4
Hoeveel waardes is groter as die
gemiddelde? Verduidelik.
7.5
Bereken die benaderde som
van al die waardes.
7.6
Hoeveel waardes is kleiner as
die modus? Verduidelik.
A data set contains 10 integer
values. The median is 9, the
mod is 8 (frequency of 2) and
the mean is 10,5. The smallest
number is 2 and the range is 19.
7.1
Calculate the biggest value.
7.2
How many values are smaller
than and how many are larger
than the median? Explain.
7.3
Will it be correct to claim that
50% of the values are smaller
than 9? Explain.
7.4
How many values are greater
than the mean? Explain.
7.5
Calculate the approximate sum
of all the values.
7.6
How many values are smaller
than the mode? Explain.
'n Kolwer behaal 'n gemiddelde van
23,1 lopies in 7 wedstryde. Die lopies
aangeteken in elk van die eerste 6
wedstryde is 21 ; 8 ; 6 ; 88 ; 3 ; 5.
8.1
Hoeveel lopies teken hy in die
sewende wedstryd aan?
8.2
Is die gemiddelde van sy tellings
'n goeie beskrywing van sy tellings?
Verduidelik.
Die tellings van 'n tweede kolwer is :
23 ; 18 ; 20 ; 21 ; 17 ; 19 ; 20
8.3
Bereken die gemiddelde van
sy tellings.
8.4
As jy 'n bestendige kolwer moet
kies, sal jy die eerste of tweede
kolwer kies?? Verduidelik.
A batsman scored an average of
23,1 runs in 7 matches. The runs
scored in each of the first 6 matches
were: 21 ; 8 ; 6 ; 88 ; 3 ; 5
8.1
How many runs did he score in
the seventh match?
8.2
Is the average of his scores a good
description of his scores? Explain.
The scores of a second batsman were:
23 ; 18 ; 20 ; 21 ; 17 ; 19 ; 20
8.3
Calculate the average of his scores.
8.4
If you were to select a steady batsman,
would you choose the first or the
second batsman? Explain.
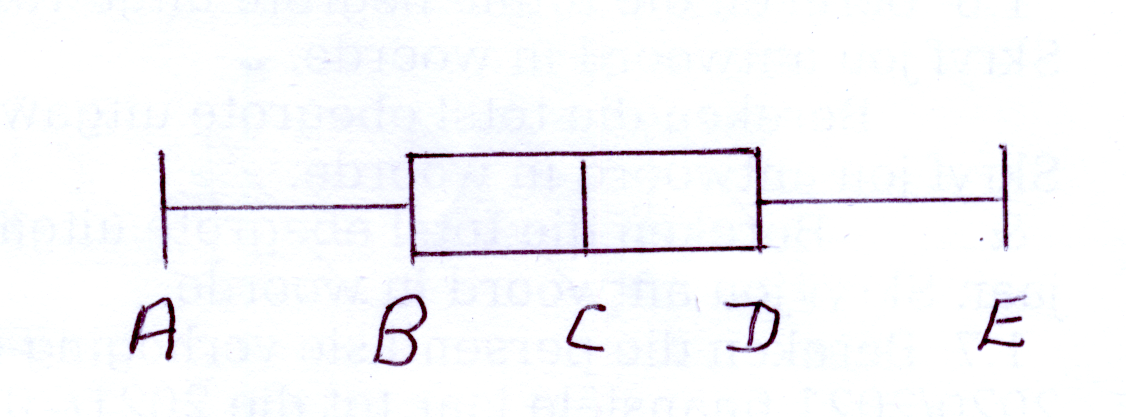
Die diagram hierbo stel die
snor-en-baard diagram van
'n datastel voor sowel as terme
wat die verskillende letters op die
diagram beskryf.
Die terme, nie noodwendig in die
korrekte volgorde nie, :
kwartiel 1, kwartiel 2, kwartiel 3,
maksimum, mediaan, minimum
en modus.
9.1
Gee die korrekte terme vir
die letters op die
snor-baarddiagram deur
slegs die letter en die
korrekte term neer te skryf.
9.2
Voltooi deur die korrekte
letters in te vul :
9.2
Voltooi deur die korrekte
9.2.1
Omvang = __ ━ __
9.2.2
Interkwartielomvang (IKO) = __ ━ __

The diagram above represents
the box-and-whisker diagram of
a set of data as well as terms
that describe the different letters
on the diagram .
The terms, not necessarily in the
correct order, are :
quartile 1, quartile 2, quartile 3,
maximum, median, minimum
and mode.
9.1
Give the correct terms to
identify the letters on the
box-and-whisker diagram
by writing down only the letter
and the correct term.
9.2
Complete by writing down the
letters A to E :
9.2.1
Range = __ ━ __
9.2.2
Interquartile range (IQR) = __ ━ __
'n Datastel het die volgende waardes :
gemiddelde = 25, mediaan = 26,
kleinste waarde = 3, eerste kwartiel = 16,
tweede kwartiel = 26, derde kwartiel = 36
modus = 16 en maksimum waarde = 38.
Verwys na die snor-en-baard diagram van
Vraag 9 en vul dan die korrekte waardes
vir die letters, A tot E, in.
A set of data has the following values :
average = 25, median = 26,
smallest value = 3, first quartile = 16,
second quartile = 26, third quartile = 36,
mode = 16 and maximum value = 38.
Refer to the box-and-whisker diagram in
Question 9 and write down the correct
values for the letters, A to E.
'n Datastel het die volgende waardes :
gemiddelde = 25, mediaan = 26,
kleinste waarde = 3, eerste kwartiel = 16,
tweede kwartiel = 26, derde kwartiel = 36
modus = 16 en maksimum waarde = 38.
Verwys na die snor-en-baard diagram van
Vraag 9 en vul dan die korrekte waardes
vir die letters, A tot E, in.
A set of data has the following values :
average = 25, median = 26,
smallest value = 3, first quartile = 16,
second quartile = 26, third quartile = 36,
mode = 16 and maximum value = 38.
Refer to the box-and-whisker diagram in
Question 9 and write down the correct
values for the letters, A to E.
