1.2 The value of y becomes smaller.
1.3 No. x is indirectly / inversely proportional to y because the product xy is a constant number.
1.4 No. The product, xy is equal to a certain number, which is not 0. There are no real numbers, except 0,
whose product will be equal to 0.
1.5.1 The point (4 ; b) is the point (4 ; 4) and 4 x 4 = 16. The square root of 16 is 4. And thus the coordinates of
the point (4 ; b) represent the square root of 16.
1.5.2 y = x
1.6 m = 0,25 and n = 0,125
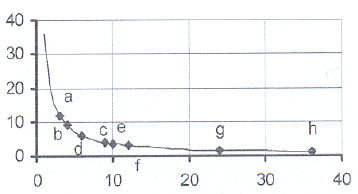2.1 xy = 36 2.2 a = 12 ; b = 4 ; c = 9 ; d = 6
e = 3,6 ; f = 12 ; g = 1,5 ; h = 36
2.3 See the accompanying graph.
2.4 See graph.
2.5 m = 0,25 and n = 180
3.1 xy = 8
3.2 a = 4 ; b = 2 ; c = 1 ; d = 0,25 ; e = 0,125
3.3 M is not on the hyperbola because 0,25 x 16 = 4 and not 8 while N is on the hyperbola because
128 x 0,0625 = 8
4.1 b = 9 and c = 0,5
4.2.1 a = 3
4.2.2 The coordinates of the point (3;a) represent the square root of 9.
5.1 b = 0,5 and c = 1,6
5.2.1 a = 4
5.2.2 The coordinates of the point (a;4) represent the square root of 16.
5.3 Draw the line y = x to intersect the graph of xy = 16. Read the x- or y-coordinate of the point of intersection.
This vakue is equal to the square root of 16.
5.4 Square root (64) = square root (4 x 16)
= square root (4) x square root (16)
= 2 x 4 = 8
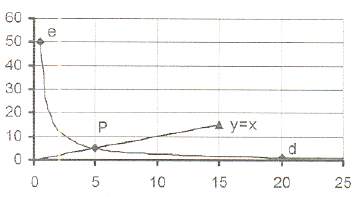6. a = 12,5 ;
b = 6,25 ;
c = 2,5 ; d = 1,25 ; e = 0,5 ; f = 100
6.1 See the graph.
6.2 Square root (100) = square root (4 x 25)
= square root (4) x square root (25)
= 2 x 5 = 10
Square root (1) = square root (100 / 100)
= square root (100) / square root (100)
= 10/10 = 1
6.3.1 y = -40x + 70
6.3.2 Intercept with X-axis is (1,75 ; 0) and
Y-axis is (0 ; 70)
7.1 a = 12 ; b = 3 ; c = 4 ; d = 1,5
7.2 The values of x become bigger.
7.3 No values of x. Suppose y = 0 then xy = x X 0 = 0 which does not satisfy the equation xy = 24.
7.4 Draw the line y = x to intersect the hyperbola xy = 24. The x- or y-coordinate of this point is
the square root of 24.
7.5 Square root (96) = square root (4 X 24)
= square root (4) X square root (24)
= 2 X 4,898979 = 9,798
Square root (6) = square root (24/4)
= square root (24) / square root (4)
= 4,898979 / 2 = 2,449
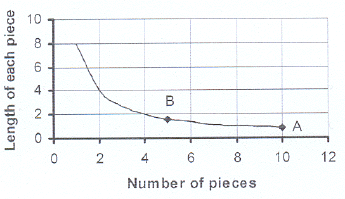8.1 x is inversely proportional to y or y is inversely proportional to x.
xy = 8
8.2 a = 4; b = 4; c = 1
8.3 10 pieces.
8.4 Length = 1, 6 m
8.5.1 The graph is a hyperbola because x is inversely
proportional to y,
8.5.2 See graph.
8.5.3 See graph.
8.5.4 Yes but only so that the length = 8 m. If y becomes
greater than 8, then x must become smaller than 1,
which is not a suitable answer. (The number of pieces are whole numbers).
If the length becomes greater, the number of pieces becomes smaller.
8.5.5 Yes, but not indefinitely. If the number of pieces becomes
greater, the length of a piece becomes smaller.
The length must not be too small.
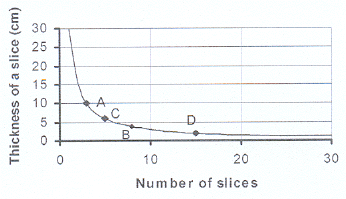9.1 Length of loaf = 300 mm = 30 cm. 9.2 x is inversely proportional to y or y is inversely
proportional to x.
9.3.1 100 mm or 10 cm
9.3.2 37,5 mm or 3,75 cm.
9.4.1 50 slices.
9.4.2 15 slices.
9.5.1 See the graph.
9.5.2 See graph.
9.5.3 See graph.
9.5.4 Yes, but only until the thickness of a
slice = 300 mm, i.e. the length of the loaf. A slice
cannot be thicker than the length of the loaf.
9.5.5 Yes, but not indefinitely. If the number of slices increases,
the thickness of a slice decreases. A slice cannot become too thin.
9.6 300 mm - the length of the loaf.
9.7 About 30 slices. It will depend on the kind of bread. If the slice is too thin, it will crumble.