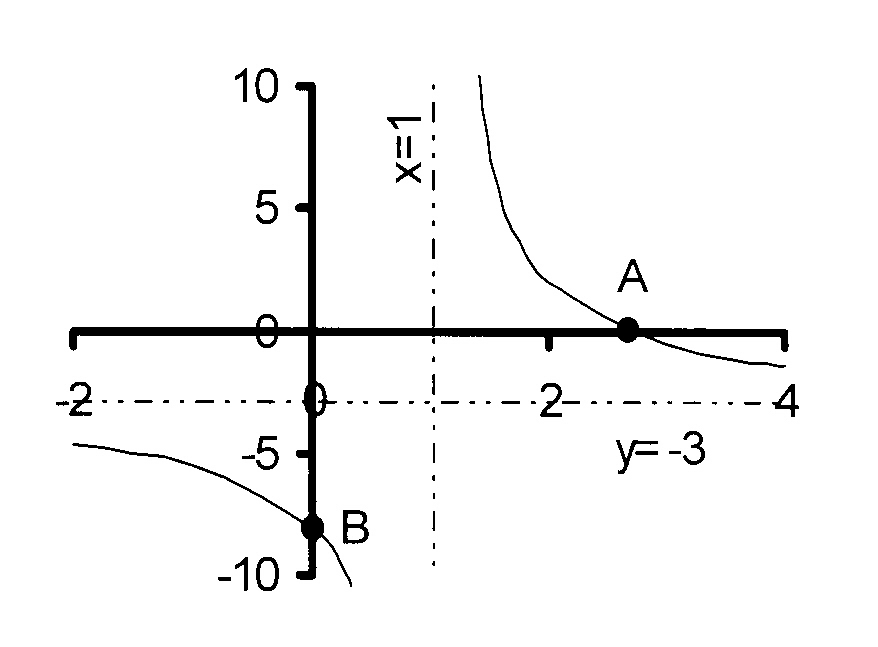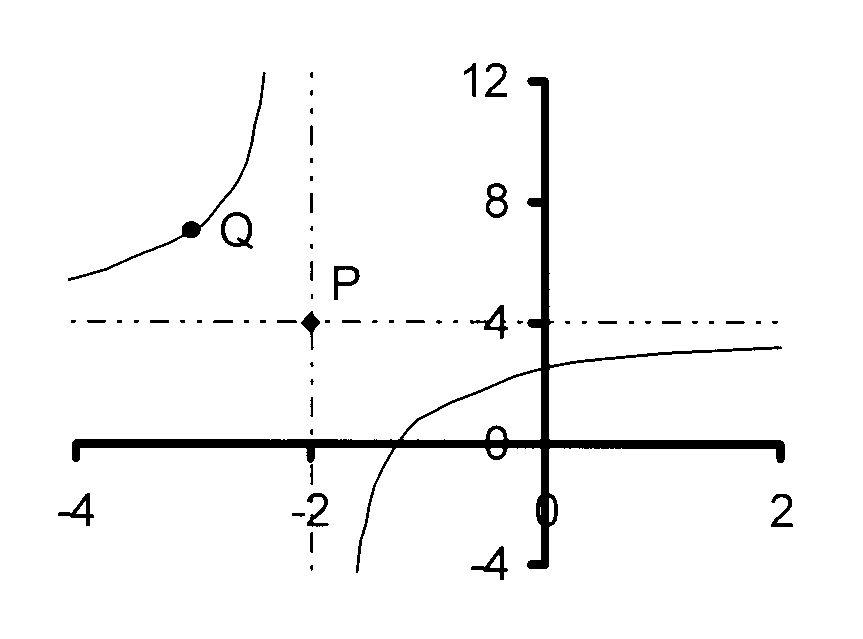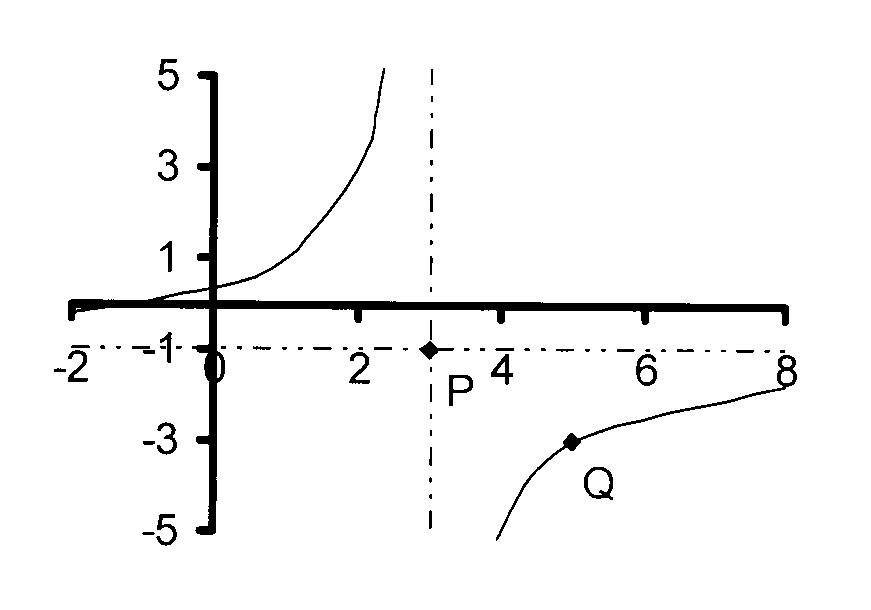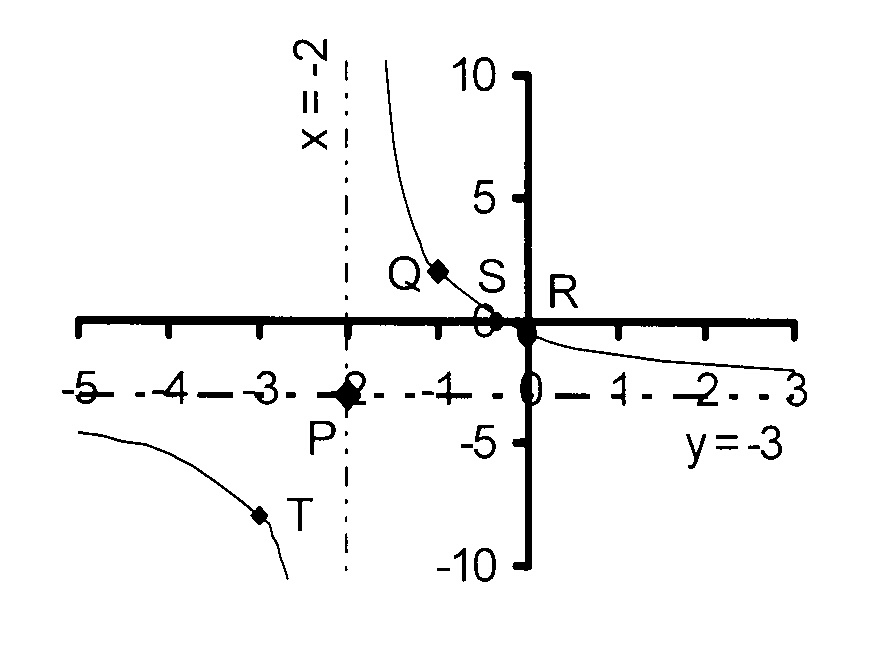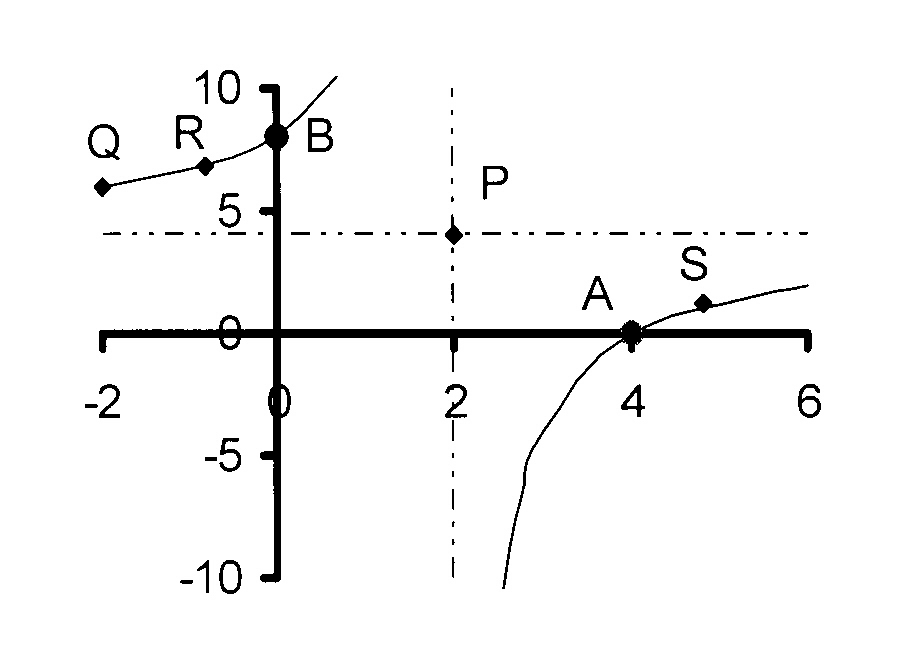Sketch the graphs of the following
functions :
$$ \hspace*{2 mm}\mathrm{1.1\kern3mmy = \frac{2}{x + 1} + 3\kern2mm\ } $$
[ A 1.1 ]
$$ \hspace*{2 mm}\mathrm{1.2\kern3mmy = \frac{3}{x + 2} − 4\kern2mm\ } $$
[ A 1.2 ]
$$ \hspace*{2 mm}\mathrm{1.3\kern3mmy = \frac{5}{x − 3} + 5\kern2mm\ } $$
[ A 1.3 ]
$$ \hspace*{2 mm}\mathrm{1.4\kern3mmy = \frac{−2}{x + 1} + 3\kern2mm\ } $$
[ A 1.4 ]
$$ \hspace*{2 mm}\mathrm{1.5\kern3mmy = \frac{−3}{x − 2} − 4\kern2mm\ } $$
[ A 1.5 ]
$$ \hspace*{2 mm}\mathrm{1.6\kern3mmy = \frac{−5}{x + 3} − 2\kern2mm\ } $$
[ A 1.6 ]
The figures show the graphs of the
$$ \hspace*{5 mm}\mathrm{\kern3mmfunctions\ with\ equation\ y = \frac{a}{x + p}+ q\kern2mm\ } $$
Use the information given in the
figure to detemine the values
of a, p and q :
2.1
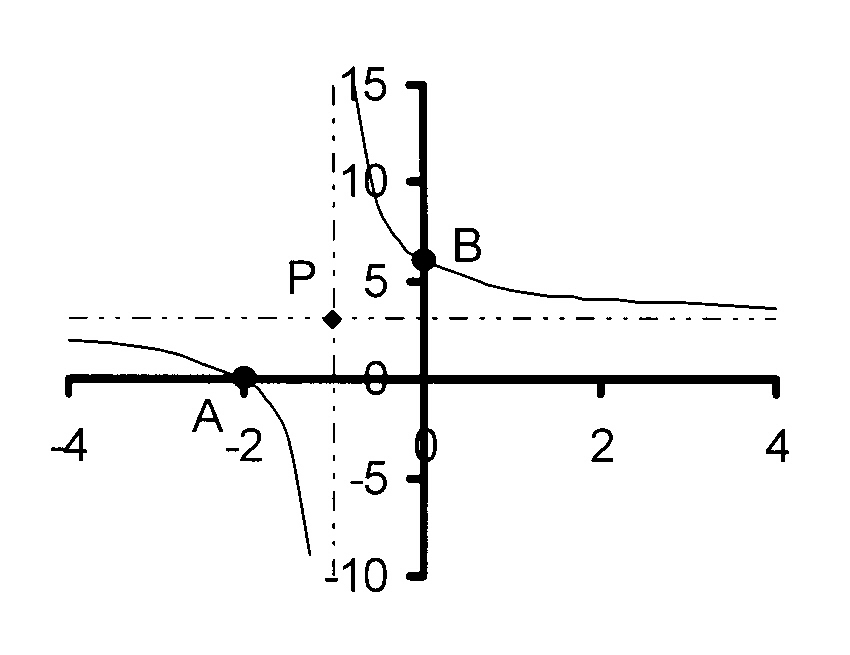
Horizontal asymptote: y = 3 and
vertical symptote: x = - 1
A is the point (−2 ; 0) and
B is the point (0 ; 6)
[ A 2.1 ]
2.2
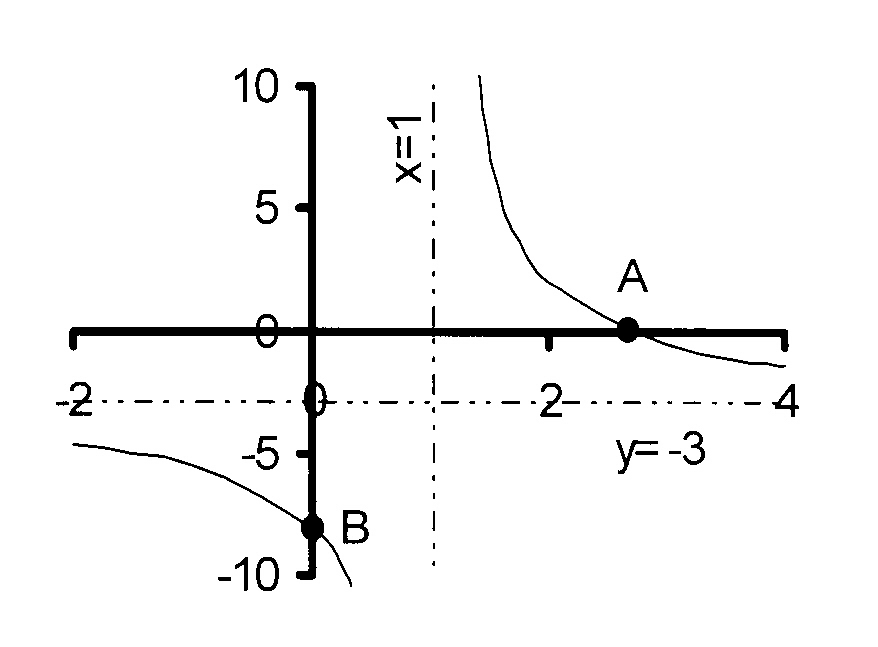
B is the point (0 ; − 8)
[ A 2.2 ]
2.3
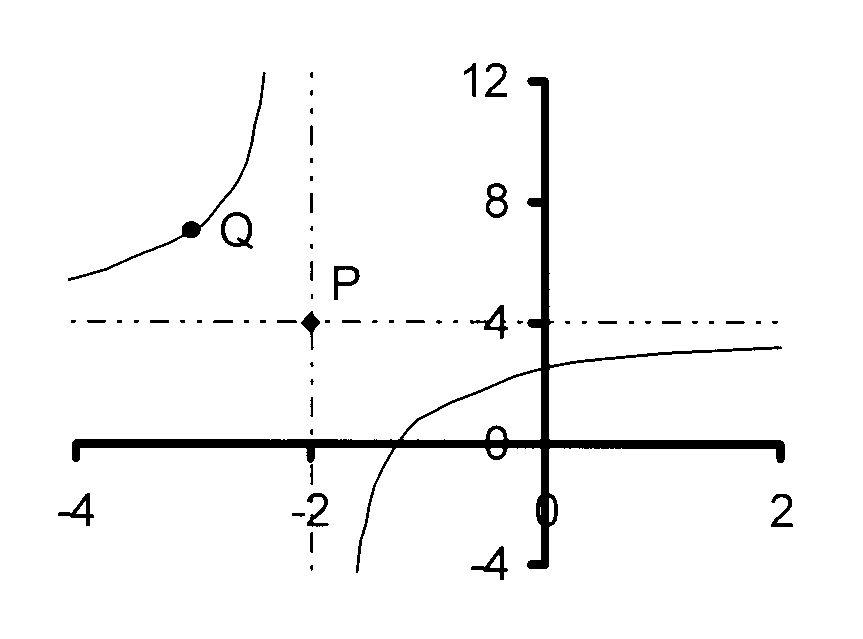
P is the point (-2 ; 4) and
Q(− 3 ; 7)
[ A 2.3 ]
2.4
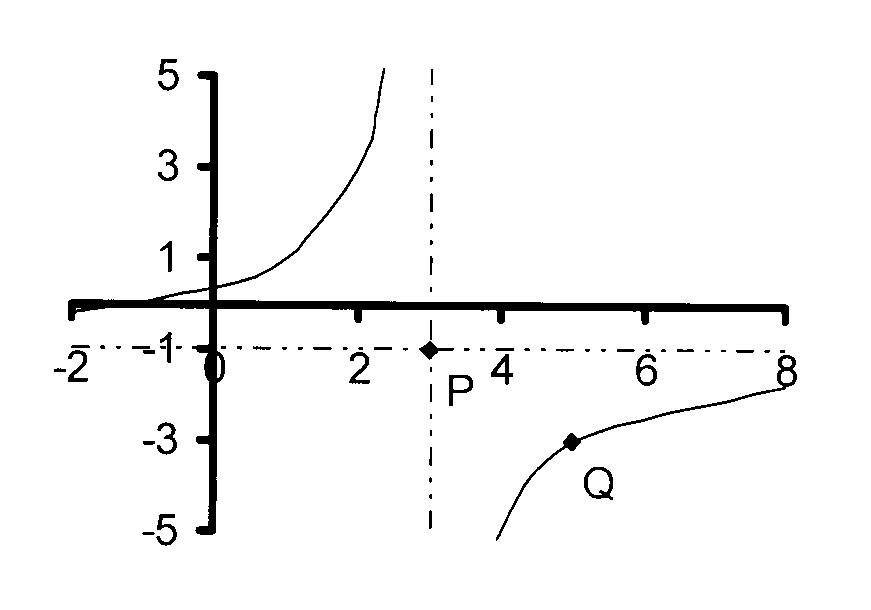
P is the point (3 ; -1) and
Q(5 ; −3)
[ A 2.4 ]
The figure shows the graph of
$$ \hspace*{6 mm}\mathrm{y = \frac{a}{x + p}+ q\kern2mm\ } $$
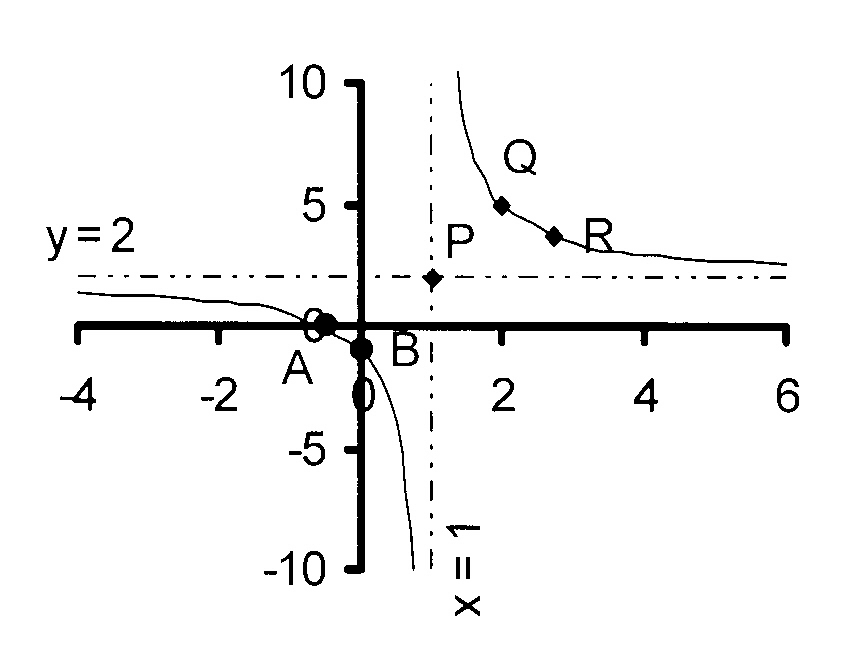
3.1 Write down the coordinates of
point P.
[ A 3.1 ]
3.2 Calculate the values of a, p and
q and write down the equation of
the function given that Q(2 ; 5).
[ A 3.2 ]
3.3 Calculate the coordinates of
points A and B.
[ A 3.3 ]
3.4 Write down the equation for
the positive axis of symmetry.
[ A 3.4 ]
3.5 Calculate the coordinates of R,
the point of intersection of the
hyperbola with the axis of symmetry.
[ A 3.5 ]
The figure shows the graph of
$$ \hspace*{6 mm}\mathrm{y = \frac{a}{x + p}+ q\kern2mm\ } $$
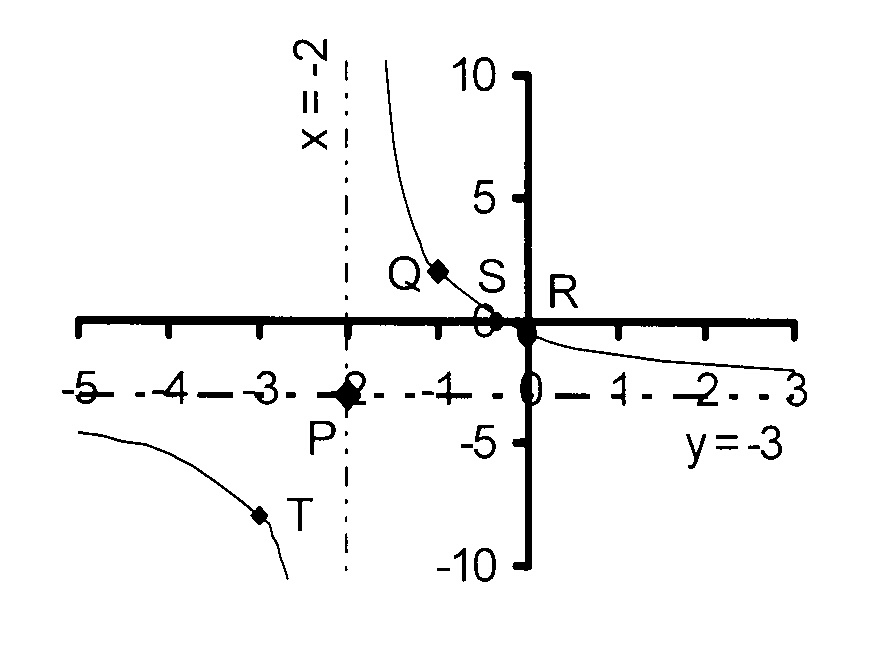
4.1 Write down the coordinates of
point P.
[ A 4.1 ]
4.2 Given that Q is the point (-1 ; 2),
calculate the values of a, p and q and
write down the equation of the function.
[ A 4.2 ]
4.3 Calculate the coordinates of A and B,
the points of intersection with the axes.
[ A 4.3 ]
4.4 Write down the equation for the
positive axis of symmetry.
[ A 4.4 ]
4.5 Calculate the coordinates of T,
the point of intersection of the
hyperbola with the axis of symmetry.
[ A 4.5 ]
4.6 Write down the domain and range
of the graph.
[ A 4.6 ]
The figure shows the graph of
$$ \hspace*{6 mm}\mathrm{y = \frac{a}{x + p}+ q\kern2mm\ } $$
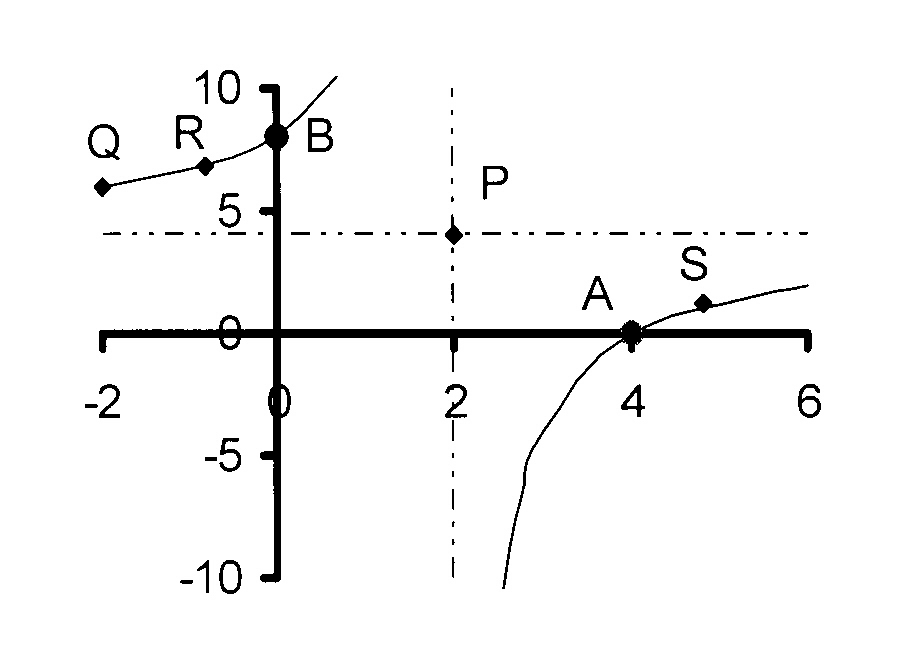
P is the point (2 ; 4)
5.1 Write down the equation of the
horizontal asymptote.
[ A 5.1 ]
5.2 Write down the equation of the
vertical asymptote.
[ A 5.2 ]
5.3 Given that Q is the point (-2 ; 6),
calculate the values of a, p and q
and write down the equation
of the function.
[ A 5.3 ]
5.4 Calculate the coordinates of
points A and B, the intercepts
with the axes.
[ A 5.4 ]
5.5 Write down the equation for the
negative axis of symmetry.
[ A 5.5 ]
5.6 Calculate the coordinates of
R and S, the points of intersection
of the hyperbola with the axis
of symmetry.
[ A 5.6 ]
5.7 Write down the domain and
range of the graph.
[ A 5.7 ]
5.8 h(x) is formed if the graph is
translated 3 units downwards and
5 units to the right. Write down
the equation of h(x) in the form
y =
. . .
[ A 5.8 ]
The figure shows the graph of
$$ \hspace*{10 mm}\mathrm{y = 5 − \frac{6}{x - 3}\kern2mm\ } $$
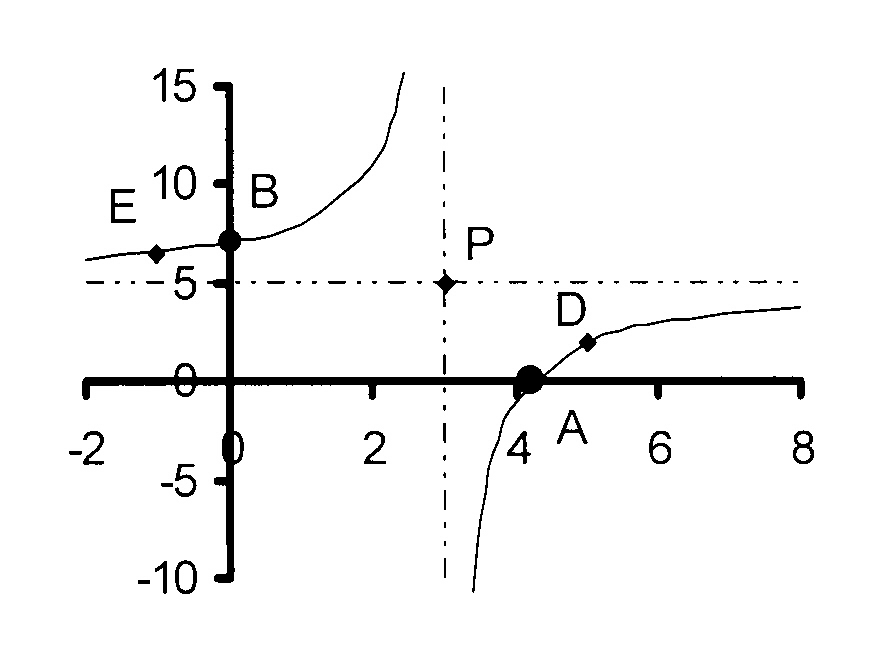
6.1 Write down the equation of the
horizontal asymptote.
[ A 6.1 ]
6.2 Write down the equation of the
vertical asymptote.
[ A 6.2 ]
6.3 Calculate the coordinates of
A, the X-intercept.
[ A 6.3 ]
6.4 Calculate the coordinates of
B, the Y-intercept.
[ A 6.4 ]
6.5 D is the point (5 ; d). Calculate
the value of d.
[ A 6.5 ]
6.6 Calculate the value of e if E is
the point (e ; 6,5).
[ A 6.6 ]
6.7 The line y = − 2x + 15 intersects
the hyperbola at points R and S.
Calculate the coordinates of the
points R and S.
[ A 6.7 ]
The figure shows the graph of
$$ \hspace*{10 mm}\mathrm{y = \frac{− 5}{x + 1} − 3\kern2mm\ } $$
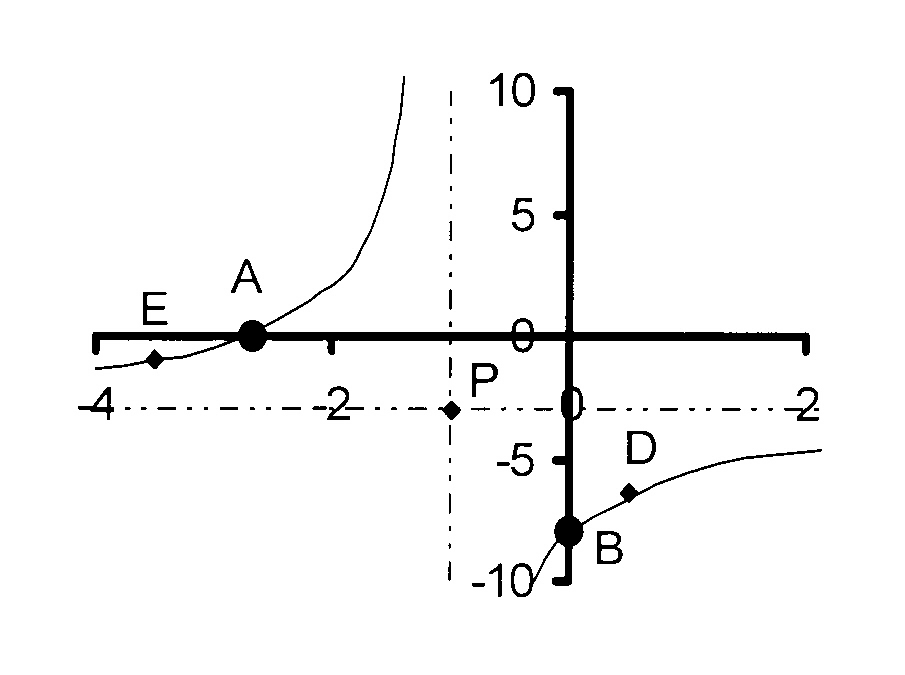
7.1 Write down the coordinates of
P, the point of intersection of
the asymptotes.
[ A 7.1 ]
7.2 Calculate the coordinates of A,
the X-intercept
[ A 7.2 ]
7.3 Calculate the coordinates of B,
the Y-intercept.
[ A 7.3 ]
7.4 D is the point (0,5 ; d). Calculate
the value of d.
[ A 7.4 ]
7.5 Calculate the value of e if E
is the point (e ; − 1).
[ A 7.5 ]
7.6 Write down the equations for
both axes of symmetry.
[ A 7.6 ]
The figure shows the parts p, q, r
and s of two graphs in the form
$$ \hspace*{12 mm}\mathrm{y = \frac{a}{x + p}+ q\kern2mm\ } $$
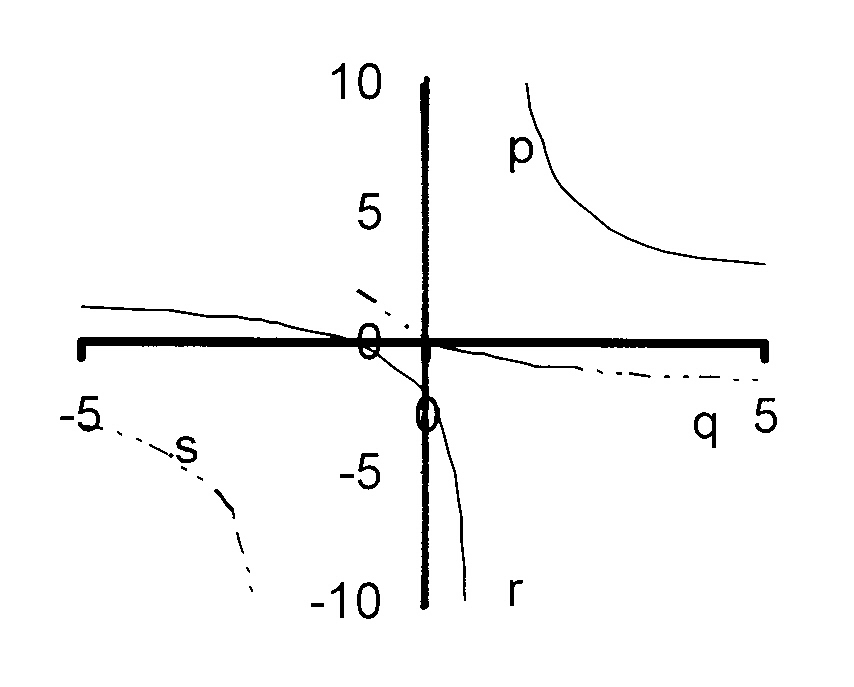
$$ \hspace*{6 mm}\mathrm{One\ graph\ has\ the\ equation\ y = \frac{4}{x − 1} + 2\kern2mm\ } $$
and the other has the equation
$$ \hspace*{12 mm}\mathrm{y = \frac{4}{x + 2} − 2\kern2mm\ } $$
8.1 Say which pieces fit which
graph.
[ A 8.1 ]
8.2 How was one graph translated to
form the other?
[ A 8.2 ]