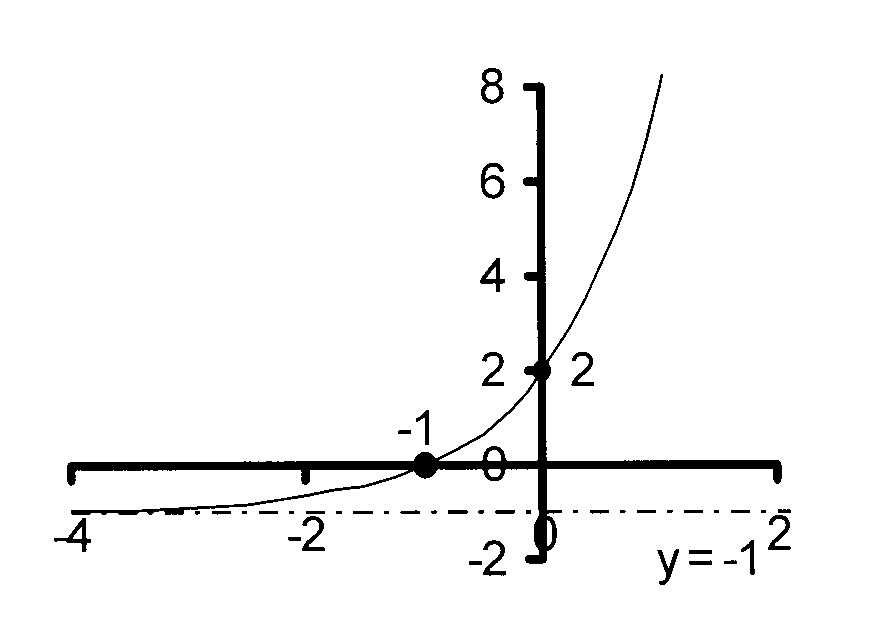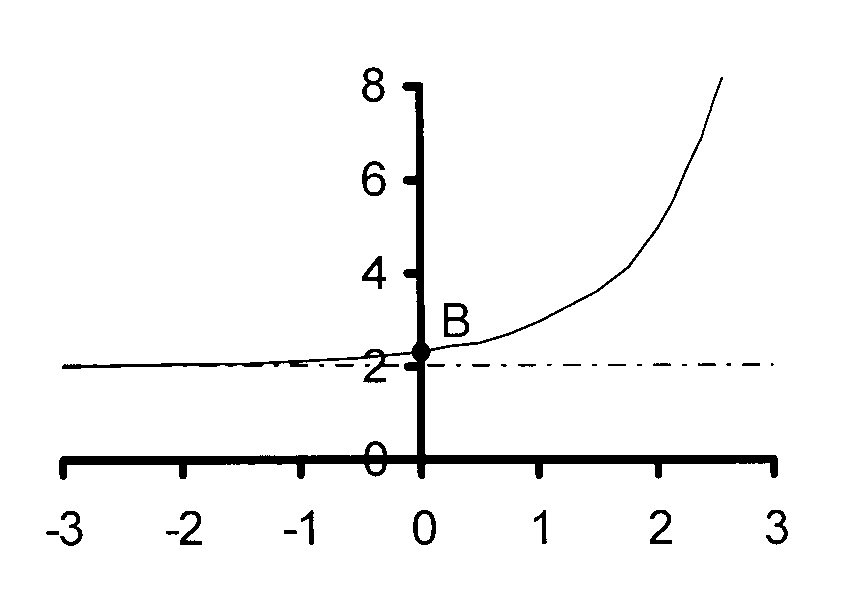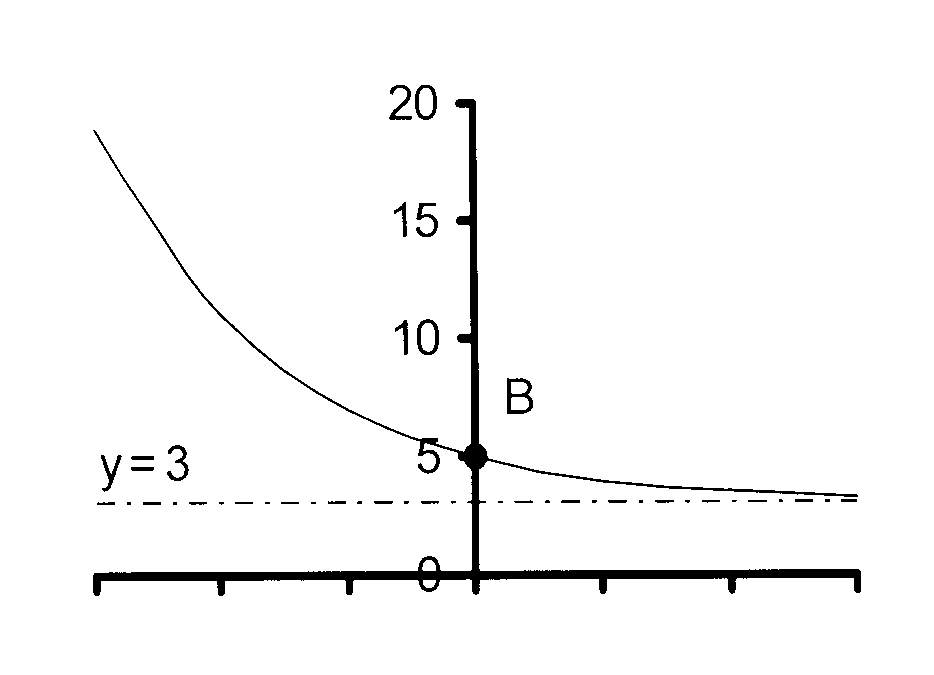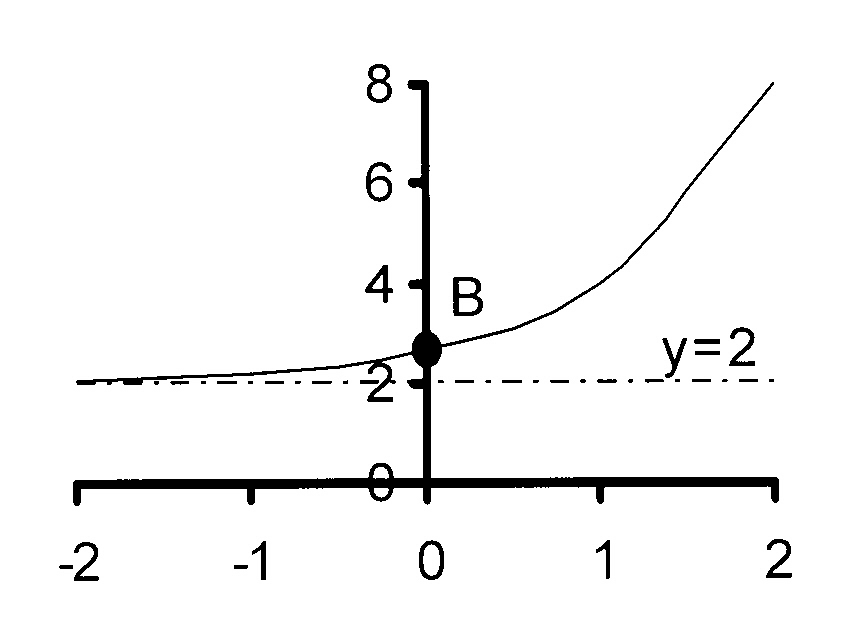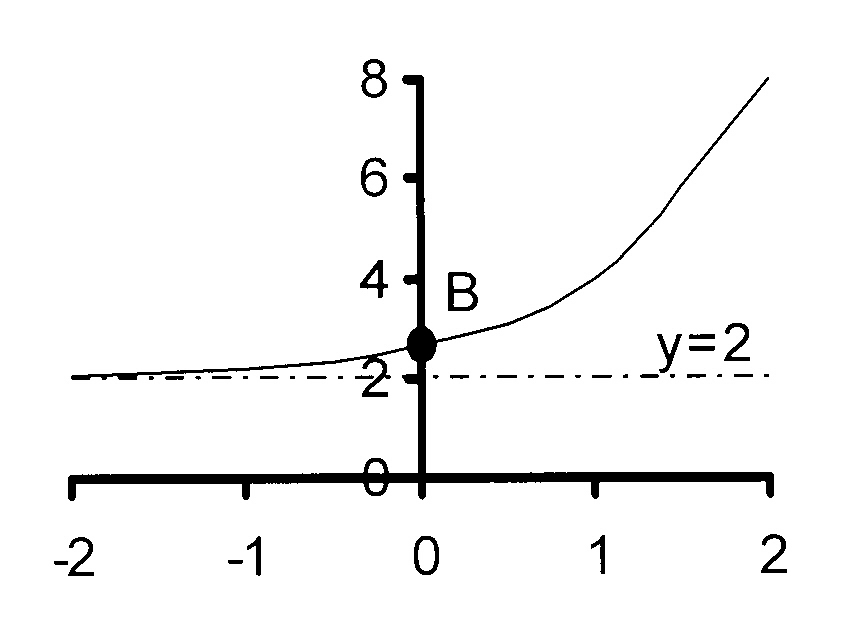Graad 11 Wiskunde - Nog Oefeninge.
Grafieke van die eksponensiŽle funksie : antwoorde.
1.1
y = 3x + 1 − 1
1.2
y = 3x − 1 + 2
Horisontale asimptoot: y = − 1
Horisontale asimptoot: y = 2
Basis > 0, funksie is stygend.
Basis > 0, funksie is stygend.
Y-afsnit: y = 30 + 1 − 1
Y-afsnit: y = 30 − 1 + 2
= 3 − 1
= 3 − 1 + 2
= 2
= 2,333
Y-afsnit is (0 ; 2)
Y-afsnit is (0 ; 2,33)
X-afsnit: 3x + 1 − 1 = 0
Geen X-afsnit nie want q > 0.
3x + 1 = 1 = 30
x + 1 = 0
x = − 1
X-afsnit is (− 1 ; 0)
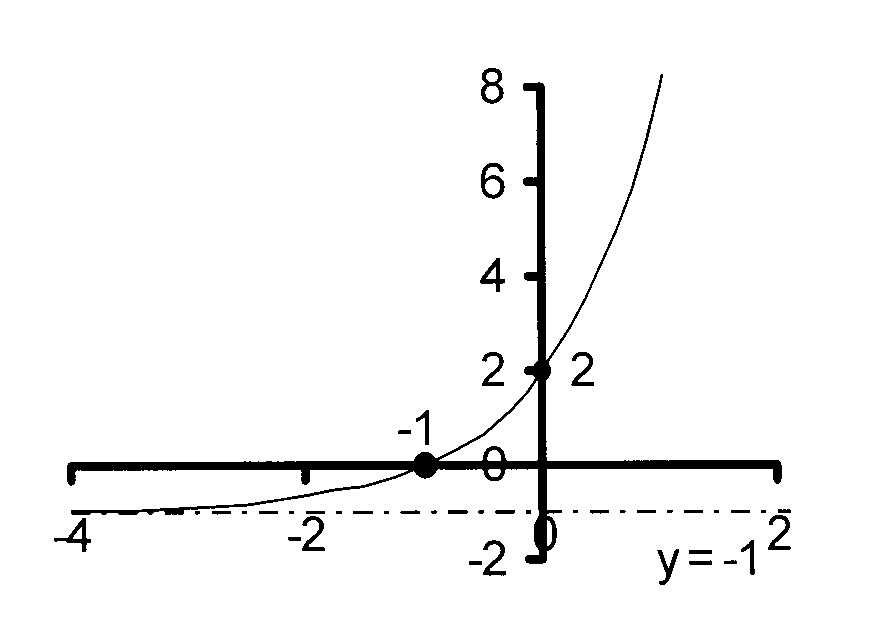
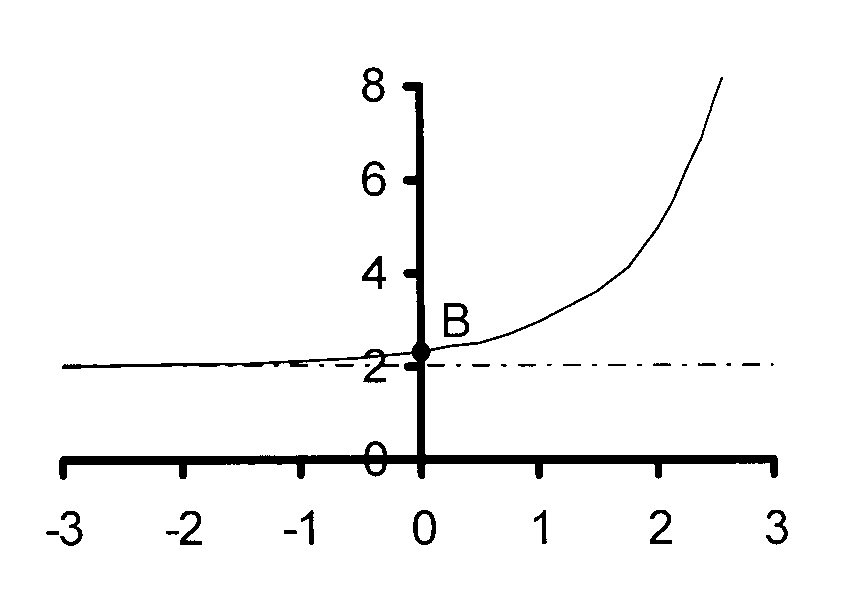
1.3
y = 21 − x + 3
1.4
y = 32 − x − 3
Horisontale asimptoot: y = 3
Horisontale asimptoot: y = − 2
Basis < 0, funksie is dalend.
Basis > 0, funksie is stygend.
Y-afsnit: y = 21 − 0 + 3
Y-afsnit: y = 32 − 0 − 3
= 2 + 3
= 9 − 3
= 5
= 6
Y-afsnit is (0 ; 5)
Y-afsnit is (0 ; 6)
Geen X-afsnit nie want q > 0
X-afsnit: 32 − x − 3 = 0
32 − x = 3
2 − x = 1
x = 1
X-afsnit is (1 ; 0)
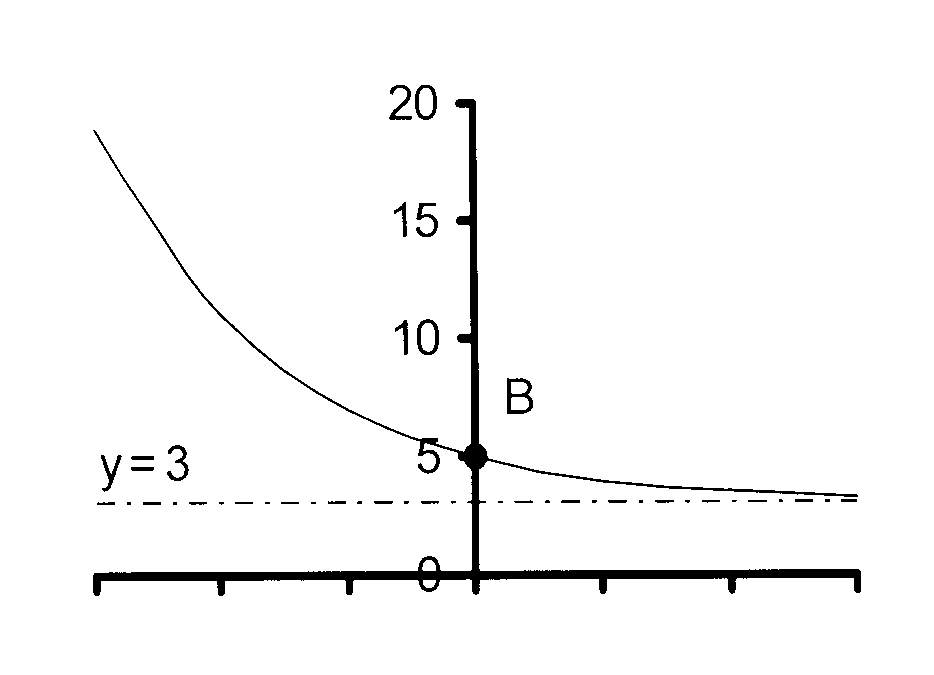
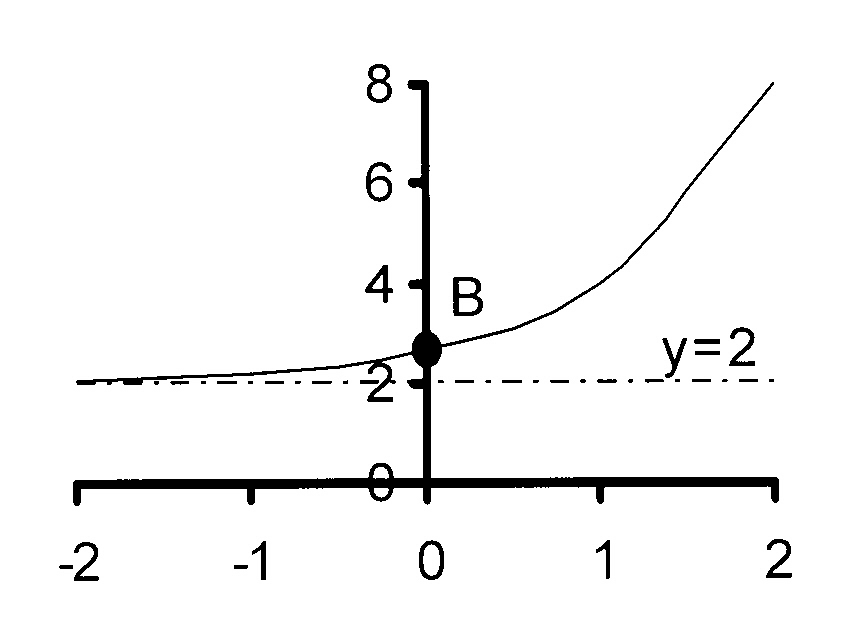
1.5
y = 2.3x − 1 + 2
1.6
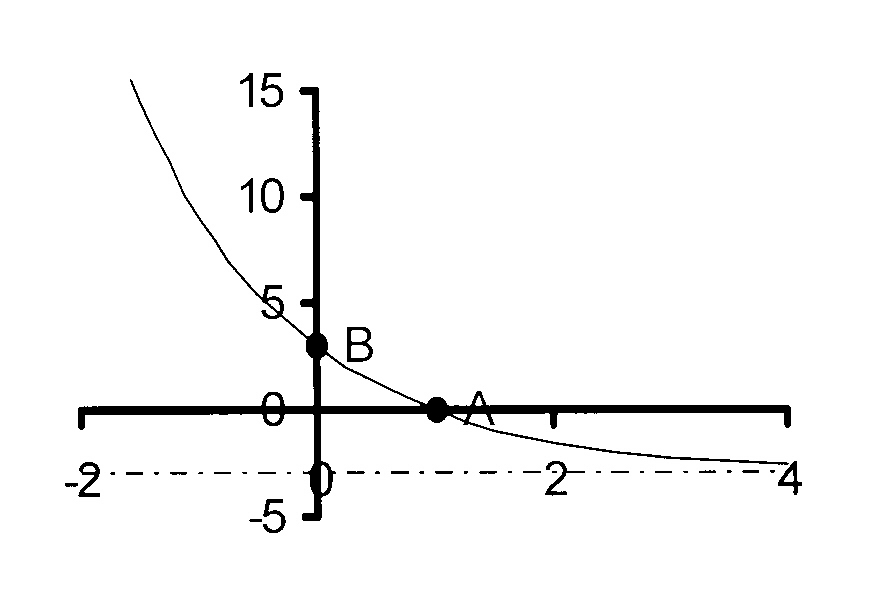
y = 3.21 − x − 3
Horisontale asimptoot: y = 2
Horisontale asimptoot: y = − 3
Basis > 0, funksie is stygend.
Basis < 0, funksie is dalend.
Y-afsnit: y = 2.30 − 1 + 2
Y-afsnit: y = 3.21 − 0 − 3
= 2.3 − 1 + 2
= 3.21 − 3
= 2,667
= 3
Y-afsnit is (0 ; 2,67)
Y-afsnit is (0 ; 3)
Geen X-afsnit nie want q > 0
X-afsnit: 3.21 − x − 3 = 0
3.21 − x = 3
21 − x = 1 = 20
1 − x = 0
x = 1
X-afsnit is (1 ; 0)
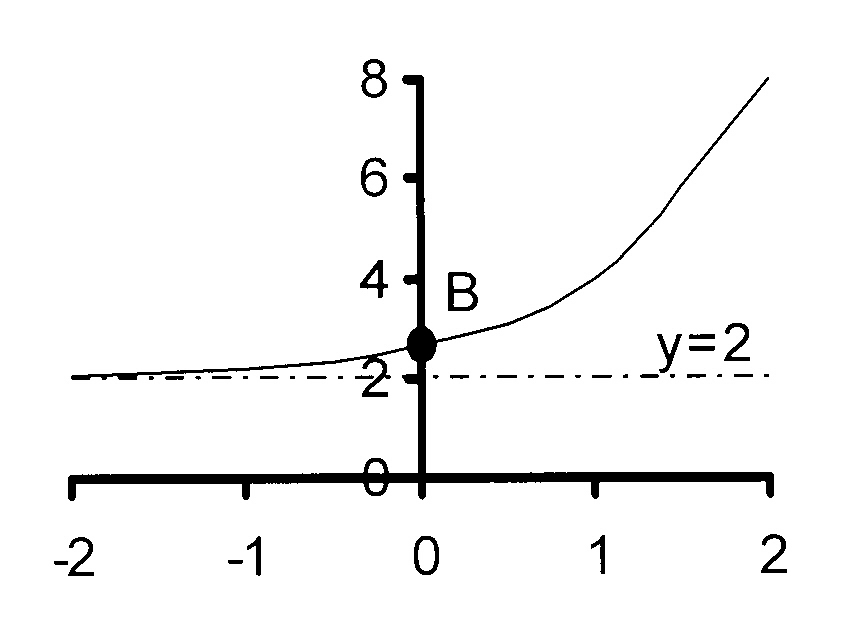
1
2.1
y = 2x + p + q
2.2
y = (——)x + p + q
3
Horisontale asimptoot: y = 1 en dus q = 1
Horisontale asimptoot: y = − 3 en dus q = −3
1
y = 2x + p + 1
y = (——)x + p −3
3
1
By (0 ; 1,5): 20 + p + 1 = 1,5
By (2;−2): (——)2 + p −3 = −2
3
2p = 0,5 = 2−1
3− 2 − p = 1 = 30
p = −1
− 2 − p = 0
p = − 2
1
y = 2x − 1 + 1
y = (——)x − 2 −3
3
1
2.3
y = 2x + p + q
2.4
y = (——)x + p + q
2
Horisontale asimptoot: y = −2 en dus q = −2
Horisontale asimptoot: y = − 2 en dus q = 2
1
y = 2x + p − 2
y = (——)x + p + 2
2
1
By (2 ; −1): 22 + p − 2 = −1
By (1;3): (——)1 + p + 2 = 3
2
1
1
22 + p = 1 = 20
(——)1 + p = 1 = (——)0
2
2
2 + p = 0
1 + p = 0
p = − 2
p = − 1
1
Vergeluking : y = 2x − 2 − 2
Vergelyking : y = (——)x − 1 + 2
2
2.5
y = a.2x + q
2.6
y = a.bx + q
Horisontale asimptoot: y = −1 en dus q = 1
Horisontale asimptoot: y = − 3 en dus q = − 3
y = a.bx + 1
y = a.bx − 3
By (0 ; 3): a.b0 + 1 = 3
By (0;0): ab0 − 3 = 0
a.1 = 2
a − 3 = 0
a = 2
a = 3
y = 2.bx + 1
y = 3.bx − 3
By (1 ; 7): 2.b1 + 1 = 7
By (−2;9): 3.b−2 − 3 = 9
2b = 6
3b−2 = 12
1
b = 3
b = 2−1 = (—)
2
1
Vergelyking : y = 2x − 2 − 2
Vergelyking : y = (——)x − 1 + 2
2
3.1
y = 4x − 1 − 2
4.1
y = 2−x + 1 + 2
Y-afsnit: y = 40 − 1 − 2
Y-afsnit: y = 20 + 1 + 2
= 4− 1 − 2
= 21 + 2
= − 1,75
= 4
Y-afsnit is (0 ; − 1,75)
Y-afsnit is (0 ; 4)
X-afsnit: 4x − 1 − 2 = 0
X-afsnit: Die horisontale asimptoot is groter
4x − 1 = 2 = 40,5
as 0 en daarom is daar nie 'n
x − 1 = 0,5
X-afsnit nie.
x = 1,5
X-afsnit is (1,5 ; 0)
3.2
By P(2 ; p): p = 42 − 1 − 2
4.2
By P(−1 ; p) p = 2−(−1) + 1 + 2
= 41 − 2
= 22 + 2
= 2
= 6
3.3
By R(r ; −1): 4r − 1 − 2 = −1
4.3
By R(r ; 2,25) 2−r + 1 + 2 = 2,25
4r − 1 = 1 = 40
2−r + 1 = 0,25 = 2− 2
r − 1 = 0
−r + 1 = − 2
r = 1
r = 3
3.4
Definisieversameling : {x | x ∈ R}
4.4
Definisieversameling : {x | x ∈ R}
3.5
Waardeversameling : {y | y ≠ − 2; y ∈ R}
4.5
Waardeversameling : {y | y > 2; y ∈ R}
4.6
h(x) = 2−x + 1 + 2 − 4
= 2−x + 1 − 2
1
1
5.1
y = (——) x − 1 − 4
5.2
By C(c;4): (——) c − 1 − 4 = 4
2
2
1
Y-afsnit: y = (——) 0 − 1 − 4
(2 − 1) c − 1 = 8
2
1
= (——) 0 − 1 − 4
2 − c + 1 = 23
2
= 4 − 4 = 0
− c + 1 = 3
1
X-afsnit: (——) x − 1 − 4 = 0
c = − 2
2
(2 − 1) x − 1 = 4
5.3
Definisieversameling : { x | x ∈ R }
2 − x + 1 = 22
5.4
Waardeversameling: { y | y > −4; y ∈ R }
1
− x + 1 = 2
5.5
h(x) = (——) x − 1 − 4 + 2
2
x = − 1
1
= (——) x − 1 − 2
2
1
1
6.1
y = (——)x + p + q
6.2
y = (——)x − 2 − 1
3
3
1
Horisontale asimptoot: y = − 1 en dus q = − 1
By P(p;2): (——) p − 2 − 1 = 2
3
1
1
By (0;8): (——) 0 + p − 1 = 8
(——) p − 2 = 3
3
3
(3 −1) p = 9 = 3 2
(3 −1) p − 2 = 3
−p = 2
−p + 2 = 1
p = − 2
p = 1
p = − 2 en q = − 1
6.3
Definisieversameling: { x | x ∈ R }
1
6.5
h(x) = (——)x − 2 − 1 + 3
6.4
Waardeversameling: { y | y > −1; y ∈ R }
3
6.6
Die grafiek word 3 eenhede opwaarts verplaas en dus
1
= (——)x − 2 + 2
3
word alle punte 3 eenhede opwaart verplaas.
Die Y-afsnit van h(x) sal 8 + 3 = 11 wees.