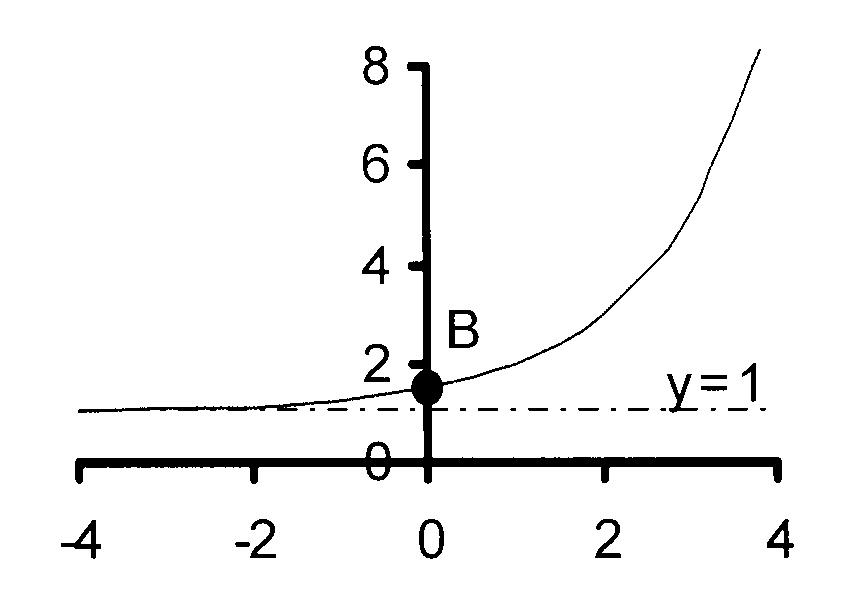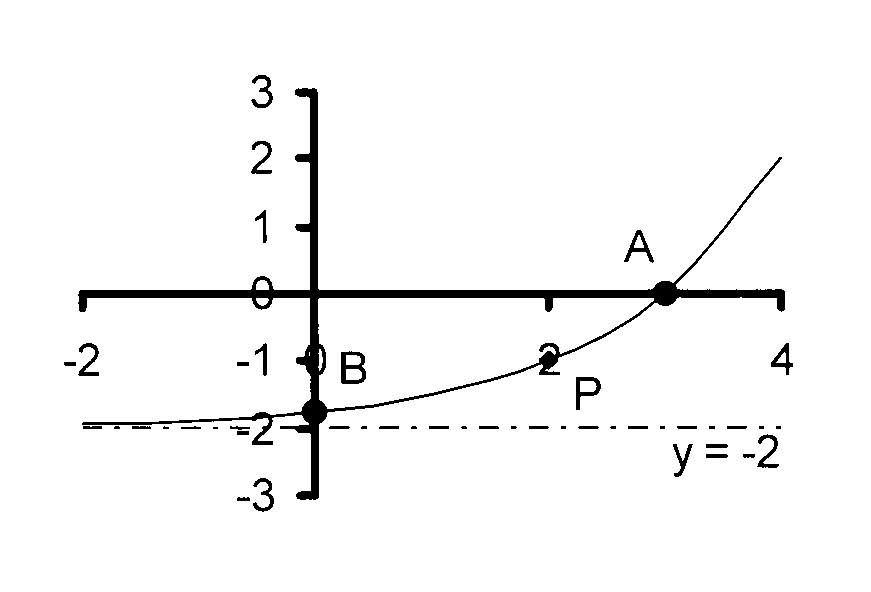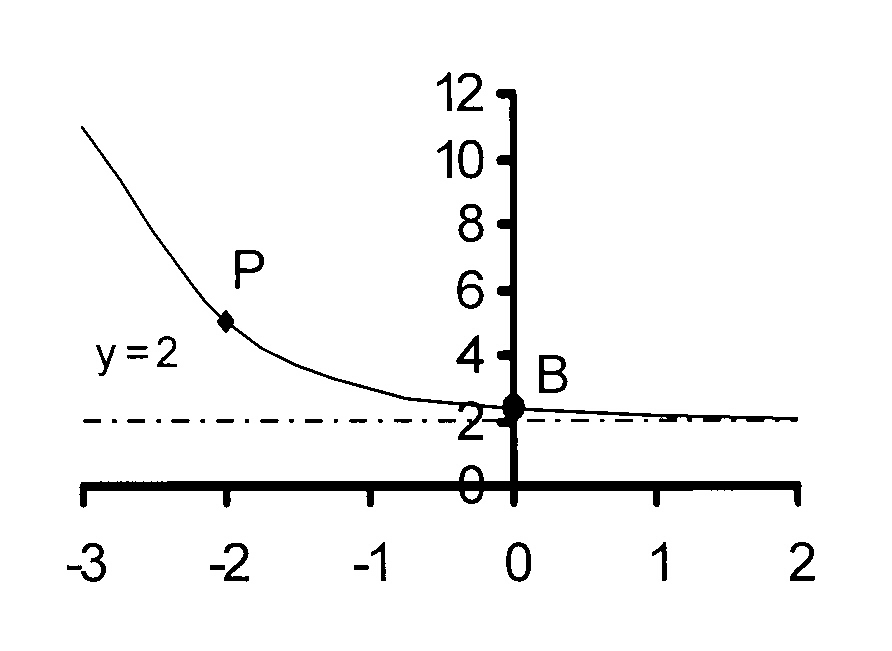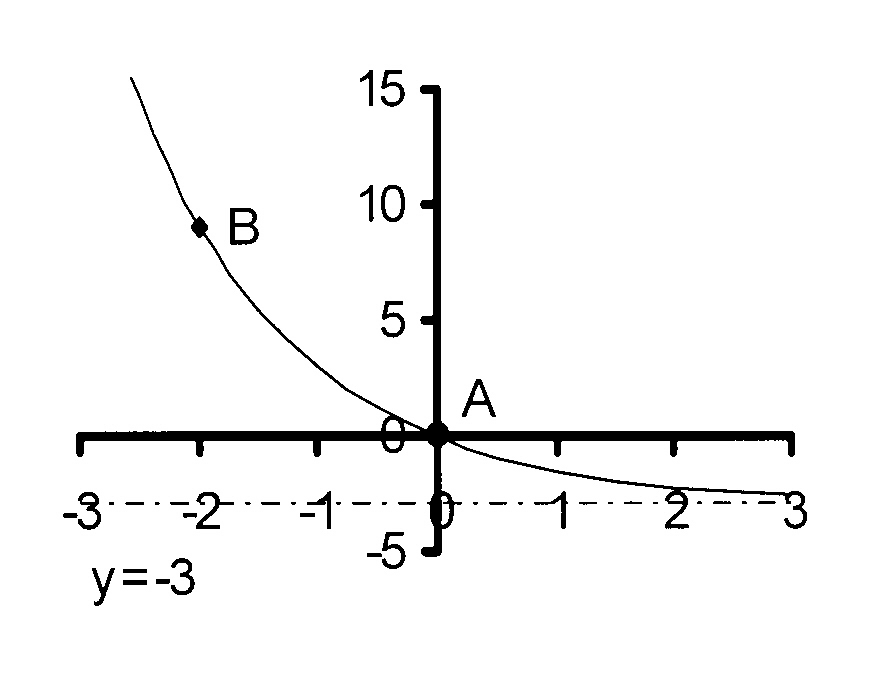Sketch the graphs of the following
functions :
$$ \hspace*{2 mm}\mathrm{1.1\kern3mmy = 3^{x+1} − 1\kern2mm\ } $$
[ A 1.1 ]
$$ \hspace*{2 mm}\mathrm{1.2\kern3mm3^{x − 1} + 2\kern2mm\ } $$
[ A 1.2 ]
$$ \hspace*{2 mm}\mathrm{1.3\kern3mmy = 2^{1 − x} + 3\kern2mm\ } $$
[ A 1.3 ]
$$ \hspace*{2 mm}\mathrm{1.4\kern3mmy = 3^{2 − x} − 3\kern2mm\ } $$
[ A 1.4 ]
$$ \hspace*{2 mm}\mathrm{1.5\kern3mmy = 2.3^{x − 1} + 2\kern2mm\ } $$
[ A 1.5 ]
$$ \hspace*{2 mm}\mathrm{1.6\kern3mmy = 3.2^{1 − x} − 3\kern2mm\ } $$
[ A 1.6 ]
The figures show the graphs of the
$$ \hspace*{3 mm}\mathrm{\kern3mmfunctions\ with\ equation\ y = a^{x + p} + q\kern2mm\ } $$
Use the information given in the figure
to detemine the values of p and q :
2.1
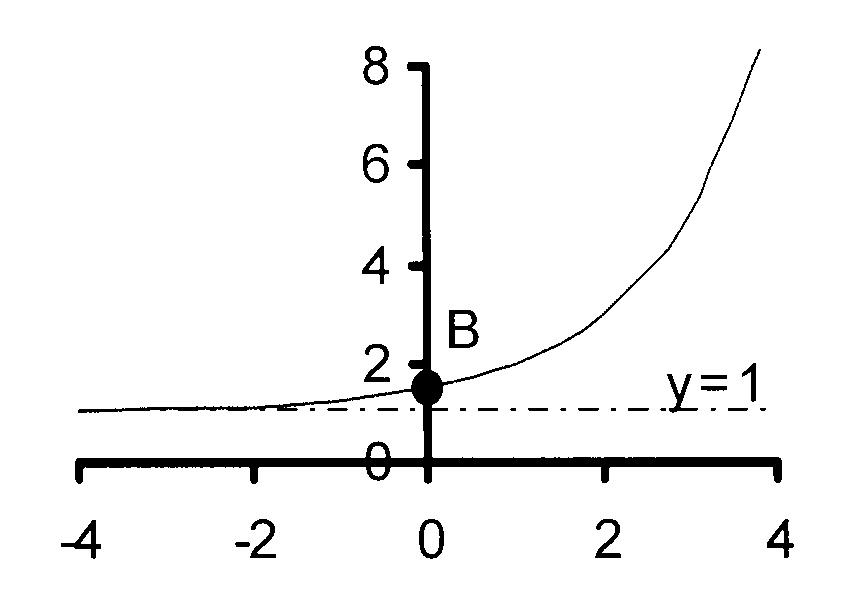
$$ \hspace*{5 mm}\mathrm{\kern3mmy = 2^{x + p} + q\kern2mm\ } $$
B is the point (0 ; 1,5)
[ A 2.1 ]
2.2
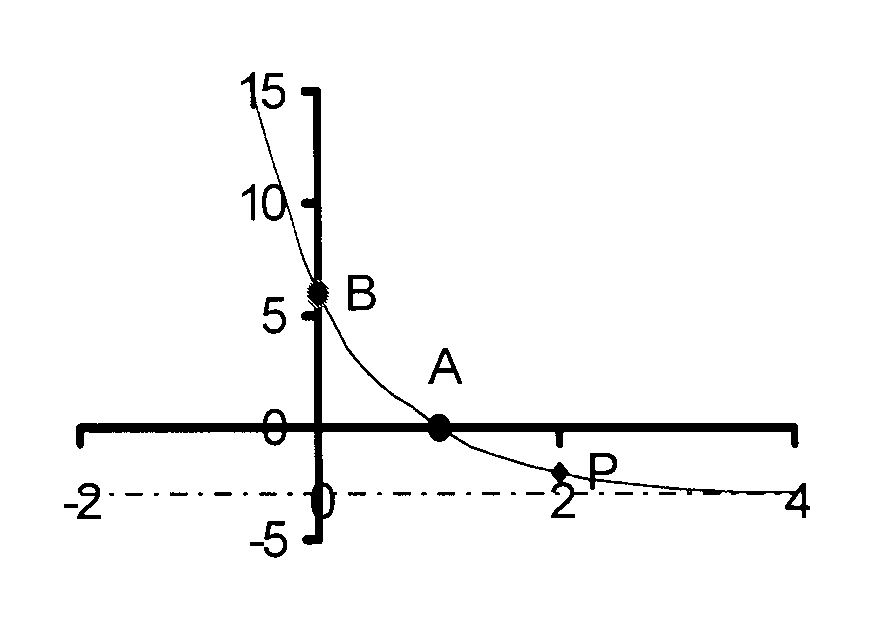
$$ \hspace*{5 mm}\mathrm{\kern3mmy = \Big(\frac{1}{3}\Big)^{x + p} + q\kern2mm\ } $$
Horizontal asymptote : y = − 3 and A(1 ; 0)
B is the point (0 ; 6) and P(2 ; − 2)
[ A 2.2 ]
2.3
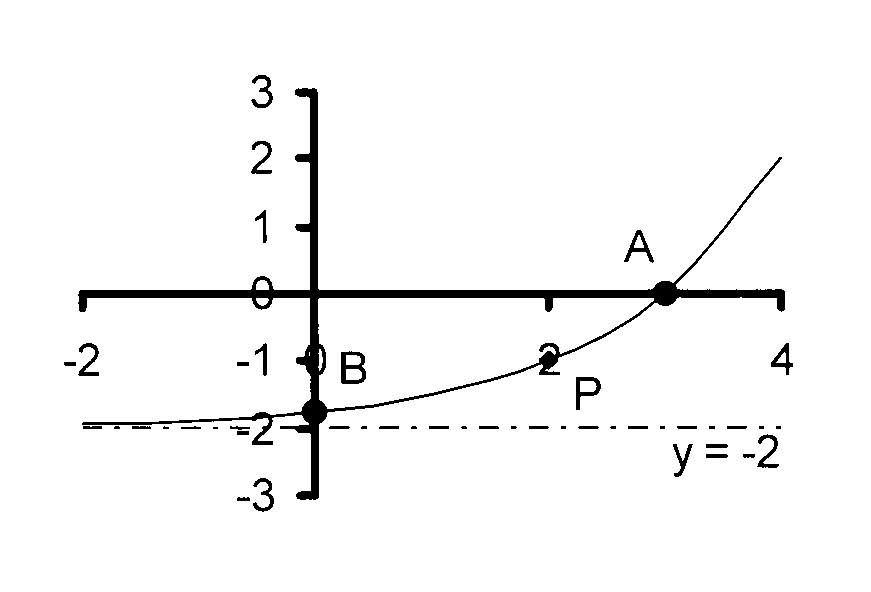
$$ \hspace*{5 mm}\mathrm{\kern3mmy = 2^{x + p} + q\kern2mm\ } $$
Given : A(3 ; 0), B(0 ; −1,75) and P(2 ; − 1)
[ A 2.3 ]
2.4
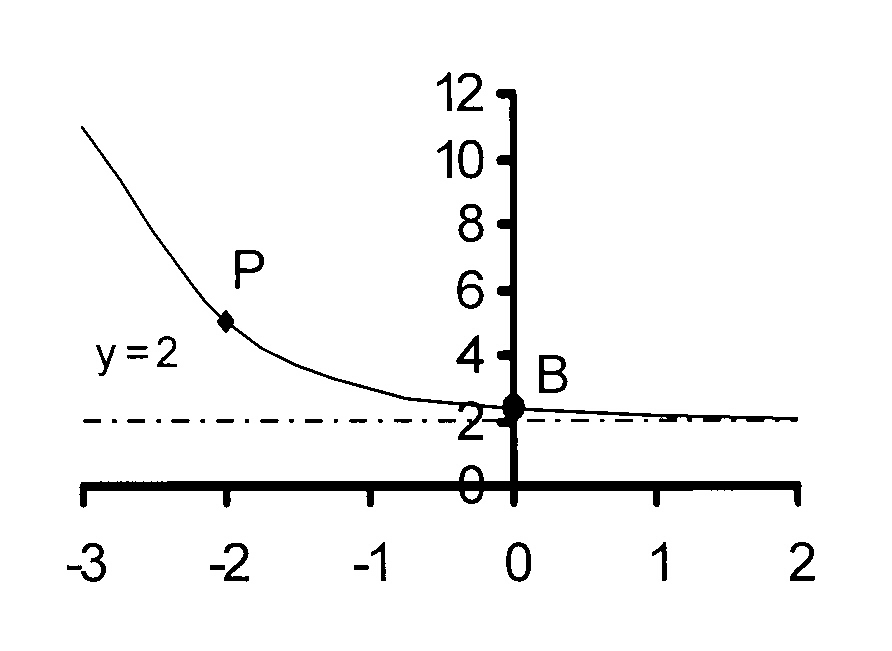
$$ \hspace*{5 mm}\mathrm{\kern3mmy = \Big(\frac{1}{2}\Big)^{x + p} + q\kern2mm\ } $$
Given : B(0 ; 2,33) and P(−2 ; 5)
[ A 2.4 ]
2.5
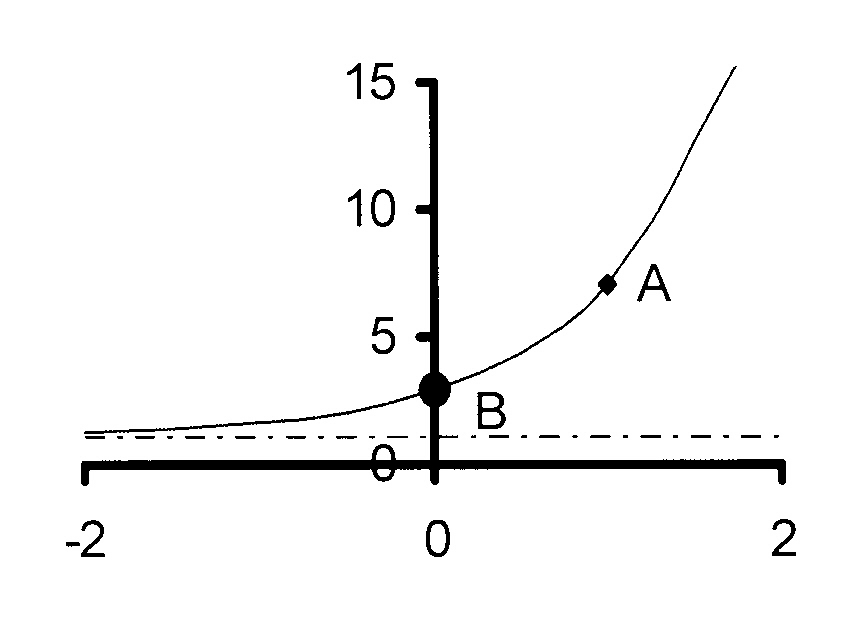
$$ \hspace*{5 mm}\mathrm{\kern3mmy = a.b^x + q and y = 1\kern2mm\ } $$
Given : A(1 ; 7) and B(0 ; 3)
[ A 2.5 ]
2.6
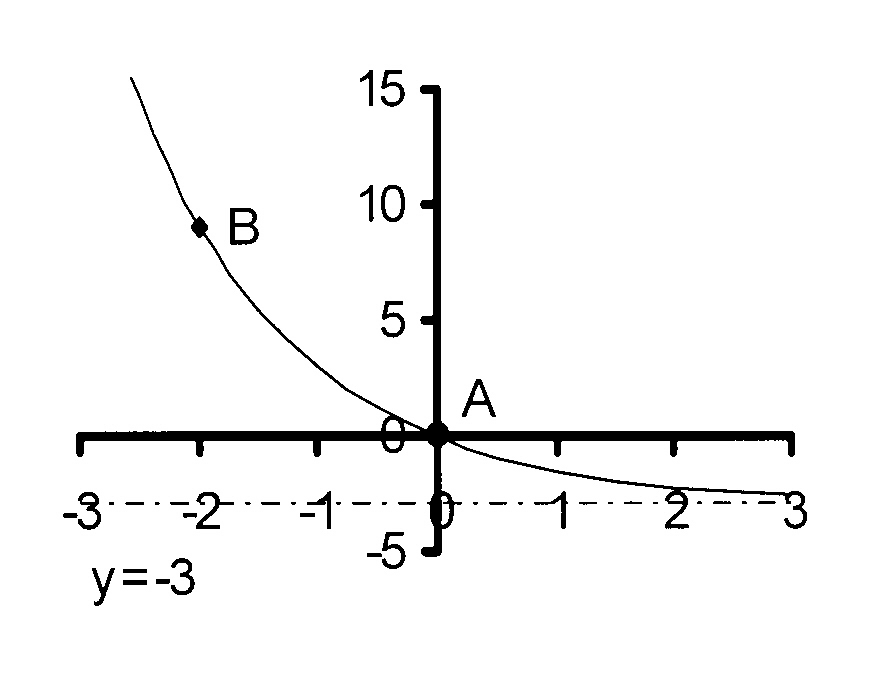
$$ \hspace*{5 mm}\mathrm{\kern3mmy = a.b^x + q\kern2mm\ } $$
Given : A(0 ; 0) and B(− 2 ; 9)
[ A 2.6 ]
The figure shows the graph of
y = 4x − 1 − 2
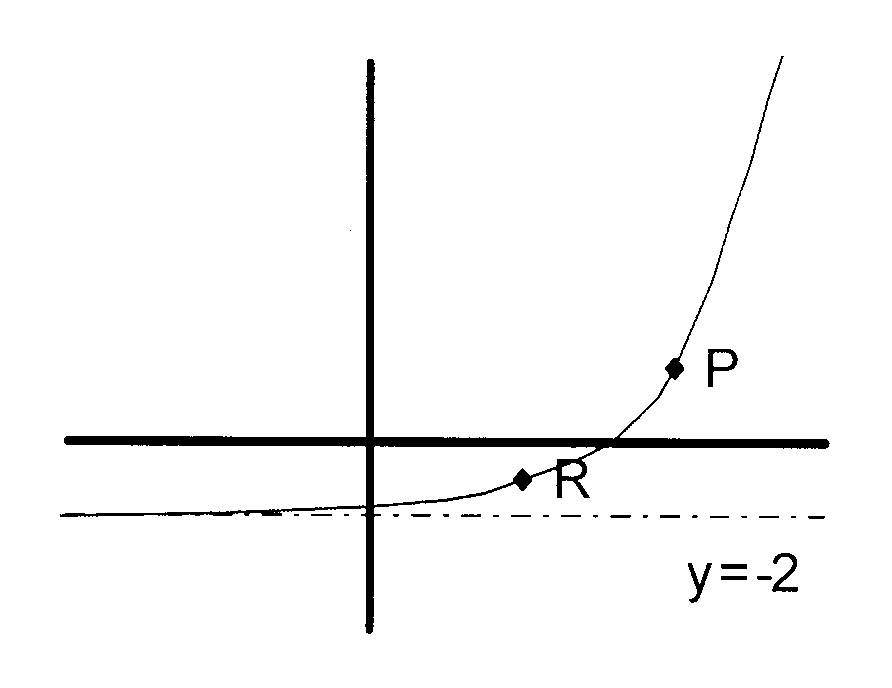
3.1 Calculate the intercepts on
the axes.
[ A 3.1 ]
3.2 Calculate the value of p if P(2;p) is
a point on the graph.
[ A 3.2 ]
3.3 Calculate the value of r if R(r;−1) is
a point on the graph.
[ A 3.3 ]
3.4 For which values of x will
4
x − 1 − 2 > 0?
[ A 3.4 ]
3.5 Write down the domain of
the function.
[ A 3.5 ]
3.6 Write down the range of
the function.
[ A 3.6 ]
The figure shows the graph of
y = 2− x + 1 + 2
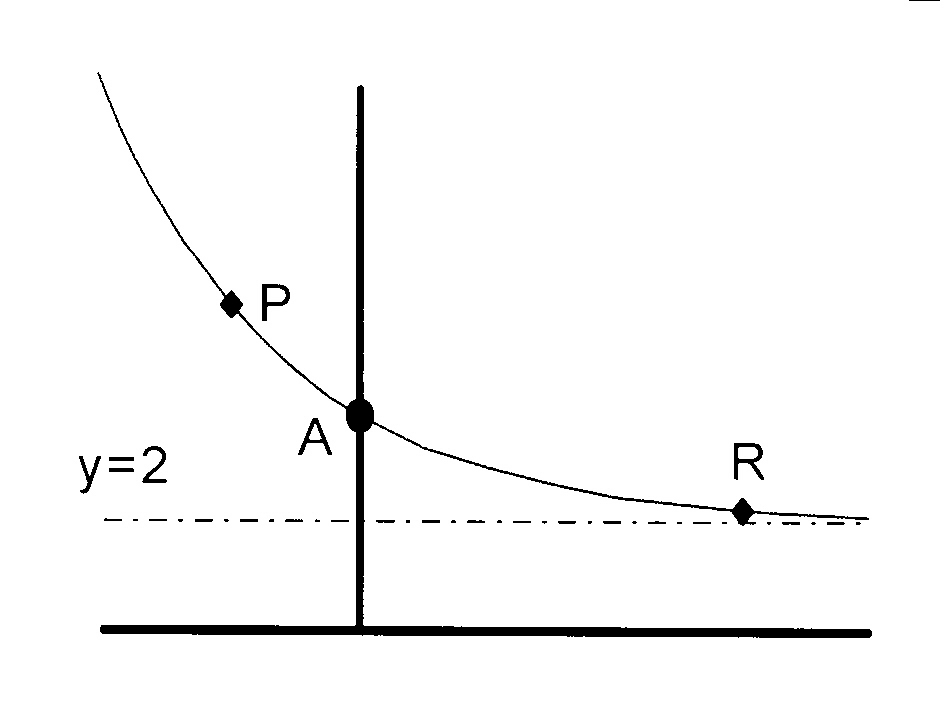
4.1 Calculate the intercepts on
the axes.
[ A 4.1 ]
4.2 Calculate the value of p if P(-1 ; p)
is a point on the graph.
[ A 4.2 ]
4.3 Calculate the value of r if R(r ; 2,25)
is a point on the graph.
[ A 4.3 ]
4.4 Write down the domain of
the function.
[ A 4.4 ]
4.5 Write down the range of
the function.
[ A 4.5 ]
4.6 For which values of x will
the function be positive?.
[ A 4.6 ]
4.7 The function h(x) is formed
when the function above is
translated 4 units downwards.
Write down the equation of
the function h(x).
[ A 4.7 ]
The figure shows the graph of
$$ \hspace*{5 mm}\mathrm{\kern3mmy = \Big(\frac{1}{2}\Big)^{x − 1} − 4\kern2mm\ } $$
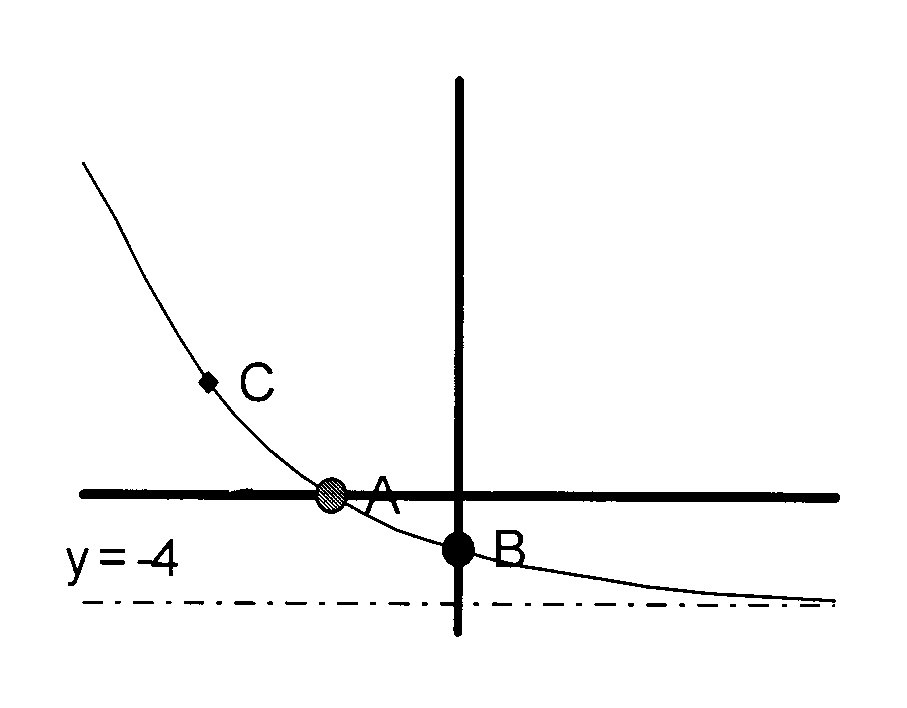
5.1 Calculate the intercepts on
the axes.
[ A 5.1 ]
5.2 Calculate the value of c if C(c ; 4)
is a point on the graph.
[ A 5.2 ]
5.3 Write down the domain of
the function.
[ A 5.3 ]
5.4 Write down the range of
the function.
[ A 5.4 ]
5.5 For which values of x will
$$ \hspace*{12 mm}\mathrm{\kern3mmy = \Big(\frac{1}{2}\Big)^{x − 1} − 4 > 0?\kern2mm\ } $$
[ A 5.5 ]
5.6 The function h(x) is formed
when the function above is
translated 2 units upwards.
Write down the equation of
the function h(x).
[ A 5.6 ]
The figure shows the graph of
$$ \hspace*{5 mm}\mathrm{\kern3mmy = \Big(\frac{1}{3}\Big)^{x + p} + q\kern2mm\ } $$
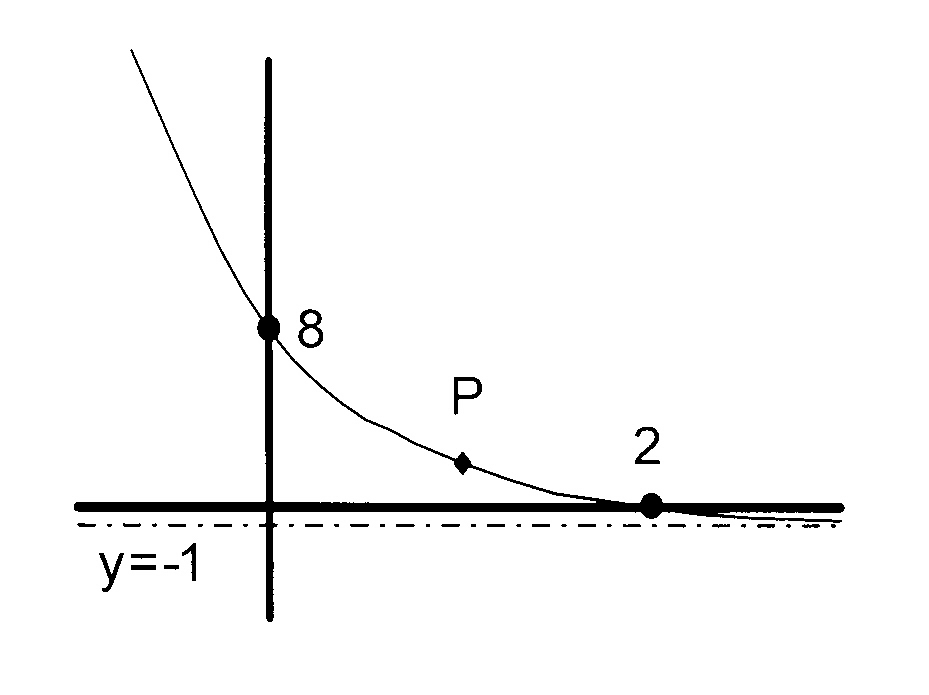
6.1 Calculate the values of p and q.
[ A 6.1 ]
6.2 Calculate the value of p if P(p ; 2)
is a point on the graph.
[ A 6.2 ]
6.3 Write down the domain of
the function.
[ A 6.3 ]
6.4 Write down the range of
the function.
[ A 6.4 ]
6.5 The function h(x) is formed
when the function above is
translated 3 units upwards.
Write down the equation of
the function h(x).
[ A 6.5 ]
6.6 Write down the coordinates of
the Y-intercept of h(x).
[ A 6.6 ]
The diagram shows the graph of h(x) = 2
x − 2
P (p ; 30) is a point on the graph of h(x).
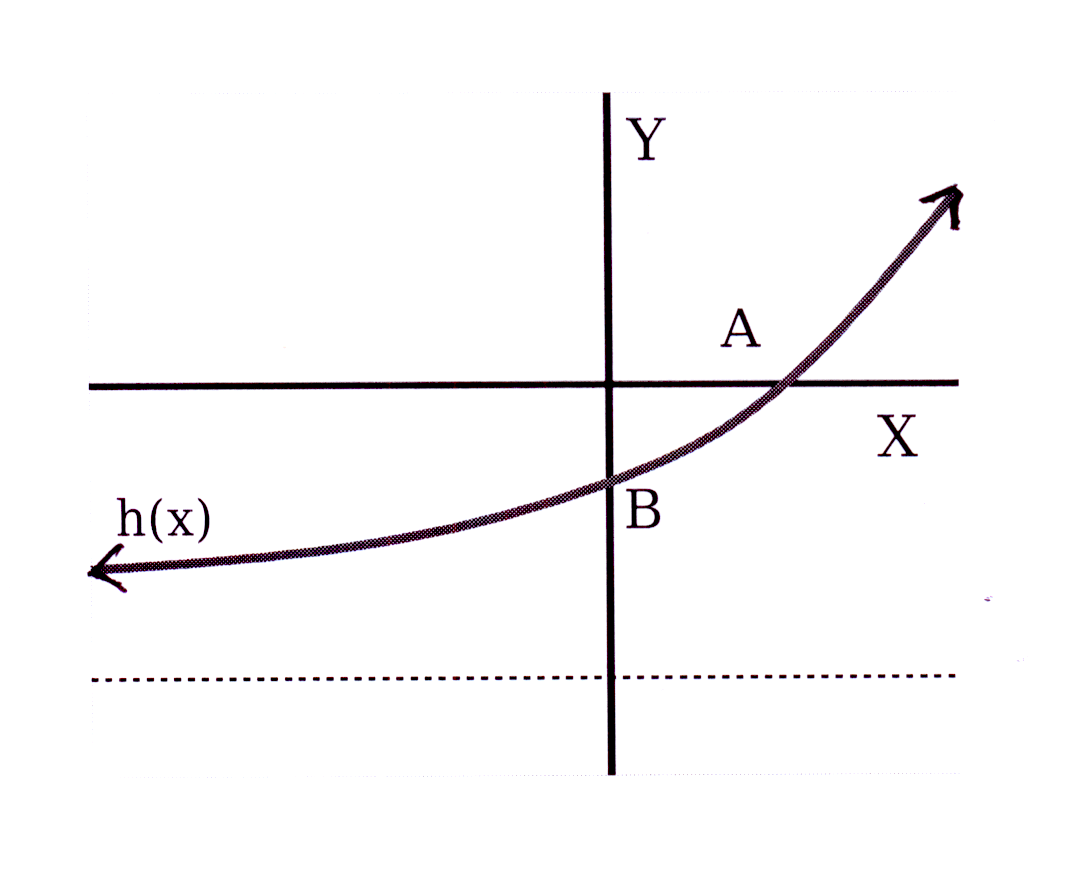
7.1 Write down the equation of the
horizontal asymptote.
[ A 7.1 ]
7.2 Calculate the coordinates of points
the intercepts on the axes.
[ A 7.2 ]
7.3 Determine the value of p.
[ A 7.3 ]
7.4 For which values of x will h(x) ≤ 30?
[ A 7.4 ]
The diagram shows the graph of
f(x) = p
.2
−x + q
D(−4 ;−12) and E(2 ; e) are points on
the graph of f(x).
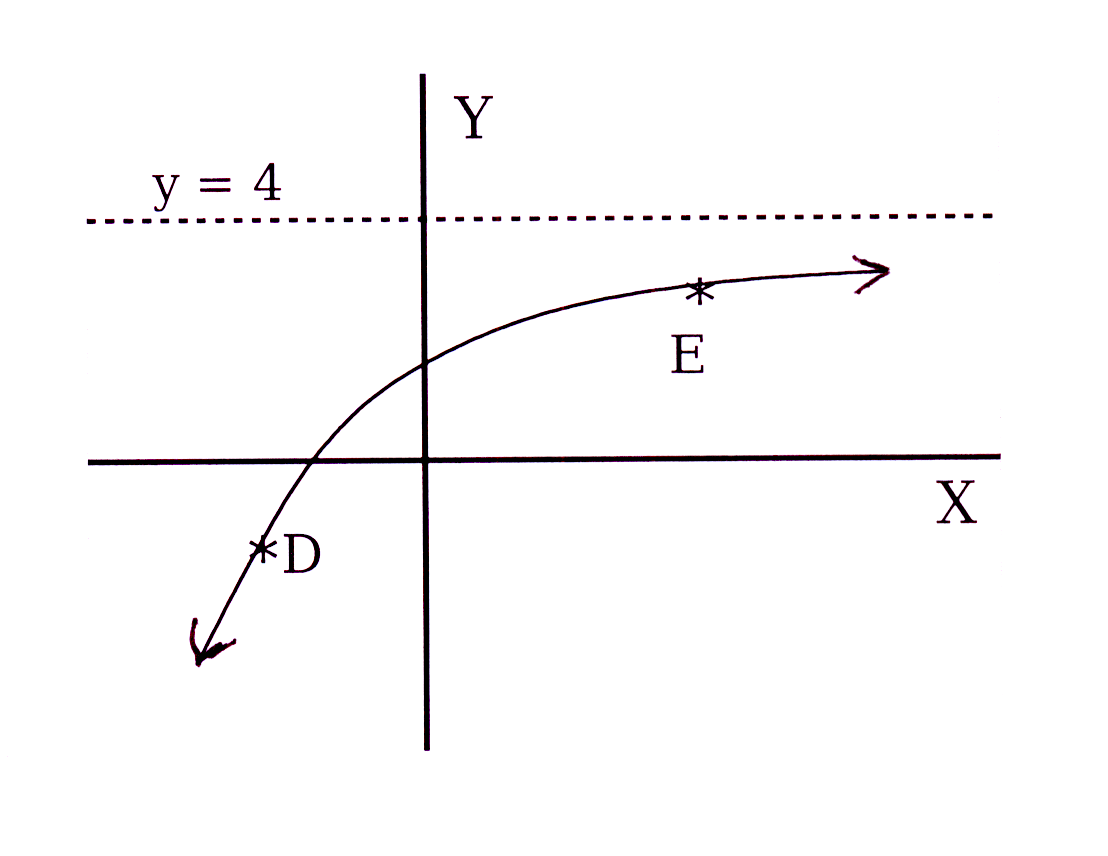
8.1 Write down the equation of the
horizontal asymptote.
[ A 8.1 ]
8.2 Determine the values of p and q
and write down the equation
of f(x).
[ A 8.2 ]
8.3 Determine the value of e.
[ A 8.3 ]
8.4 For which value(s) of x is
f(x) < 3,75?
[ A 8.4 ]
8.5 For which value(s) of x is
f(x) > 0?
[ A 8.5 ]
The diagram shows the graph of
g(x) = 2
x + p + q
A(2 ;11) is a point on the graph of g(x) and
the y-intercept is (0 ; −1).
9.1 Determine the values of p and q and
thus the equation of g(x).
[ A 9.1 ]
9.2 Write down the equation of the
horizontal asymptote.
[ A 9.2 ]
9.3 The graph of h is obtained
by moving the graph of g 4 units
downwards. Write down the
equation of h(x).;
[ A 9.3 ]
9.4 The graph of k is obtained
by moving the graph of g 3 units
to the right. Write down the
equation of k(x).;
[ A 9.3 ]
It is given that f(x) = 2
x.
10.1 The graph of g is obtained
by moving the graph of f 3 units
downwards. Write down the
equation of g(x).
[ A 10.1 ]
10.2 The graph of h is obtained
by moving the graph of f 2 units
to the left. Write down the
equation of h(x).
[ A 10.2 ]
Given that f(x) = 3
−x.
11.1 The graph of g is obtained
by moving the graph of f 2 units
upward.. Write down the
equation of g(x).
[ A 11.1 ]
11.2 The graph of h is obtained
by moving the graph of f 4 units
to the right. Write down the
equation of g(x).
[ A 11.2 ]
Given that f(x) = 5
x + 3.
12.1 The graph of g is obtained
by moving the graph of f 4 units
downwards. Write down the
equation of g(x).
[ A 12.1 ]
12.2 The graph of h is obtained
by moving the graph of f 4 units
to the left. Write down the
equation of h(x).
[ A 12.2 ]
Given that f(x) = − 3
−x + 2.
13.1 The graph of g is obtained
by moving the graph of f 2 units
upward. Write down the
equation of g(x).
[ A 13.1 ]
13.2 The graph of h is obtained
by moving the graph of f 3 units
to the right. Write down the
equation of h(x).
[ A 12.2 ]