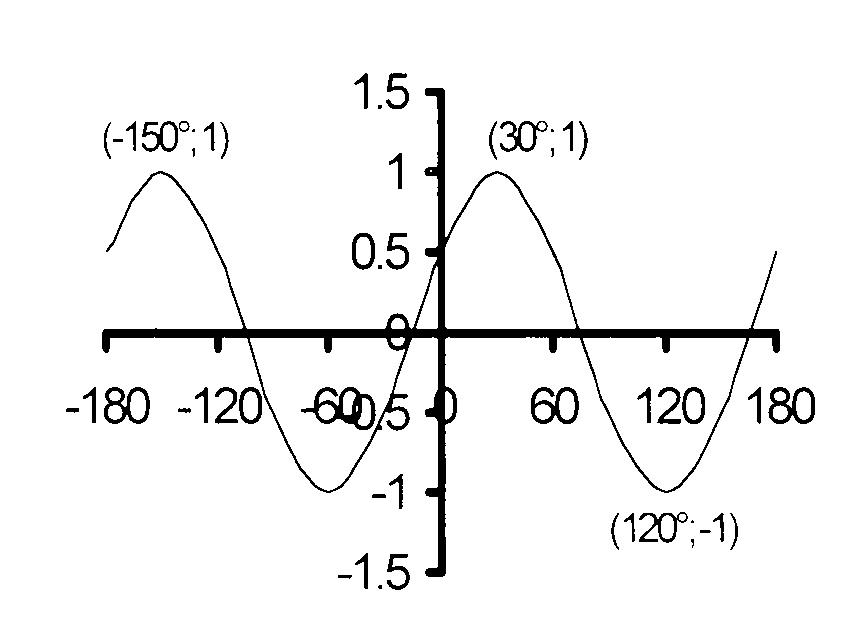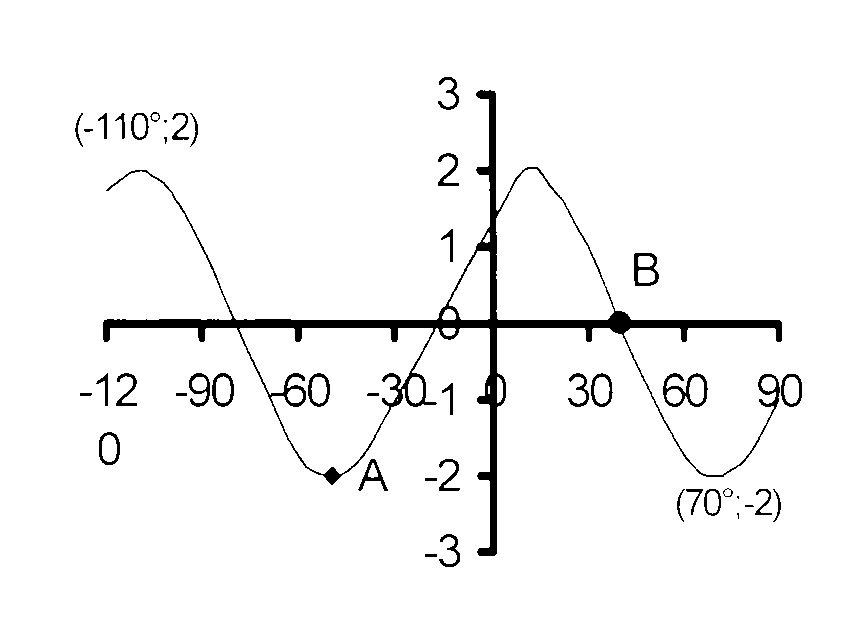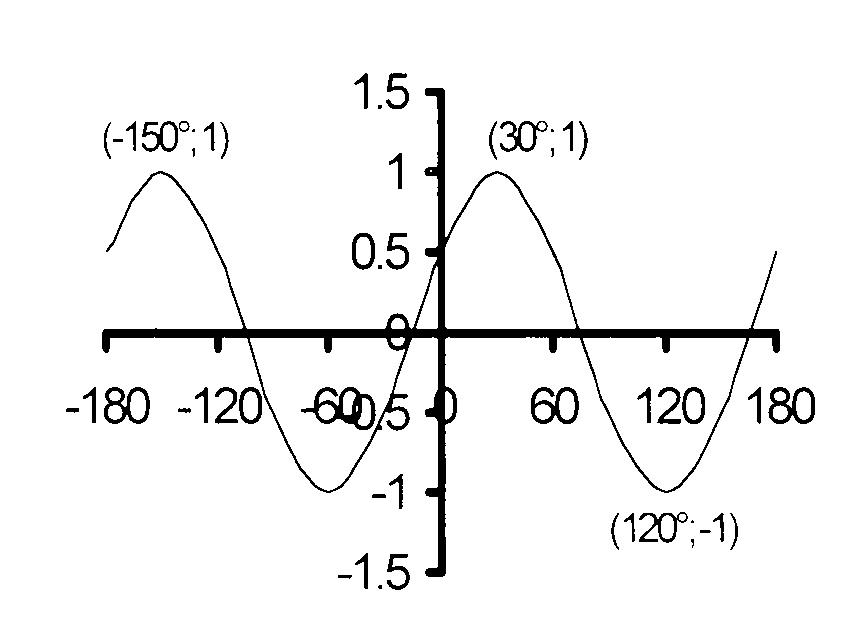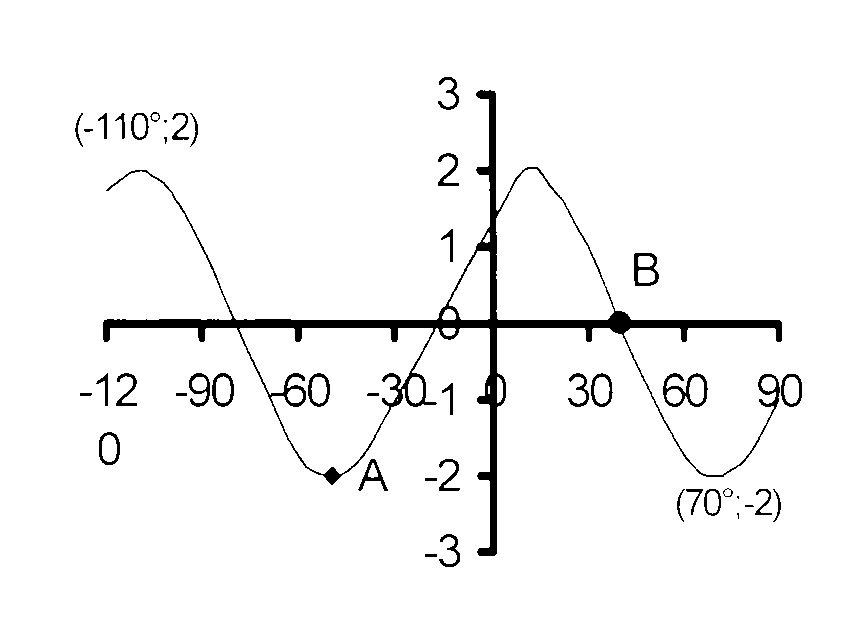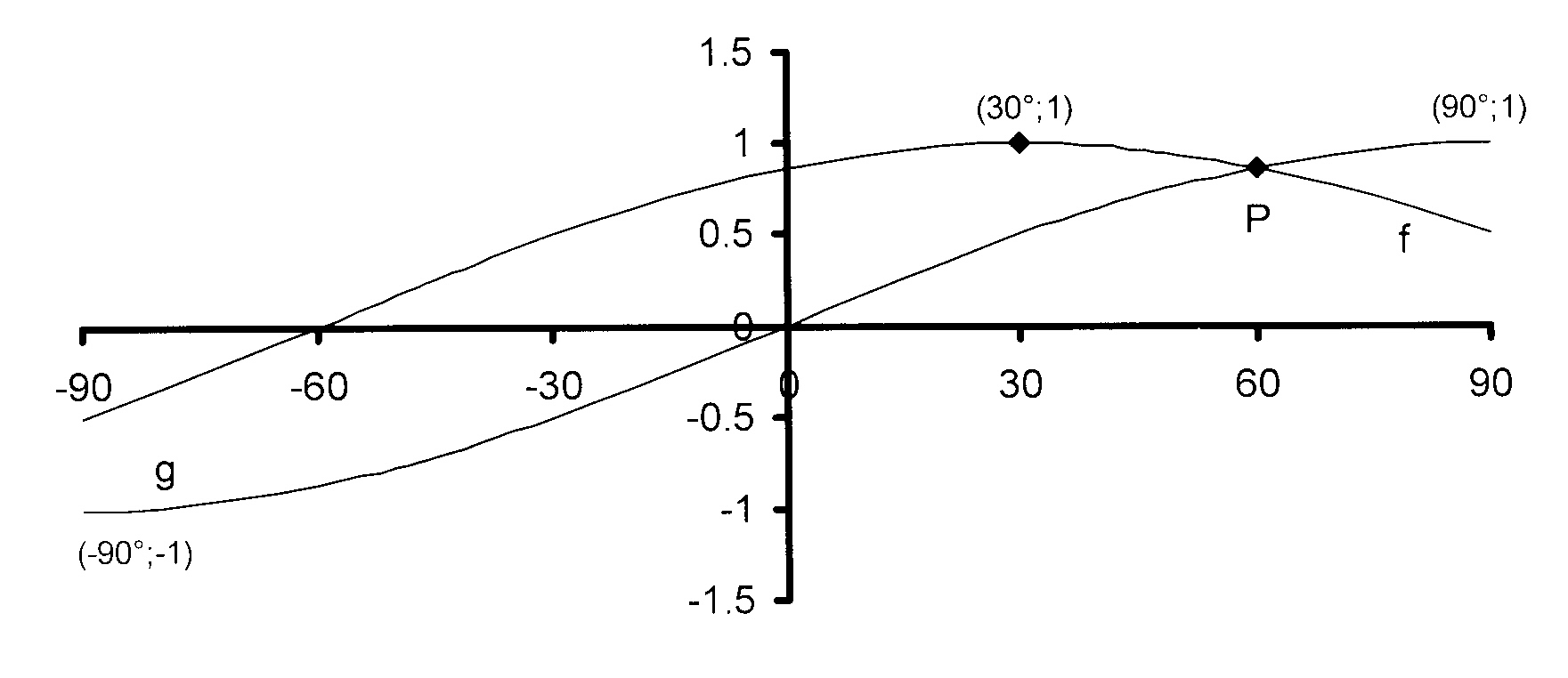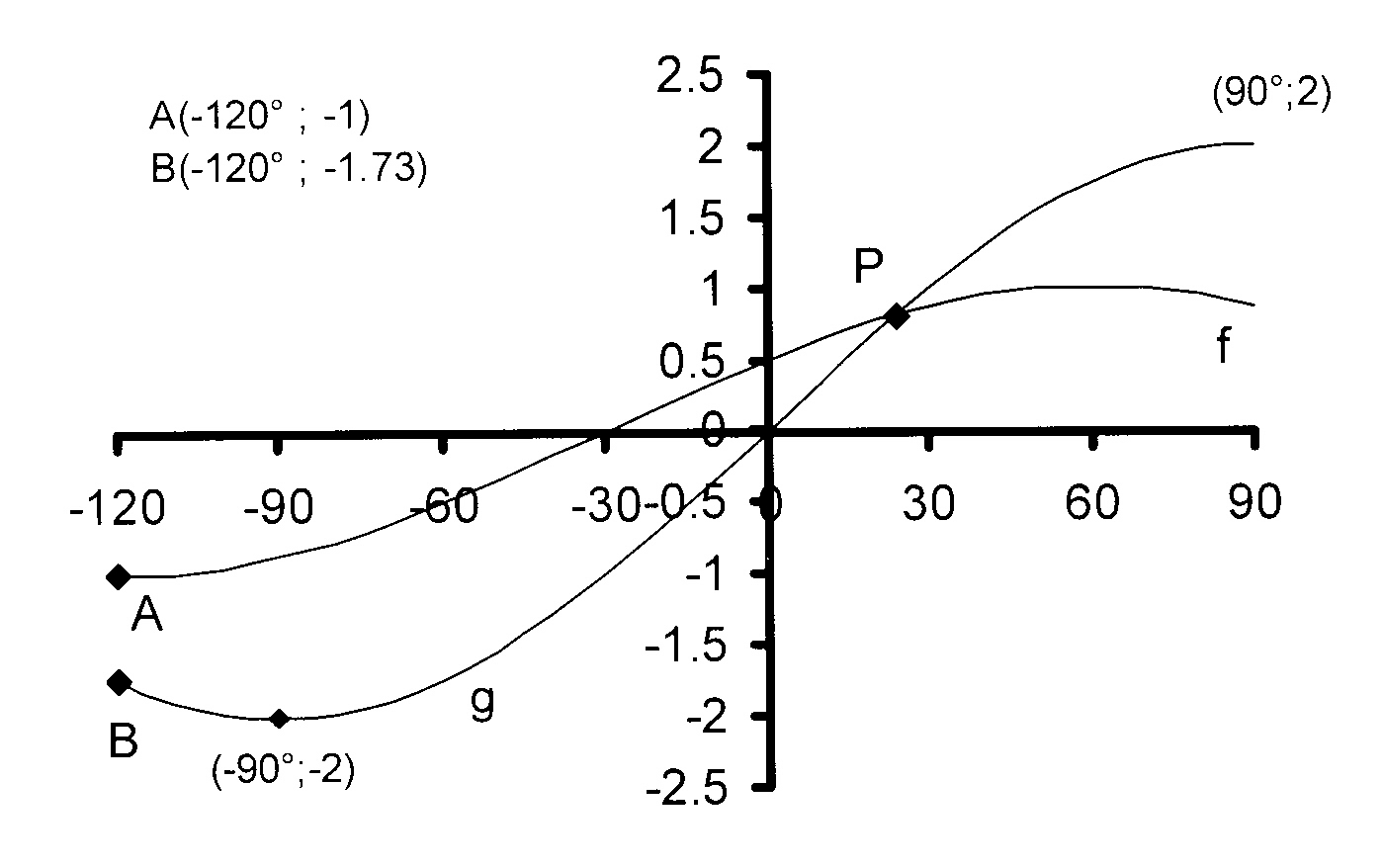Sketch the graphs of the following
functions :
$$ \hspace*{2 mm}\mathrm{1.1\kern3mmy = 2\ sin\ x − 1\ \ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.1 ]
$$ \hspace*{2 mm}\mathrm{1.2\kern3mmy = 1 − 2 sin\ x\ \ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.2 ]
$$ \hspace*{2 mm}\mathrm{1.3\kern3mmy = 2\ cos\ x\ − 1\ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.3 ]
$$ \hspace*{2 mm}\mathrm{1.4\kern3mmy = 1 − 2\ cos\ x\ \ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.4 ]
$$ \hspace*{2 mm}\mathrm{1.5\kern3mmy = sin\ (x − 30°)\ \ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.5 ]
$$ \hspace*{2 mm}\mathrm{1.6\kern3mmy = sin\ (x + 60°)\ \ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.6 ]
$$ \hspace*{2 mm}\mathrm{1.7\kern3mmy = cos\ (x − 60°)\ \ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.7 ]
$$ \hspace*{2 mm}\mathrm{1.8\kern3mmy = cos\ (x + 30°)\ \ and\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.8 ]
$$ \hspace*{2 mm}\mathrm{1.9\kern3mmy = 1 − sin x\ \ and\ \ x ∈ [-90° ; 180°]\kern2mm\ } $$
[ A 1.9 ]
$$ \hspace*{2 mm}\mathrm{1.10\kern3mmy = 3 cos\ x\ − 2\ \ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.10 ]
$$ \hspace*{2 mm}\mathrm{1.11\kern3mmy = sin\ (x − 30°)\ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.11 ]
$$ \hspace*{2 mm}\mathrm{1.12\kern3mmy = cos\ (2x − 60°)\ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.12 ]
$$ \hspace*{2 mm}\mathrm{1.13\kern3mmy = cos\ (x + 30°)\ − 1\ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.13 ]
$$ \hspace*{2 mm}\mathrm{1.14\kern3mmy = sin\ (x + 60°)\ + 1\ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.14 ]
$$ \hspace*{2 mm}\mathrm{1.15\kern3mmy = tan\ x\ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.15 ]
$$ \hspace*{2 mm}\mathrm{1.16\kern3mmy = tan\ x\ =\ 1\ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.16 ]
$$ \hspace*{2 mm}\mathrm{1.17\kern3mmy = tan\ (x + 30°)\ and\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.17 ]
$$ \hspace*{2 mm}\mathrm{1.18\kern3mmy = tan\ 2x\ and\ \ x ∈ [-90° ; 90°]\kern2mm\ } $$
[ A 1.18 ]
The figures show the graphs of the
trigonometric functions given at each
question. Use the information given in
the figure to determine the values of
the unknown variables :
2.1 The graph of y = a sin k(x + p)
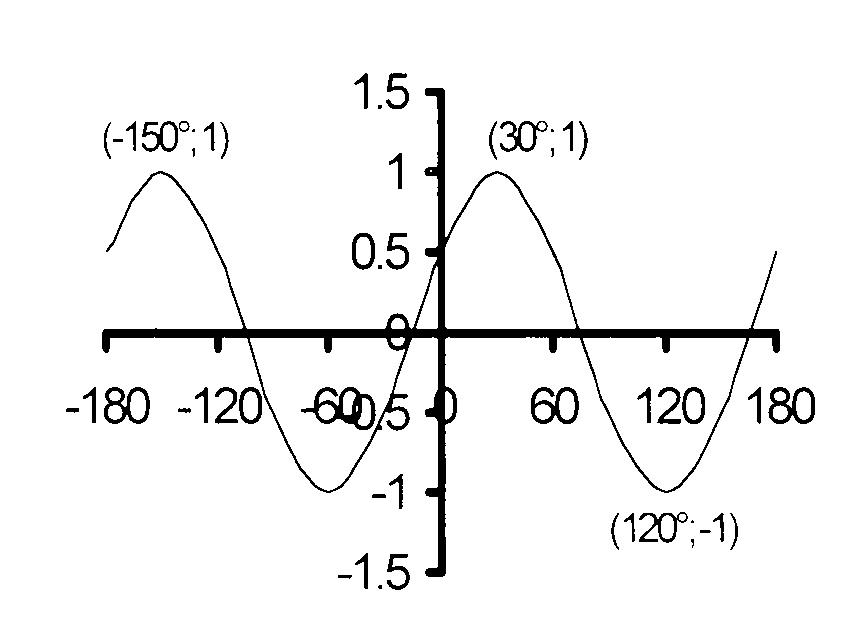 [ A 2.1 ]
2.2
[ A 2.1 ]
2.2 The graph of y = a cos k(x + p)
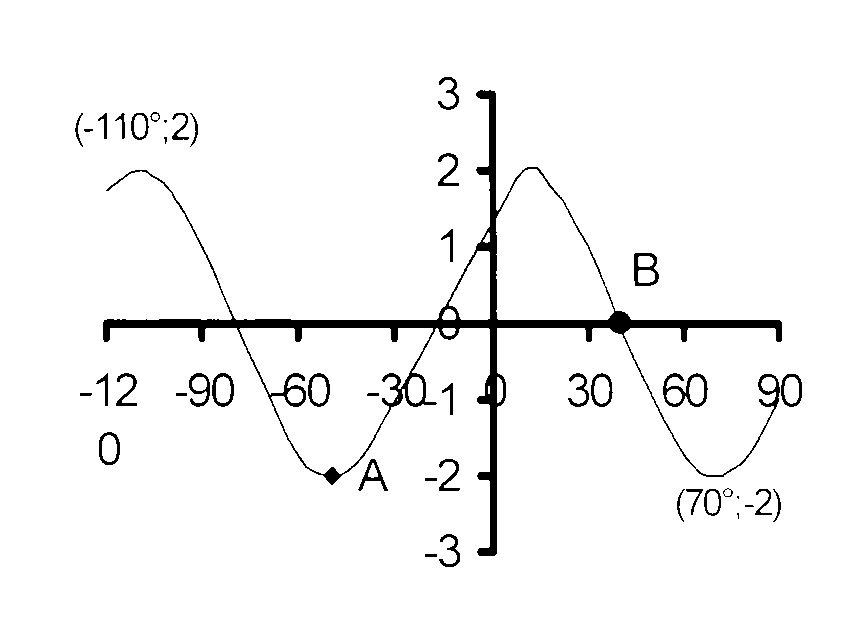 [ A 2.2 ]
2.3
[ A 2.2 ]
2.3 The graph of y = a sin k(x + p)
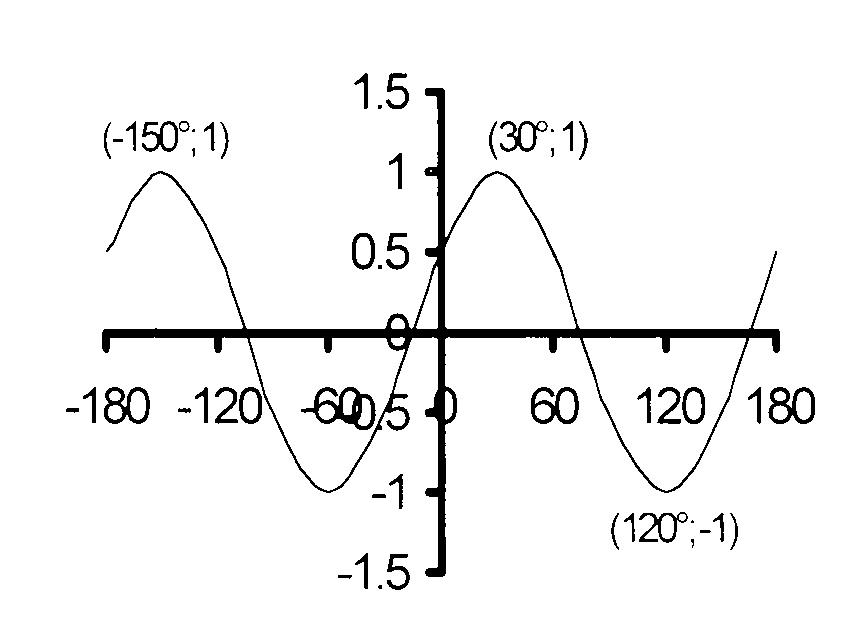 [ A 2.3 ]
2.4
[ A 2.3 ]
2.4 The graph of y = a cos k(x + p)
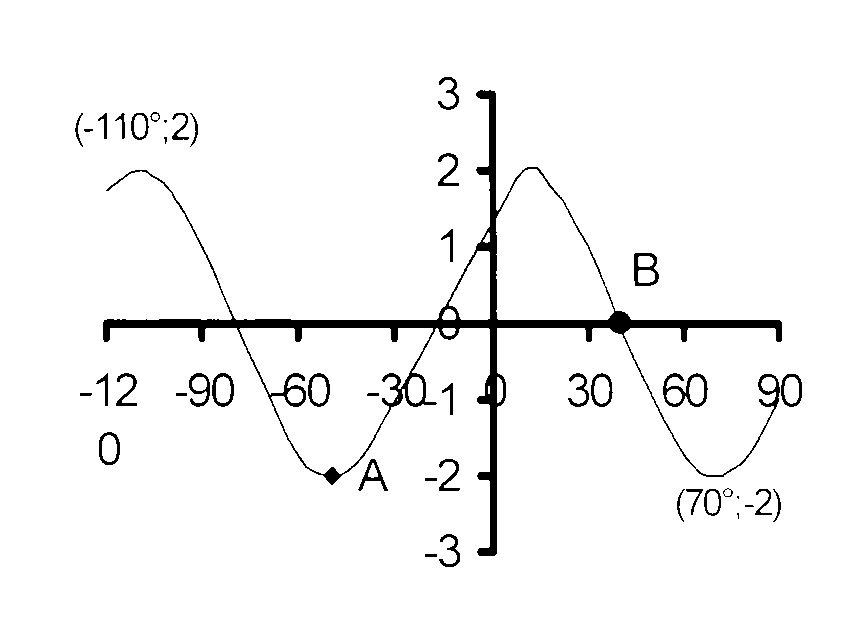 [ A 2.4 ]
2.5
[ A 2.4 ]
2.5 The graph of y = a sin k(x + p)
 [ A 2.5 ]
2.6
[ A 2.5 ]
2.6 The graph of y = a cos k(x + p)
 [ A 2.6 ]
[ A 2.6 ]
3.1 On the same set of axes draw the
graphs of f(x) = sin (x − 30°) and
g(x) = cos 2x for − 180° ≤ x ≤ 180°.
Give the intercepts with the axes.
[ A 3.1 ]
3.2 Give the period of f.
[ A 3.2 ]
3.3 Determine x by calculation if
f(x) = g(x).
[ A 3.3 ]
3.4 For which value(s) of x
will f(x) < -0,5?
[ A 3.4 ]
3.5 For which value(s) of x
will f(x) ≥ 0,5?
[ A 3.5 ]
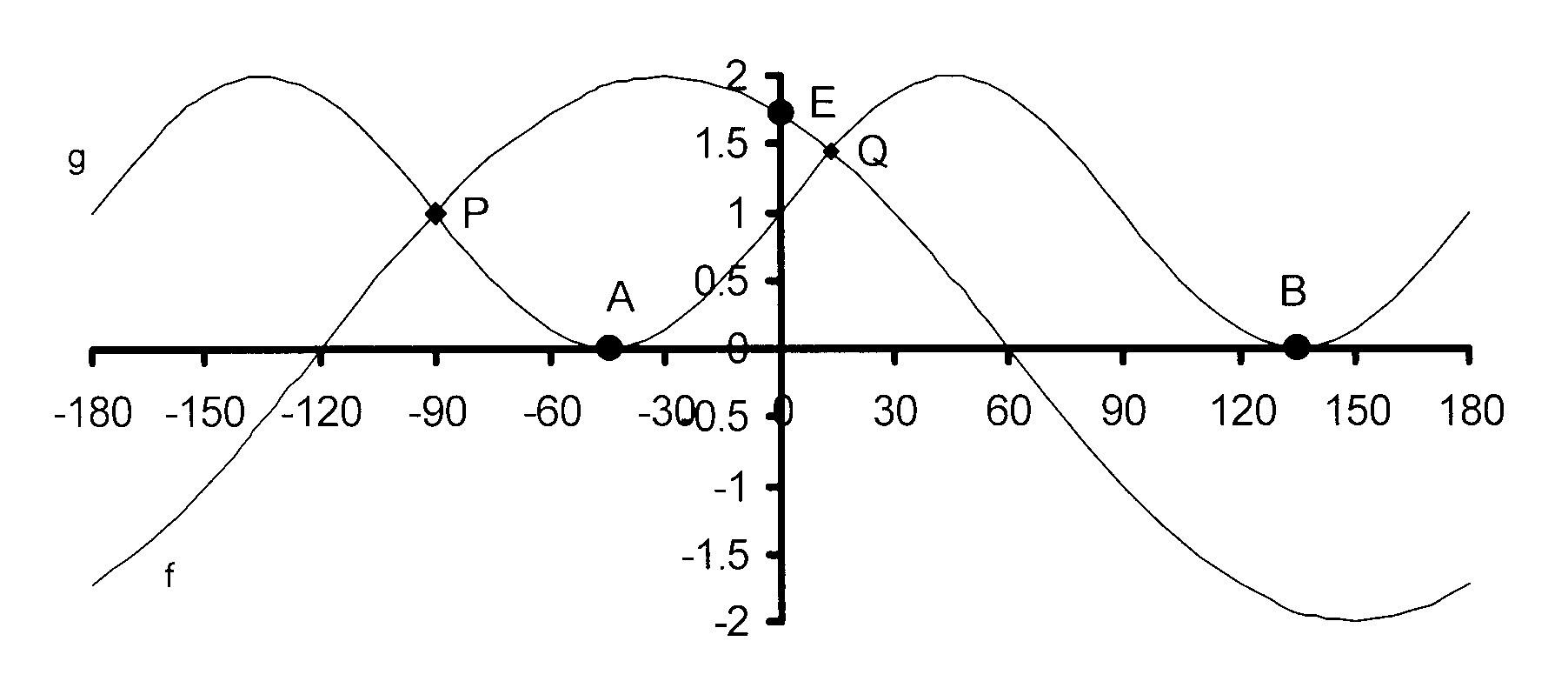
In the figure, the graphs of f(x) = a cos (x + b)
and g(x) = c + sin dx for −180° ≤ x ≤ 180°
are shown.
4.1 Determine the values of a, b, c and d
by using the graphs.
[ A 4.1 ]
4.2 Calculate the value of f(x) if x = 0° without
using a calculator.
[ A 4.2 ]
4.3 Determine x by using the graphs if
4.3.1 g(x) = 2
[ A 4.3.1 ]
4.3.2 f(x) ≥ g(x)
[ A 4.3.2 ]
4.4 The Y-axis is translated to pass
through the turning point of f,
where f(x) reaces a maximum.
Determine an equationfor f in
the form y = . . . with reference to
the new set of axes.
[ A 4.4 ]
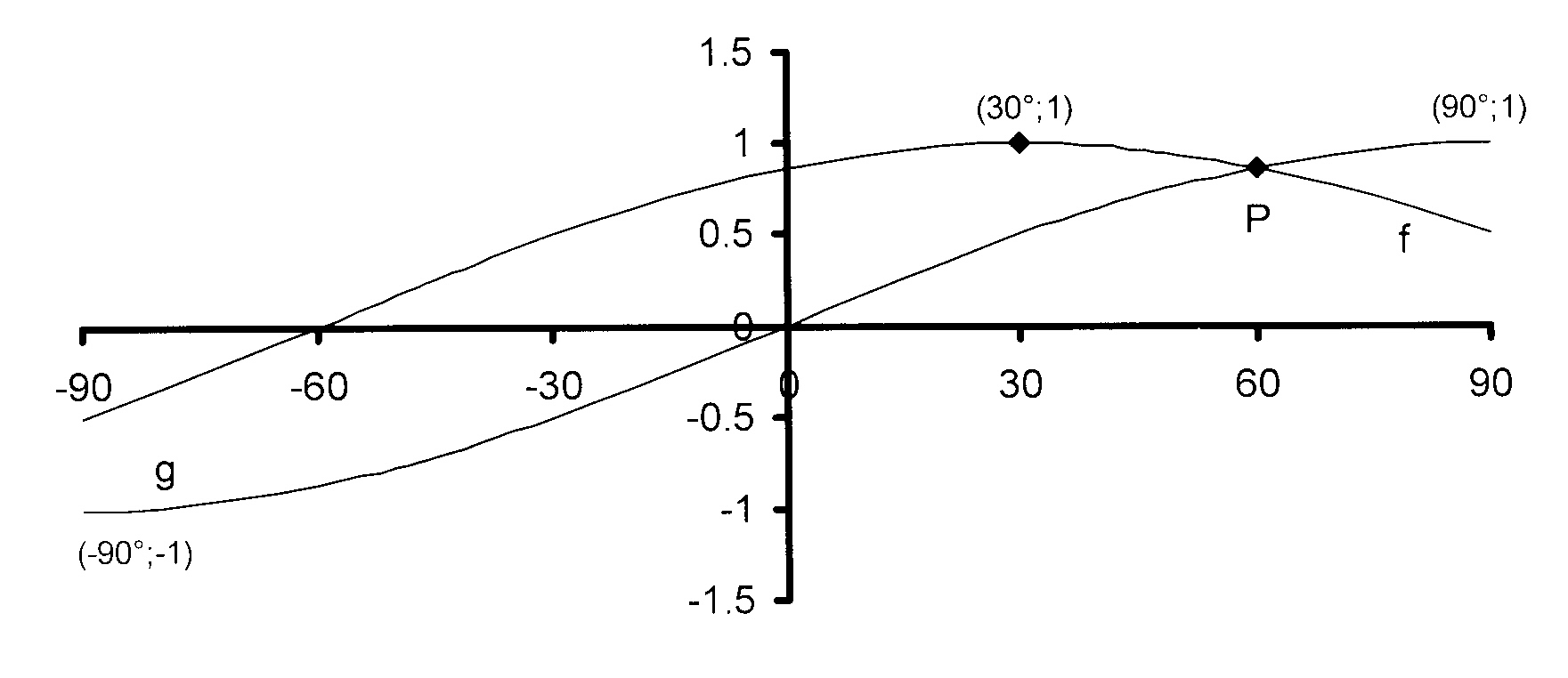
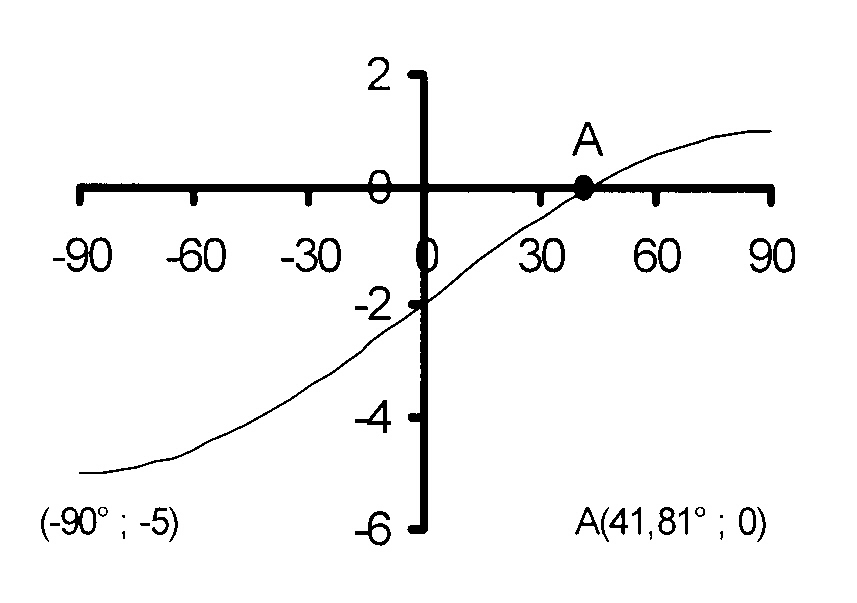
In the figure, the graphs of f(x) = a cos (x + b)
and g(x) = sin cx for −90° ≤ x ≤ 90°
are shown.
5.1 Determine the values of a, b and c
by using the graphs.
[ A 5.1 ]
5.2 Use the graphs to answer the
following questions :
5.2.1 Write down the range of f.
[ A 5.2.1 ]
5.2.2 For what values of x is f(x)
decreasing as x increases?
[ A 5.2.2 ]
5.2.3 If x ∈ [−90° ; 0°], for what values
of x is f(x)
.g(x) ≥ 0?
[ A 5.2.3 ]
5.3 If x ∈ [−90° ; 90°], solve the equation
cos (x − 30°) = sin x and hence
write down the values of x in the
interval [−90° ; 90°] for which g(x) > f(x).
[ A 5.3 ]
5.4 The graph of h(x) is formed by
translating the graph of g(x) 60° to
the left. Wrire down the equation
of h(x).
[ A 5.4 ]
5.5 How can the graph of f(x) be
translated to form the graph of g(x)?
[ A 5.5 ]
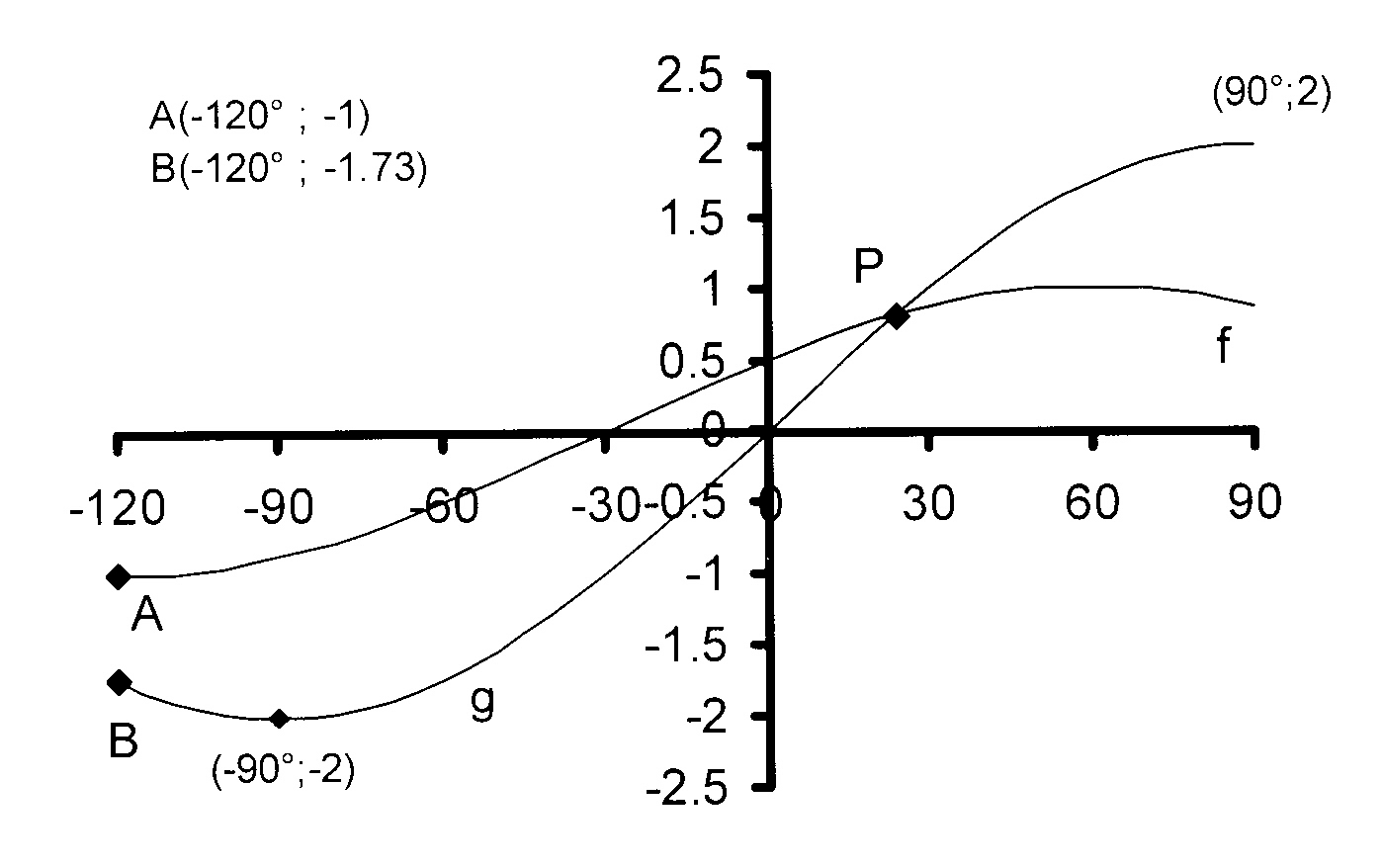
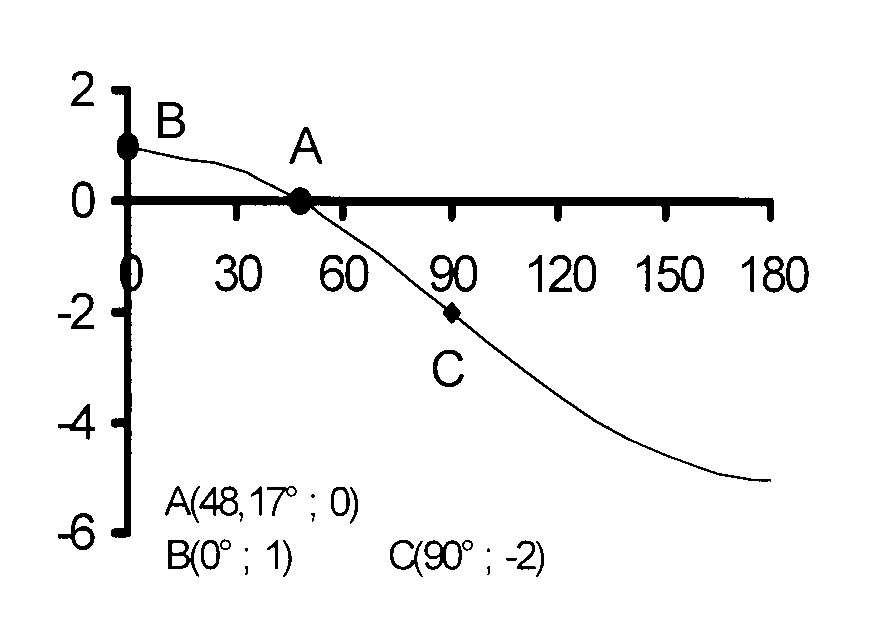
In the figure, the graphs of f(x) = a cos (x + b)
and g(x) = c sin dx for −120° ≤ x ≤ 90°
are shown.
6.1 Write down the amplitude and
period of g.
[ A 6.1 ]
6.2 Determine the values of a, b, c
and d.
[ A 6.2 ]
6.3 Write down the range of g.
[ A 6.3 ]
6.4 Write down the value(s) of x < 0°
for which f(x)
.g(x) ≥ 0.
[ A 6.4 ]
6.5 If the Y-axis is moved to the left so
as to pass through the point of
intersection of the given cosine curve
and the X-axis, which function is now
represented by the curve that initially
represented the given sine function?
[ A 6.4 ]
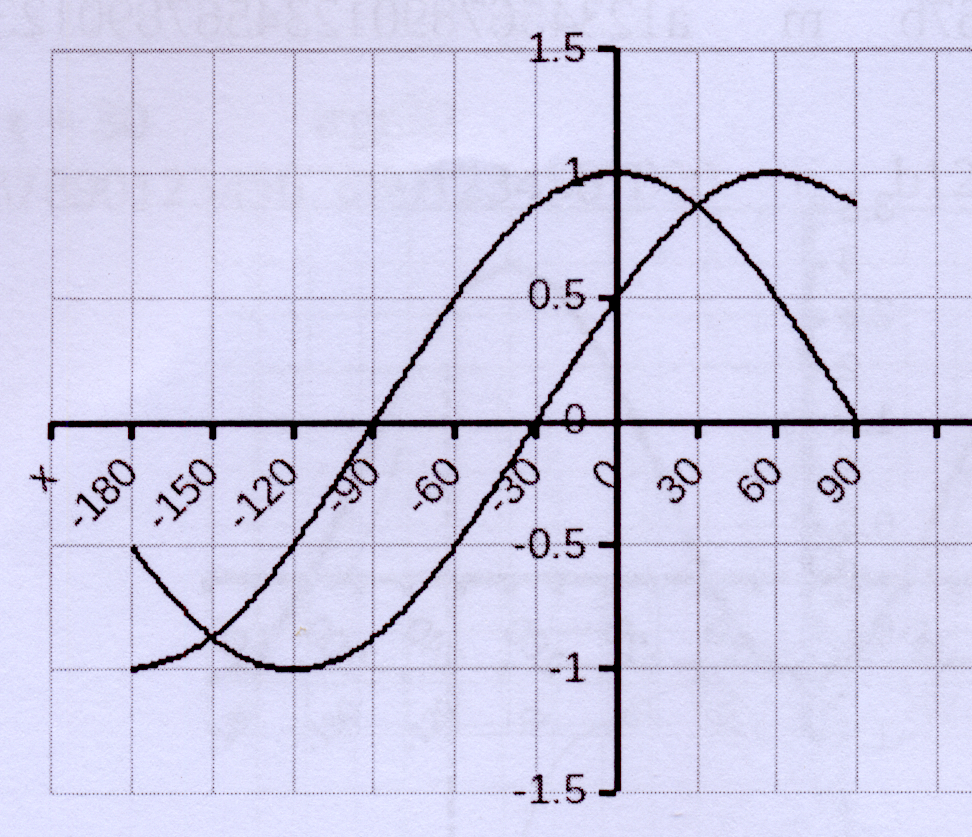
In the diagram, the graphs of f(x) = cos x and
and g(x) = sin (x + b) are drawn for the
interval −180° ≤ x ≤ 90°
7.1 Write down the value of b.
[ A 7.1 ]
7.2 Write down the period of g.
[ A 7.2 ]
7.3 Write down the value(s) of x in
the interval − 180° ≤ x ≤ 90° for
which f(x) − g(x) = 0
[ A 7.3 ]
7.4 For which values of x in
the interval − 180° ≤ x ≤ 90°
7.4.1 is sin (90° − x) > g(x)?
[ A 7.4.1 ]
7.4.2 is f(x)
.g(x) < 0?
[ A 7.4.2 ]
7.4.3 is f(x)
.g(x) ≥ 0?
[ A 7.4.3 ]
7.5 The graph of h is obtained by shifting
f 3 units upwards. Determine the range of h.
[ A 7.5 ]
7.6 The graph of p is obtained by shifting
f 3 units downwards. Write down the
equation of p.
[ A 7.6 ]
7.7 The graph of q is obtained by shifting
f 30° to the left. Write down the
equation of p.
[ A 7.7 ]