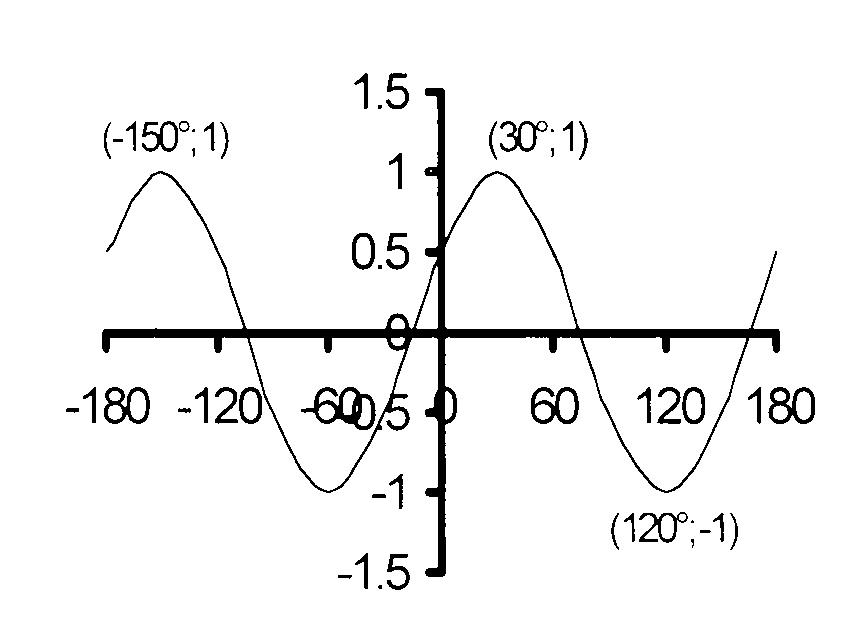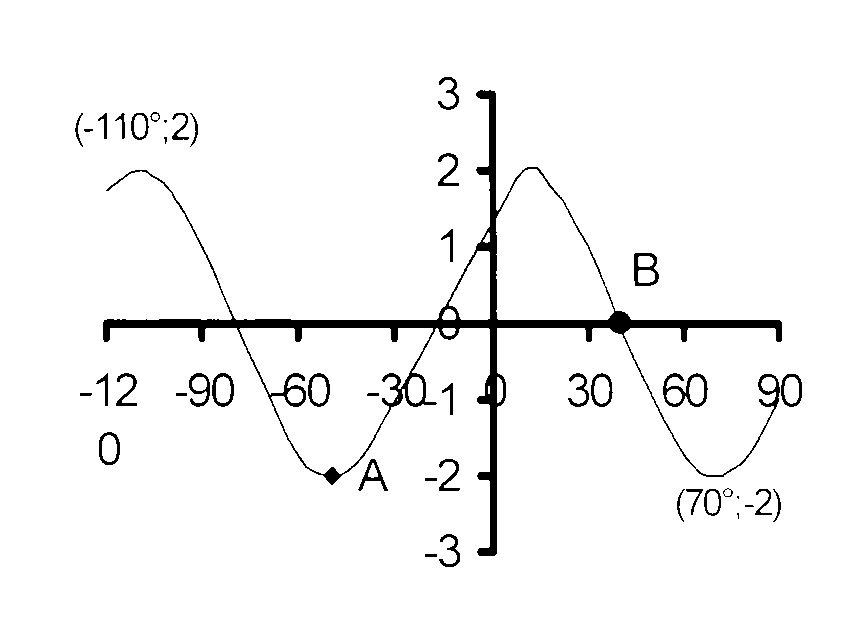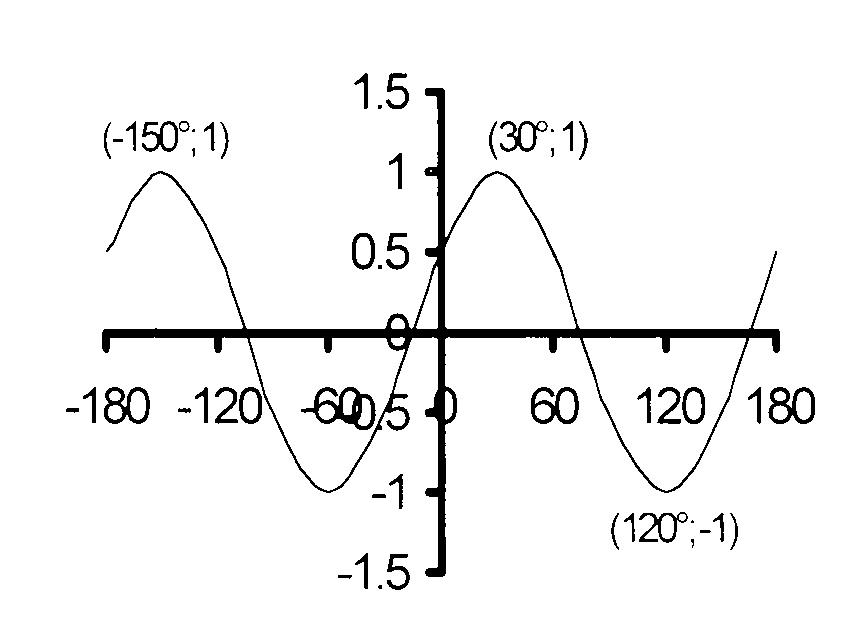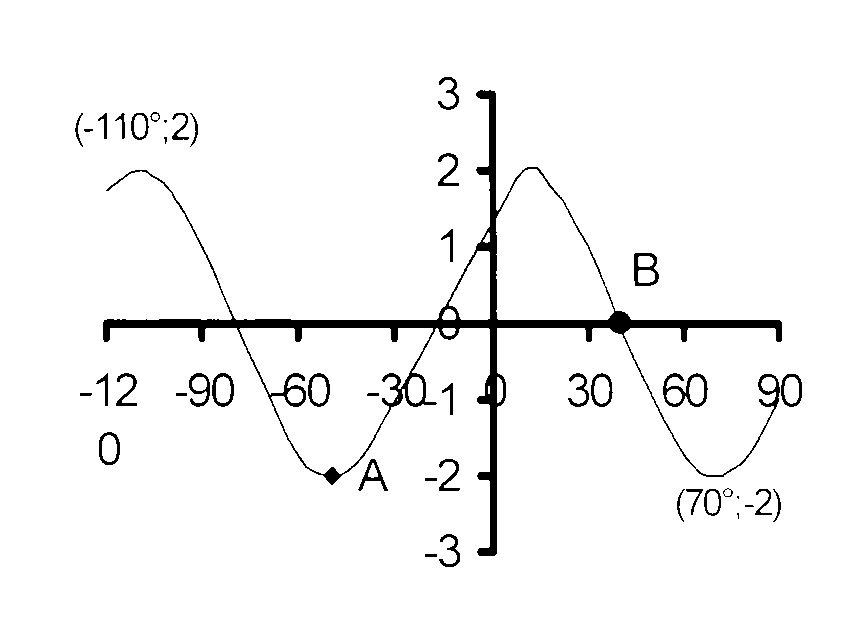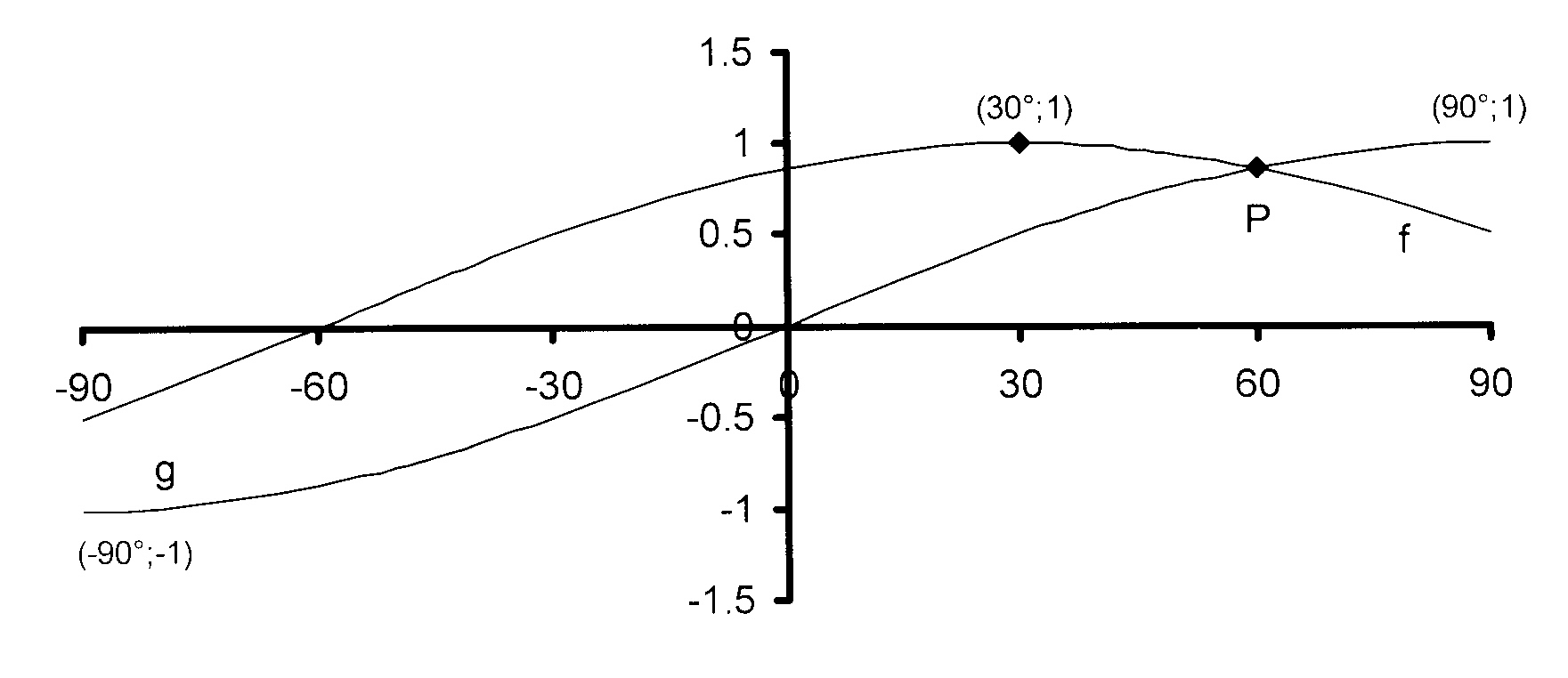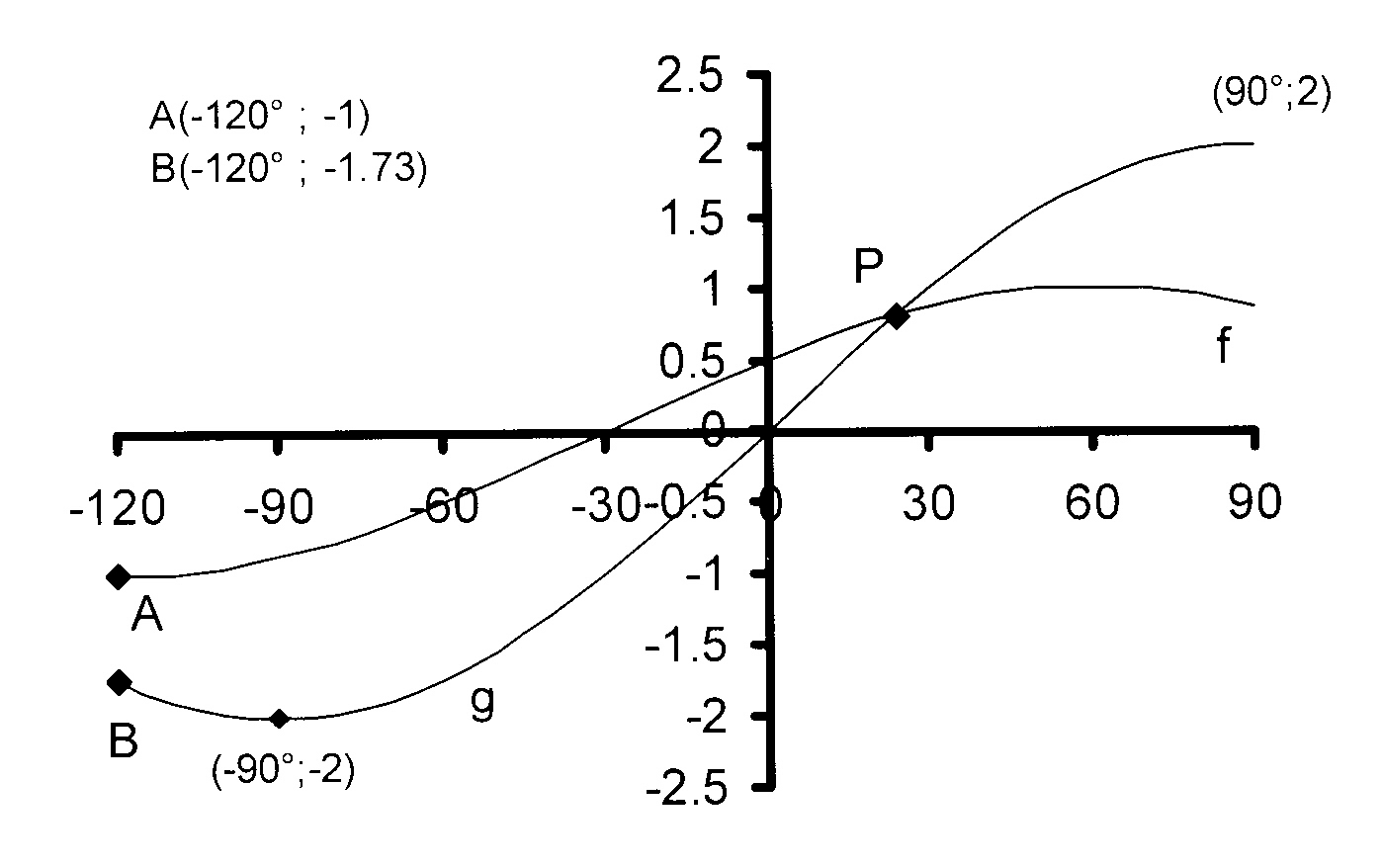Skets die grafieke van die volgende
funksies :
$$ \hspace*{2 mm}\mathrm{1.1\kern3mmy = 2\ sin\ x − 1\ \ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.1 ]
$$ \hspace*{2 mm}\mathrm{1.2\kern3mmy = 1 − 2 sin\ x\ \ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.2 ]
$$ \hspace*{2 mm}\mathrm{1.3\kern3mmy = 2\ cos\ x\ − 1\ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.3 ]
$$ \hspace*{2 mm}\mathrm{1.4\kern3mmy = 1 − 2\ cos\ x\ \ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.4 ]
$$ \hspace*{2 mm}\mathrm{1.5\kern3mmy = sin\ (x − 30°)\ \ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.5 ]
$$ \hspace*{2 mm}\mathrm{1.6\kern3mmy = sin\ (x + 60°)\ \ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.6 ]
$$ \hspace*{2 mm}\mathrm{1.7\kern3mmy = cos\ (x − 60°)\ \ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.7 ]
$$ \hspace*{2 mm}\mathrm{1.8\kern3mmy = cos\ (x + 30°)\ \ en\ \ x ∈ [-360° ; 360°]\kern2mm\ } $$
[ A 1.8 ]
$$ \hspace*{2 mm}\mathrm{1.9\kern3mmy = 1 − sin x\ \ en\ \ x ∈ [-90° ; 180°]\kern2mm\ } $$
[ A 1.9 ]
$$ \hspace*{2 mm}\mathrm{1.10\kern3mmy = 3 cos\ x\ − 2\ \ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.10 ]
$$ \hspace*{2 mm}\mathrm{1.11\kern3mmy = sin\ (x − 30°)\ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.11 ]
$$ \hspace*{2 mm}\mathrm{1.12\kern3mmy = cos\ (2x − 60°)\ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.12 ]
$$ \hspace*{2 mm}\mathrm{1.13\kern3mmy = cos\ (x + 30°)\ − 1\ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.13 ]
$$ \hspace*{2 mm}\mathrm{1.14\kern3mmy = sin\ (x + 60°)\ + 1\ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.14 ]
$$ \hspace*{2 mm}\mathrm{1.15\kern3mmy = tan\ x\ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.15 ]
$$ \hspace*{2 mm}\mathrm{1.16\kern3mmy = tan\ x\ =\ 1\ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.16 ]
$$ \hspace*{2 mm}\mathrm{1.17\kern3mmy = tan\ (x + 30°)\ en\ \ x ∈ [-180° ; 180°]\kern2mm\ } $$
[ A 1.17 ]
$$ \hspace*{2 mm}\mathrm{1.18\kern3mmy = tan\ 2x\ en\ \ x ∈ [-90° ; 90°]\kern2mm\ } $$
[ A 1.18 ]
Die diagramme toon die grafieke van die
trigonometriese funksies wat by elke vraag
gegee word. Gebruik die inligting wat so
gegee word om die waardes van die onbekende
veranderlikes te bepaal :
2.1 Die grafiek van y = a sin k(x + p)
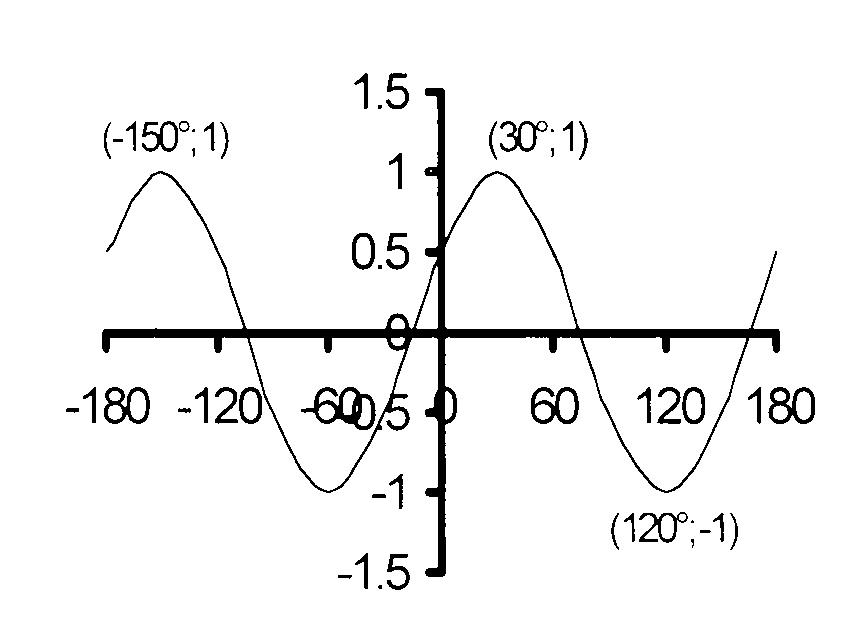 [ A 2.1 ]
2.2
[ A 2.1 ]
2.2 Die grafiek van y = a cos k(x + p)
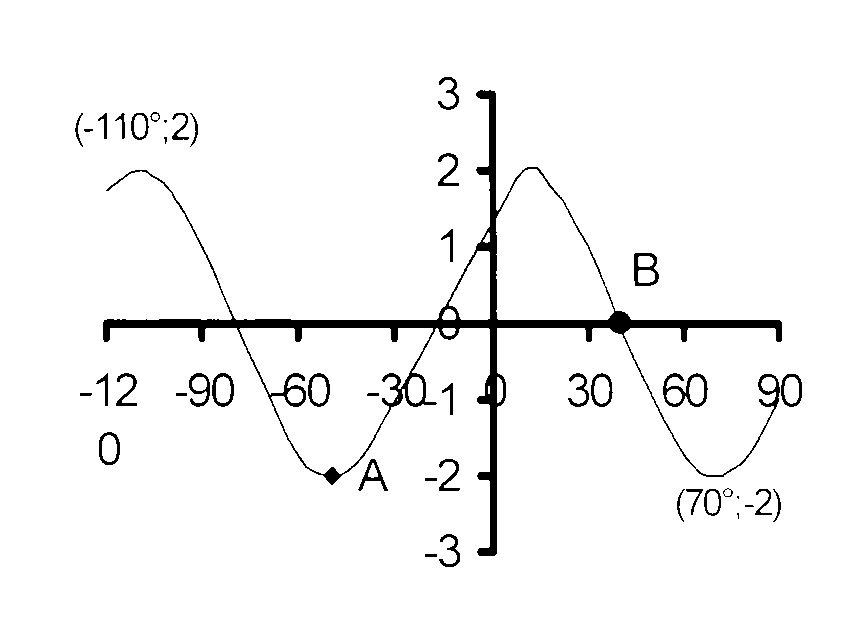 [ A 2.2 ]
2.3
[ A 2.2 ]
2.3 Die grafiek van y = a sin k(x + p)
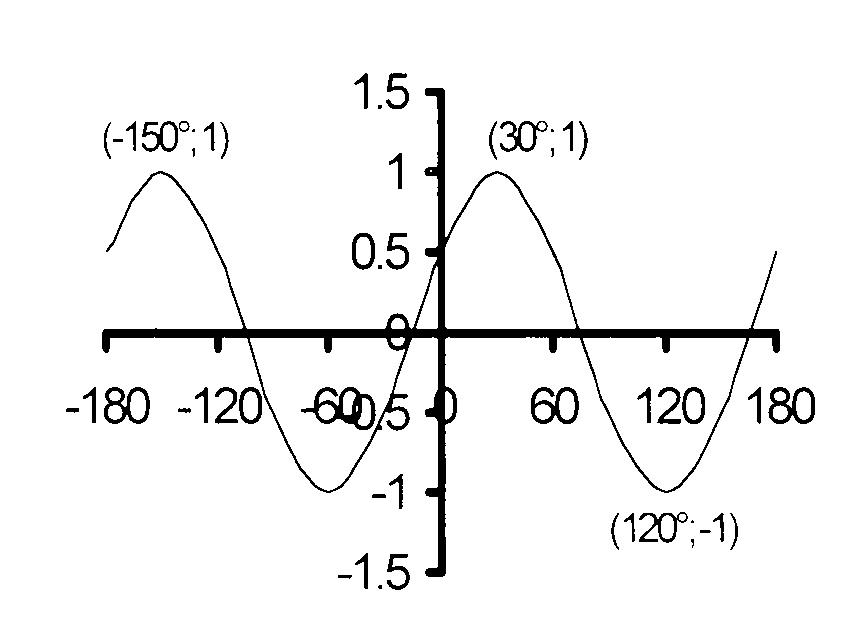 [ A 2.3 ]
2.4
[ A 2.3 ]
2.4 Die grafiek van y = a cos k(x + p)
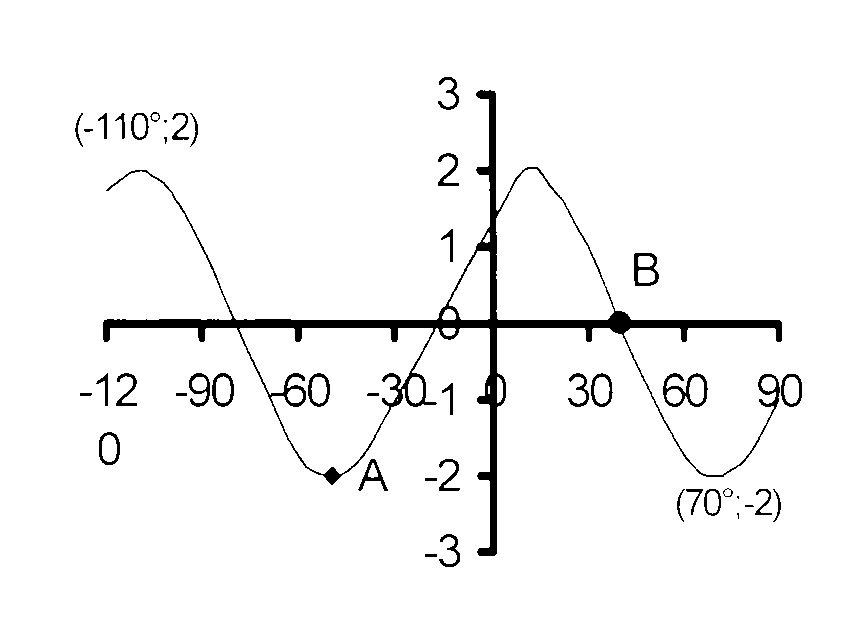 [ A 2.4 ]
2.5
[ A 2.4 ]
2.5 Die grafiek van y = a sin k(x + p)
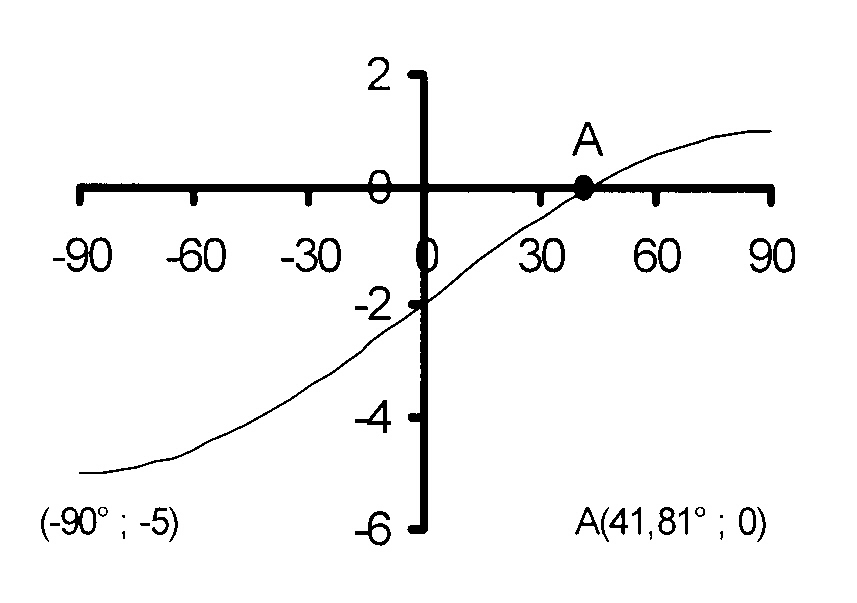 [ A 2.5 ]
2.6
[ A 2.5 ]
2.6 Die grafiek van y = a cos k(x + p)
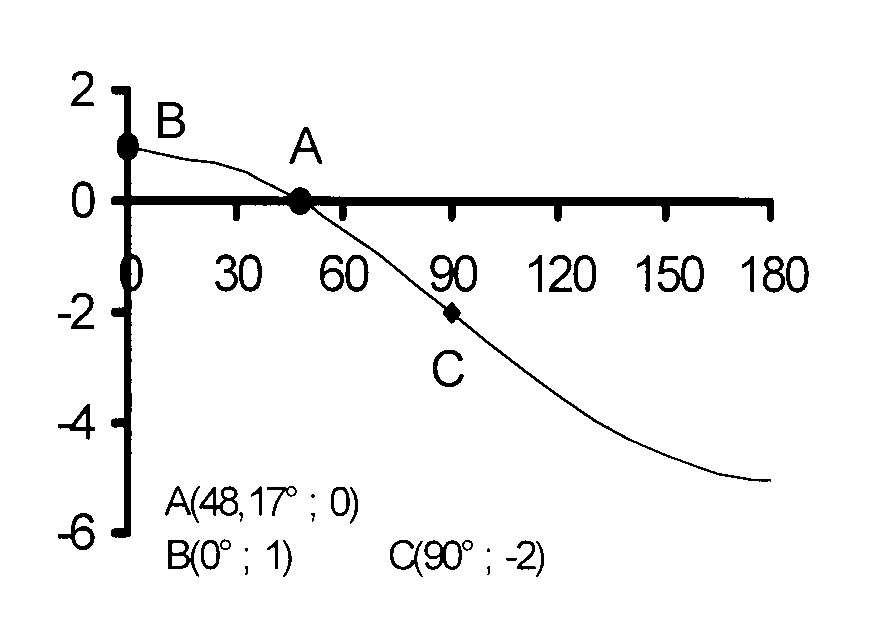 [ A 2.6 ]
[ A 2.6 ]
3.1 Teken op dieselfde assestelsel die
grafieke van f(x) = sin (x − 30°) en
g(x) = cos 2x vir − 180° ≤ x ≤ 180°.
Gee die afsnitte met die asse.
[ A 3.1 ]
3.2 Gee die periode van f.
[ A 3.2 ]
3.3 Bepaal x deur berekening indien
f(x) = g(x).
[ A 3.3 ]
3.4 Vir watter waarde(s) van x
is f(x) < -0,5?
[ A 3.4 ]
3.5 Vir watter waarde(s) van x
sal f(x) ≥ 0,5?
[ A 3.5 ]
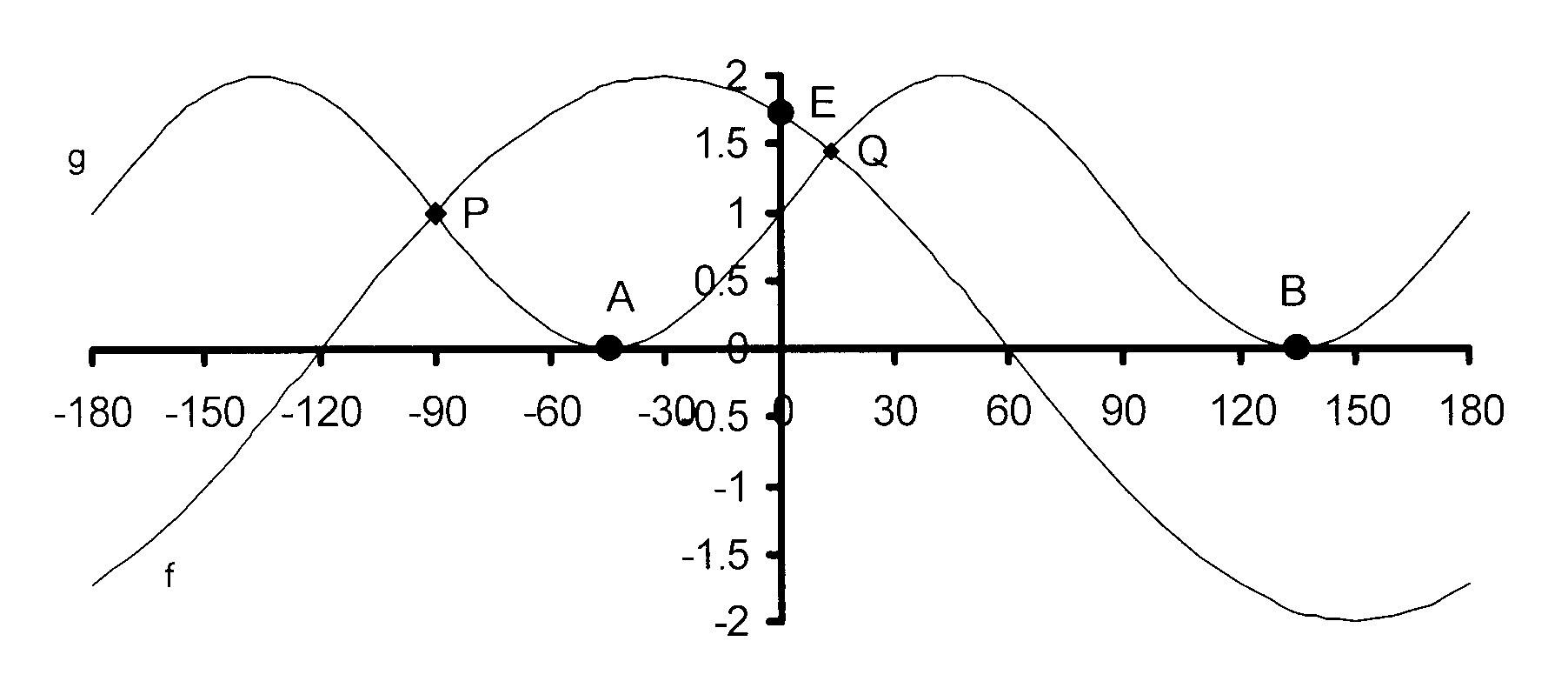
In die diagram word die grafieke van
f(x) = a cos (x + b) en g(x) = c + sin dx vir
−180° ≤ x ≤ 180° getoon.
4.1 Bepaal die waardes van a, b, c en d deur
die grafieke te gebruik.
[ A 4.1 ]
4.2 Bereken die waarde van f(x) as x = 0° sonder
die gebruik van 'n sakrekenaar.
[ A 4.2 ]
4.3 Bepaal x deur die grafieke te gebruik as
4.3.1 g(x) = 2
[ A 4.3.1 ]
4.3.2 f(x) ≥ g(x)
[ A 4.3.2 ]
4.4 Die Y-as word verskuif om deur die
draaipunt van f, waar f(x) 'n
maksimum bereik te gaan.
Bepaal 'n vergelyking vir f in die vorm
y = . . . met verwysing na die
nuwe stel asse.
[ A 4.4 ]
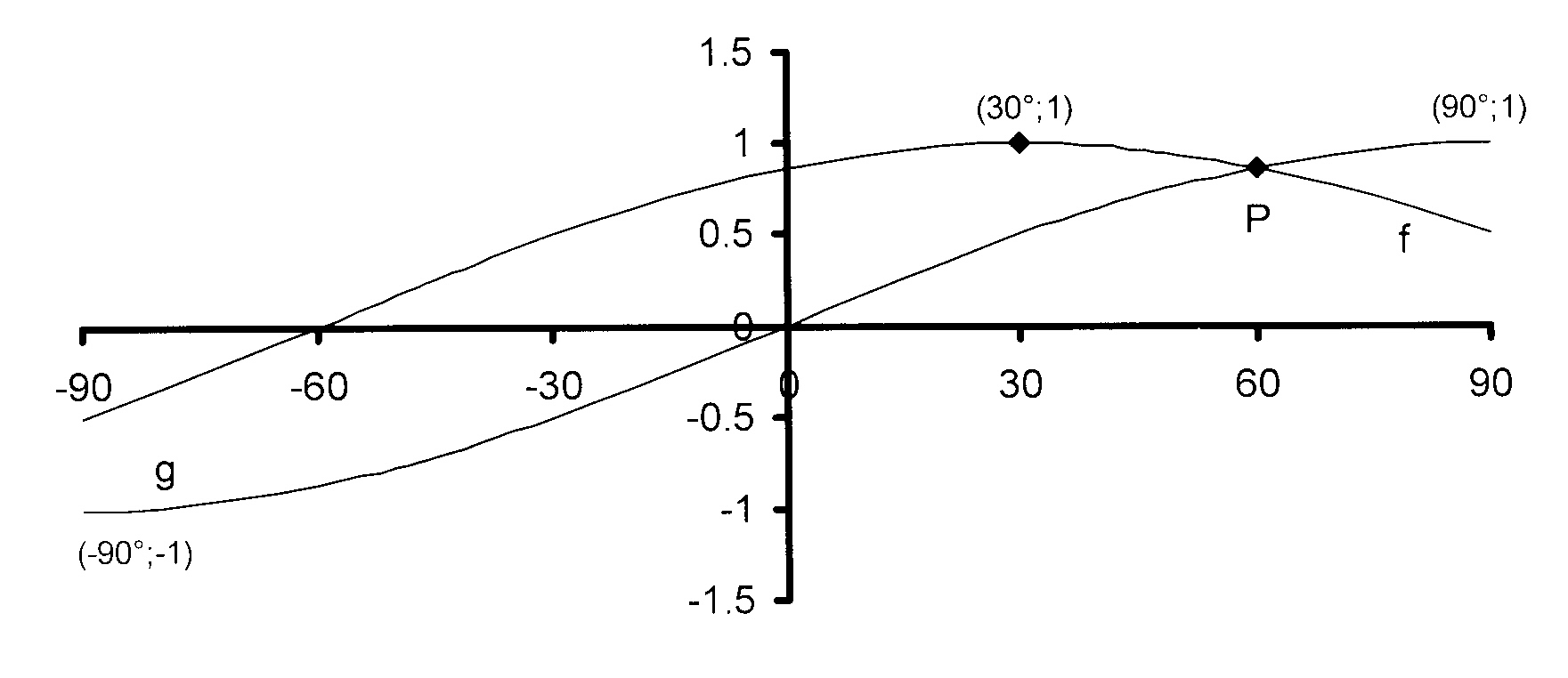
Die diagram toon die grafieke van
f(x) = a cos (x + b) en g(x) = sin cx vir
−90° ≤ x ≤ 90° getoon.
5.1 Bepaal die waardes van a, b en c
deur die grafieke te gebruik.
[ A 5.1 ]
5.2 Gebruik die grafieke om die volgende
vrae te beantwoord :
5.2.1 Skryf die waardeversameling
van f neer.
[ A 5.2.1 ]
5.2.2 Vir watter waardes van x is f(x)
dalend as x toeneem?
[ A 5.2.2 ]
5.2.3 Vir watter waarde(s) van x is
f(x)
.g(x) ≥ 0 as x ∈ [−90° ; 0°]?
[ A 5.2.3 ]
5.3 Los die vergelyking cos (x − 30°) = sin x
op as x ∈ [−90° ; 90°] en skryf
vervolgens die waardes van x in die
interval [−90° ; 90°] neer sodat g(x) > f(x).
[ A 5.3 ]
5.4 Die grafiek van h(x) word gevorm deur
die grafiek van g(x) 60° na links te skuif.
Skryf die vergelyking van h(x) neer.
[ A 5.4 ]
5.5 Hoe kan die grafiek van f(x) verskuif
word om die grafiek van g(x) te vorm?
[ A 5.5 ]
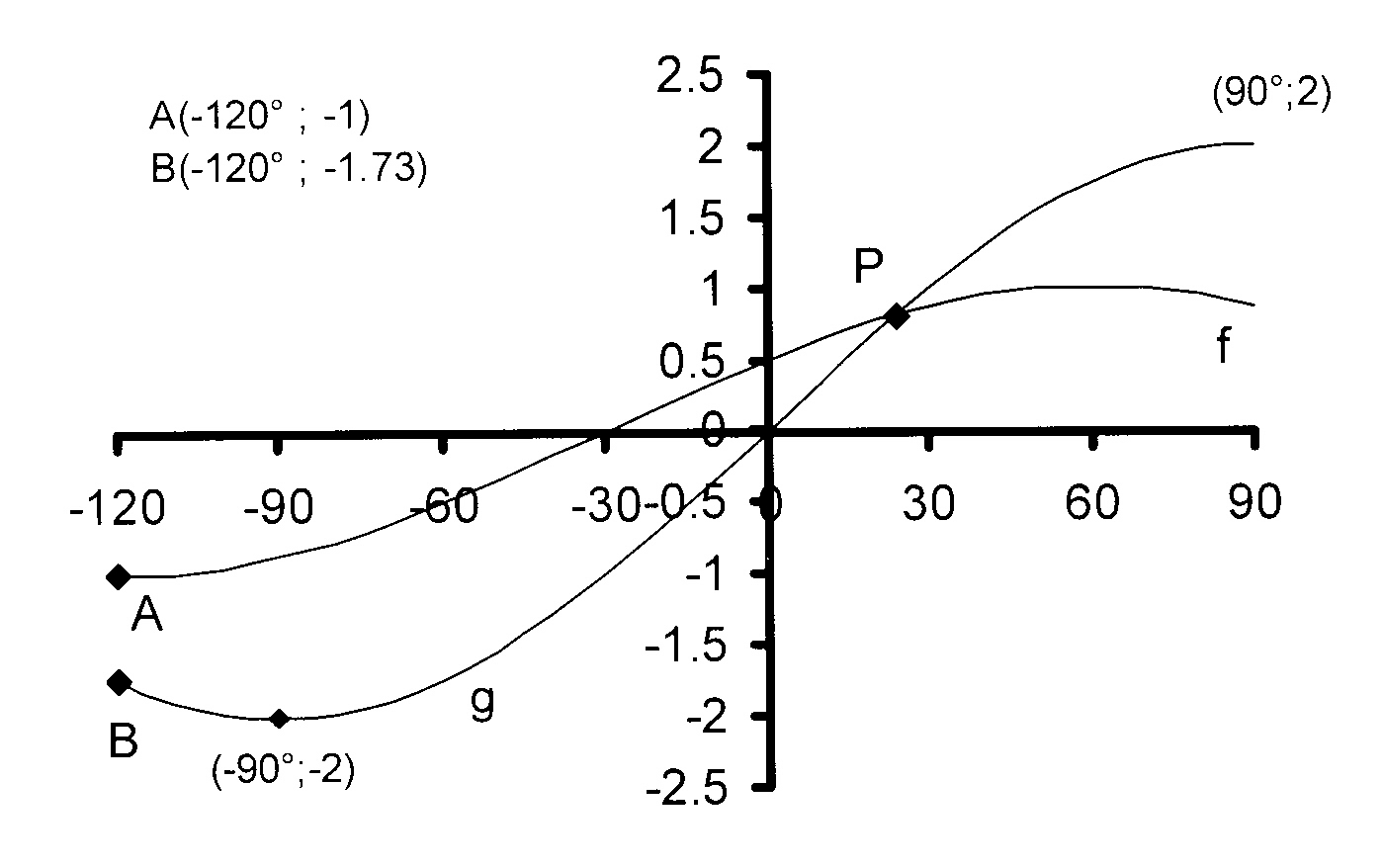
Die diagram vertoon die grafieke van
f(x) = a cos (x + b) en g(x) = c sin dx vir
−120° ≤ x ≤ 90°.
6.1 Skryf die amplitude en periode
van g neer.
[ A 6.1 ]
6.2 Bepaal die waardes van a, b, c
en d.
[ A 6.2 ]
6.3 Skryf die omvang van g neer.
[ A 6.3 ]
6.4 Skryf neer die waarde(s) van x < 0°
waarvoor f(x)
.g(x) ≥ 0.
[ A 6.4 ]
6.5 As die Y-axis na links verskuif word sodat
dit deur die snypunt van die gegewe
kosinus kromme en die X-as gaan,
watter funksie word nou voorgestel
deur die gegewe oorspronklike
sinus funksie?
[ A 6.4 ]
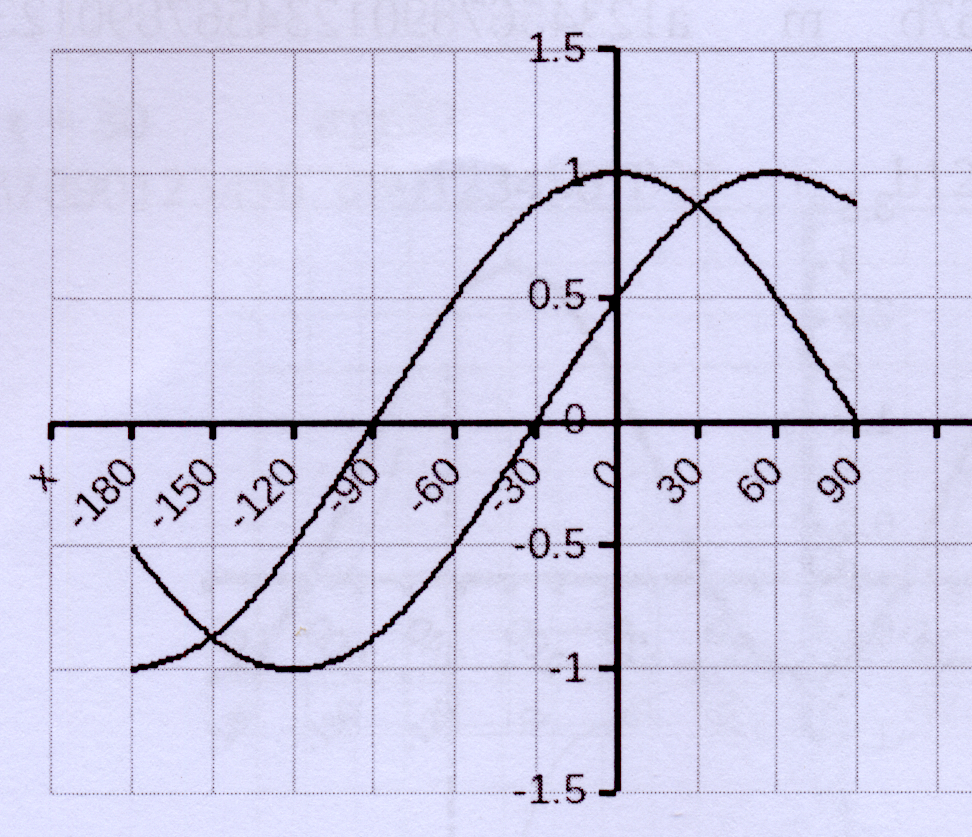
Die diagram stel die grafieke van
f(x) = cos x en g(x) = sin (x + b) vir die
interval −180° ≤ x ≤ 90° voor.
7.1 Skryf b se waarde neer.
[ A 7.1 ]
7.2 Skryf g se periode neer.
[ A 7.2 ]
7.3 Skryf die waarde(s) van x in die
interval − 180° ≤ x ≤ 90° neer
waarvoor f(x) − g(x) = 0
[ A 7.3 ]
7.4 Vir watter waardes van x in die
interval − 180° ≤ x ≤ 90° sal
7.4.1 sin (90° − x) > g(x)?
[ A 7.4.1 ]
7.4.2 f(x)
.g(x) < 0?
[ A 7.4.2 ]
7.4.3 f(x)
.g(x) ≥ 0?
[ A 7.4.3 ]
7.5 Die grafiek van h word verkry deur
f 3 units opwaarts te skuif. Bepaal h se
omvang.
[ A 7.5 ]
7.6 Die grafiek van p is verkry deur
f 3 eenhede afwaarts te skuif.
Skryf p se vergelyking neer.
[ A 7.6 ]
7.7 q se grafiek word verkry deur
f 30° na links te skuif. Skryf q se
vergelyking neer.
[ A 7.7 ]